6.3. Найпростіші квадратурні правила

Прагнення підвищити точність наближеного обчислення інтеграла шляхом підвищення ступеня інтерполяційного багаточлена неминуче приводить до зростання технічних складностей при обчисленні квадратурних коефіцієнтів. Тому на практиці намагаються обійтися багаточленами невисокого ступеня, розбиваючи вихідний відрізок інтегрування на менші частини. У результаті цього одержують сімейства квадратурних правил, що залежать від ступеня використаних інтерполяційних багаточленів. Розглянемо найпростіші з них.

Правило прямокутників. Вихідний відрізок [a,b] розбивається на n рівних частин величиною , на кожному з них вибирають по одній точці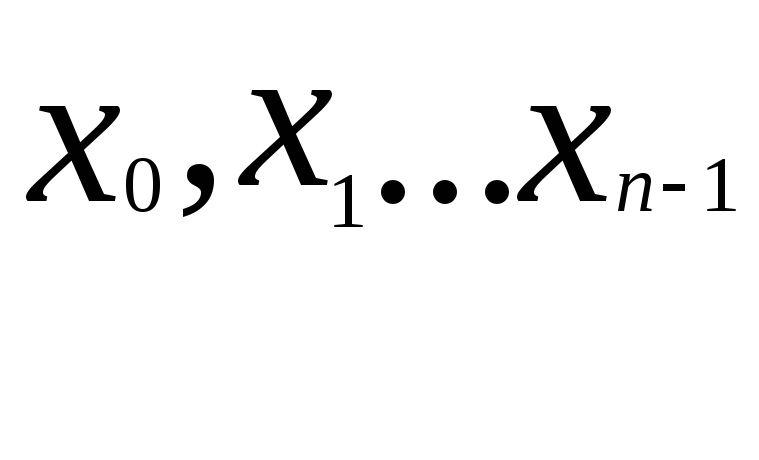. Далі, застосовуючи до кожної з них формулу (4) одержуємо правило

, (8)

називане правилом прямокутників.

Якщо f(x)0, то площа криволінійної трапеції що виражається, згідно (8), обчислюється як площа фігури, що складає із прямокутників з висотою h і висотами . Залежно від вибору точокxi розрізняють формули лівих і правих прямокутників (Малюнок 1).

а)

б)

Малюнок 1. Правило прямокутників : а)- лівих; б)- правих

Правило трапецій. Розділимо відрізок [a, b] на n рівних частин і позначимо точки ділення через =a+ih,, . Застосовуючи, далі, до кожного з відрізків формулу (5), одержимо квадратурне правило

, (9)

називане формулою трапецій. Її геометричний зміст складається в заміні кривій y=f(x) ламаною й заміни криволінійної трапеції, що відповідає промiжку , звичайної, – прямолінійної

Малюнок 2. Правило трапецій

Правило парабол. Розділимо відрізок [a, b] на n =2m частин, позначимо точки ділення через і розглянемо здвоєні відрізки. До кожного з них застосуємо формулу (6), у результаті чого одержимо правило

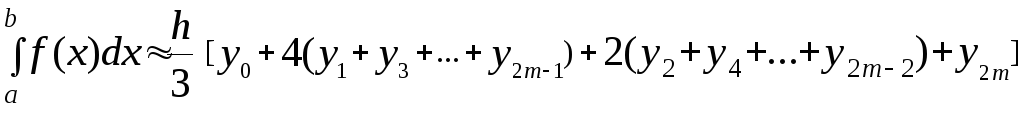, (10)

де , що називаєтьсяформулою парабол або Симпсона. Назва також почасти пояснюється геометричними особливостями, що складаються в тім, що на кожному здвоєному відрізку крива y=f(x) заміняється дільницями параболи.

Правило трьох восьмих. Розділимо вихідний відрізок на 3m частин, утворимо строєні відрізки й до кожного з них застосуємо формулу (7). У результаті цього одержимо правило

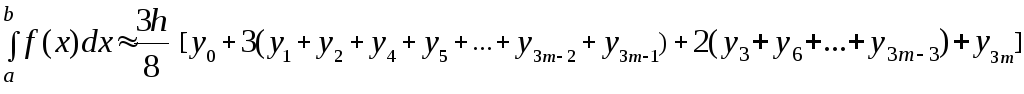, (11)

де , називанеформулою трьох восьмих .

6.4. Погрішності квадратурних формул

Погрішності квадратурних формул, розглянутих у п.3, установлюються схожим образом. А саме, у кожному випадку визначаються локальні погрішності, які потім підсумуються.

Розглянемо формулу лівих прямокутників (8). Відповідно до формули Тейлора погрішність інтерполяційної формули на відрізку становить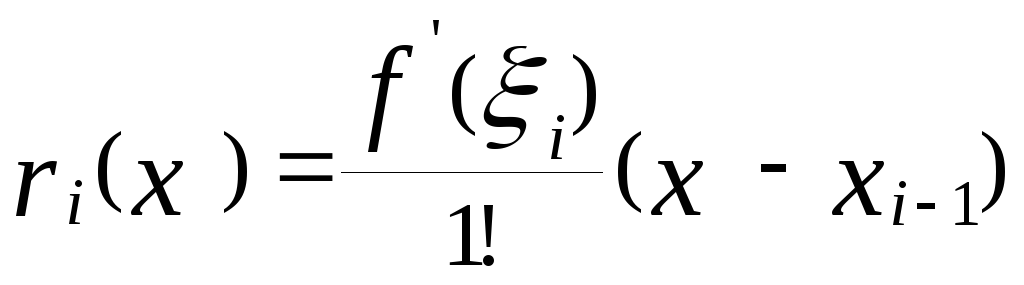,де . Тоді погрішність інтегрування формули виду (4) описується вираженням

,

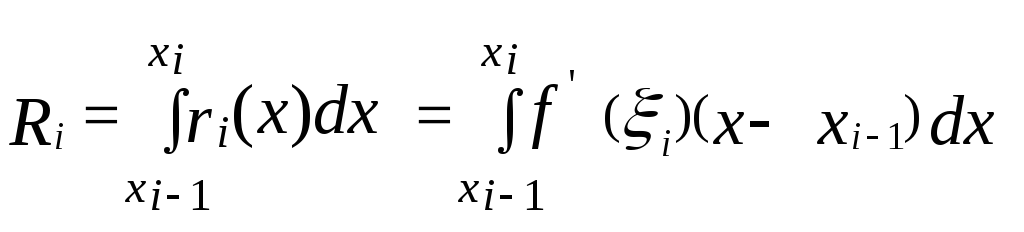яке, відповідно до узагальненої теореми про середнє значення, можна представити в більше зручній для наступного використання формі

,

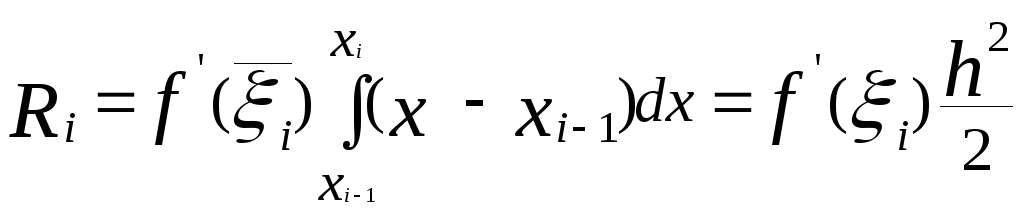де .

Тоді погрішність R формули (8) дорівнює

.

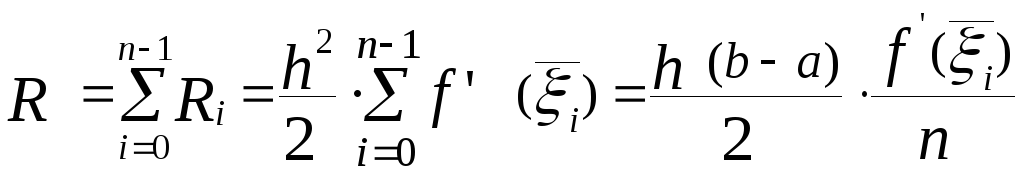Далі, припустимо функцію f(x) безперервно дифференцьована на відрізку [a, b]. Тоді по теоремі Вейерштрасса найдеться значення [a, b] і вираження для опису погрішності приймає остаточний вид

. (12)

Використовуючи (12), можна вибрати крок h і число n, що забезпечують задану точність інтегрування . Дійсно, нехай, тоді

.

Зажадавши

,

одержимо

.

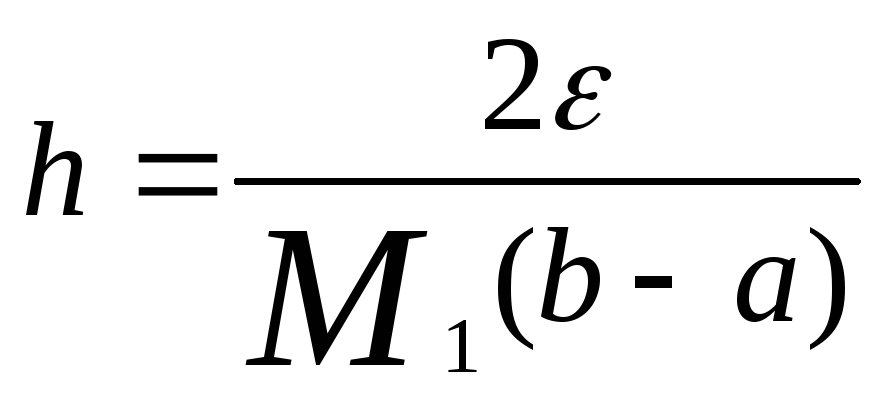Розглянемо формулу трапецій (9).

Визначимо локальну погрішність інтегрування на відрізку [ xi-1, xi]. Погрішність інтерполяції дорівнює

,

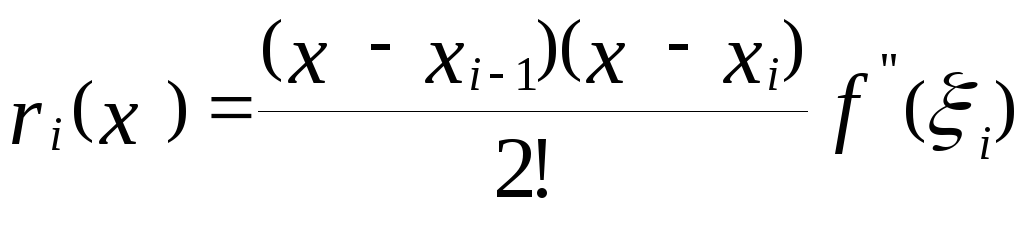де [ xi-1, xi]

Тоді, відповідно до теореми про середнє значення

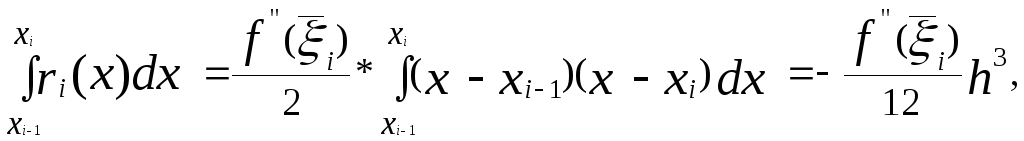
де . Далі, проводячи підсумовування локальних погрішностей, одержимо глобальну, що допускається на відрізку [a, b] при використанні формули трапеції

,

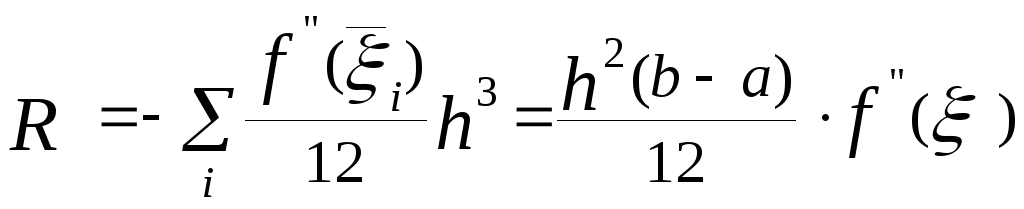де

Проведемо без доказу погрішності

для правила Симпсона,-

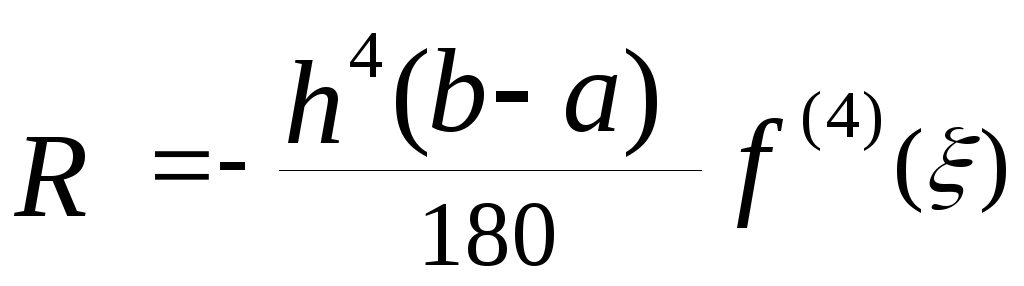
і для правила 3/8, -

.

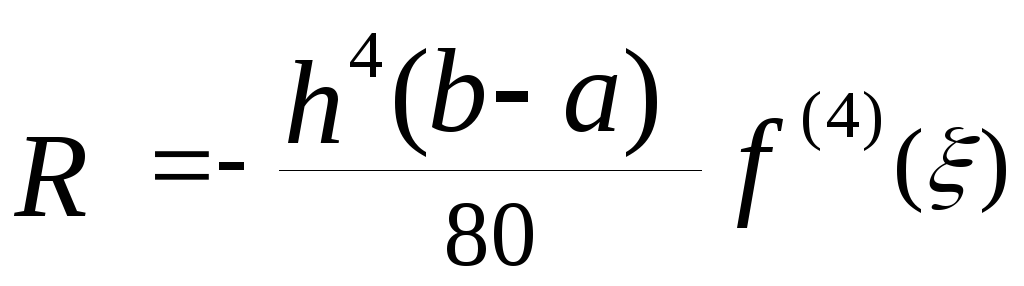Їхнє обґрунтування див. у монографії : Крилов В.И., Бобков, Монастирний. Обчислювальні методи. т2. -М.: Наука, 1977. -400с.

У висновку оборотний увагу на наступний цікавий факт. Незважаючи на більше високий ступінь інтерполяційного багаточлена, використовуваного в правилі 3/8, його підсумкова погрішність інтегрування, за інших рівних умов, вище, ніж у правилі Симпсона.