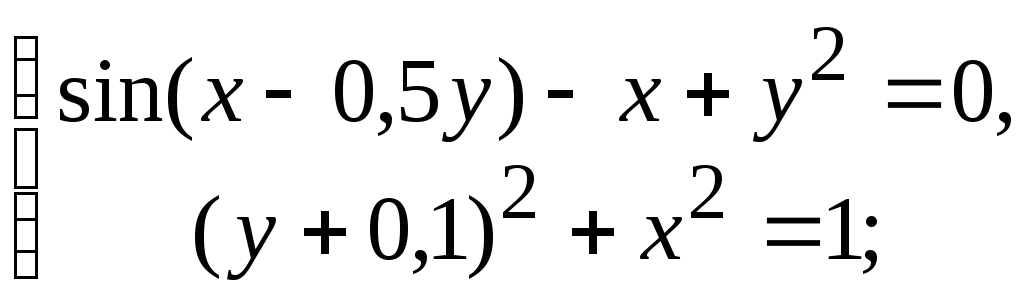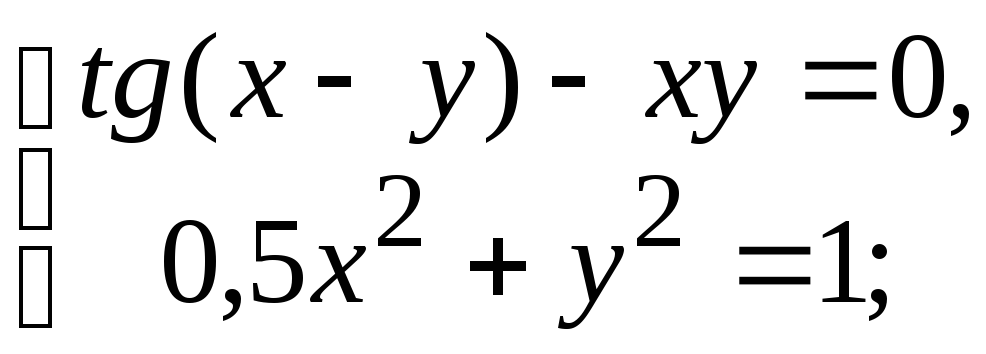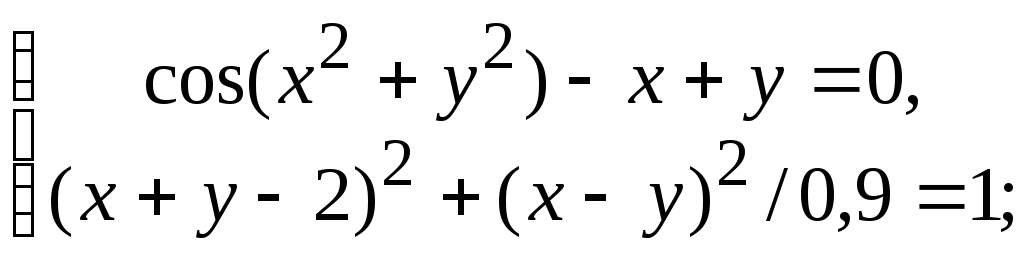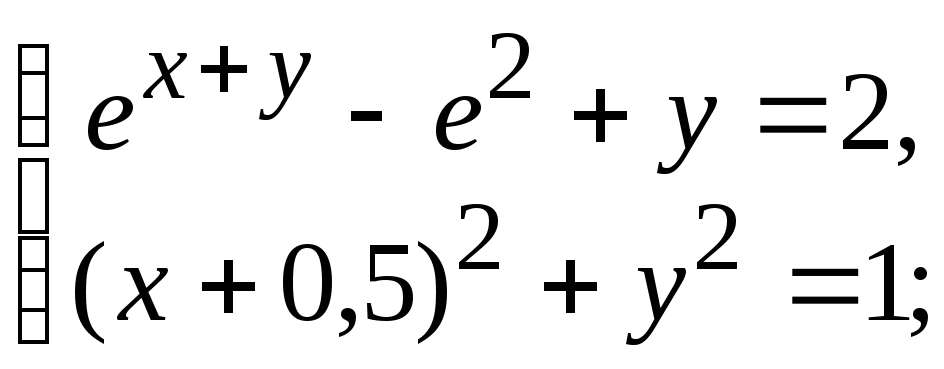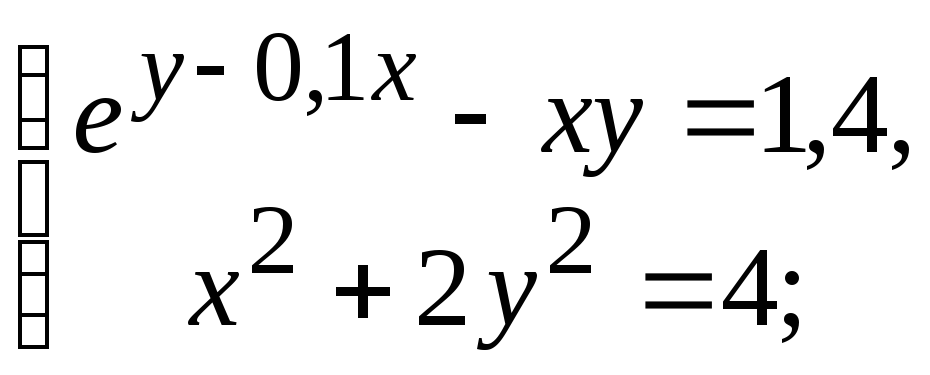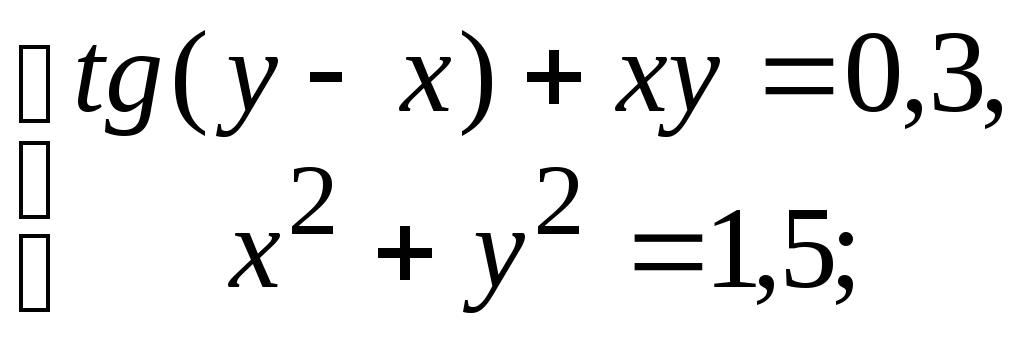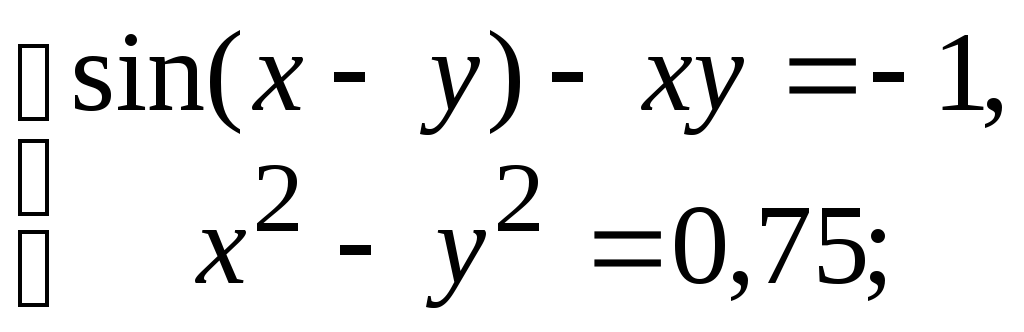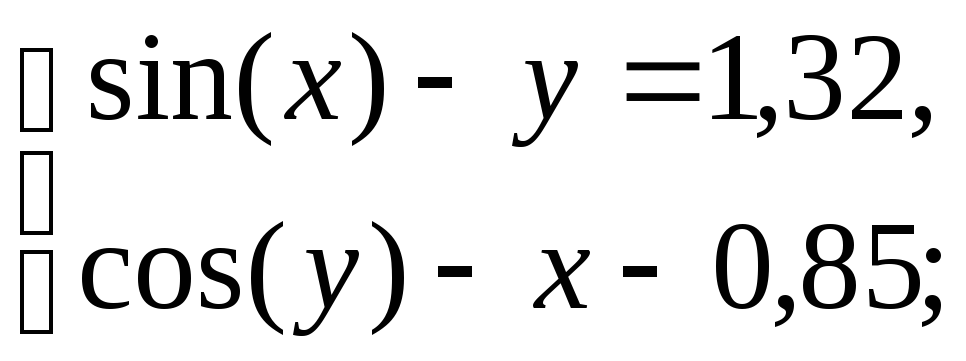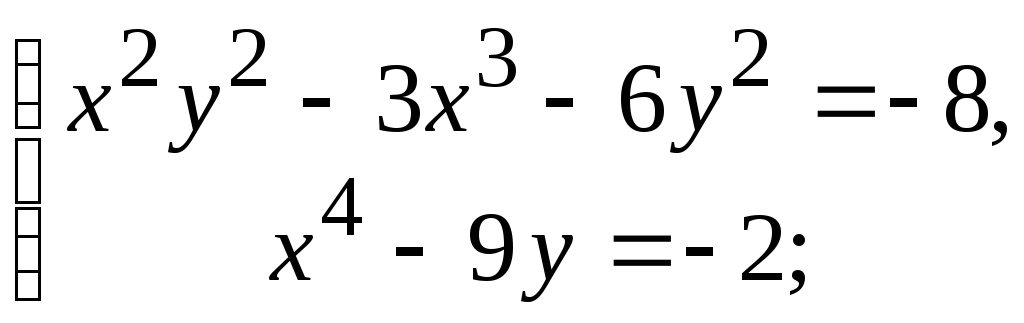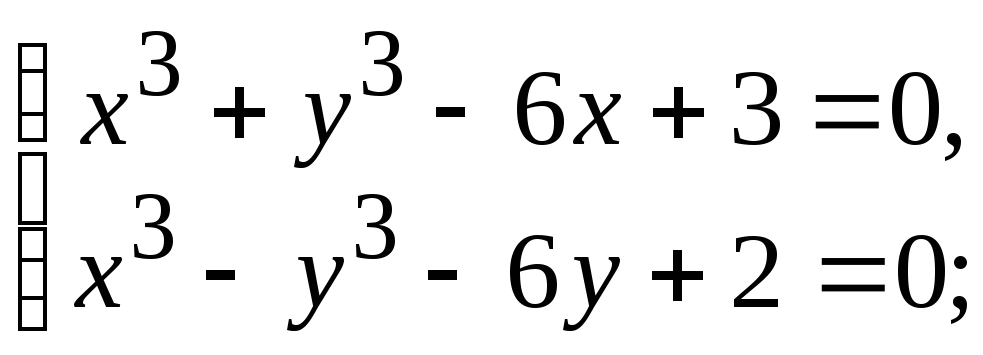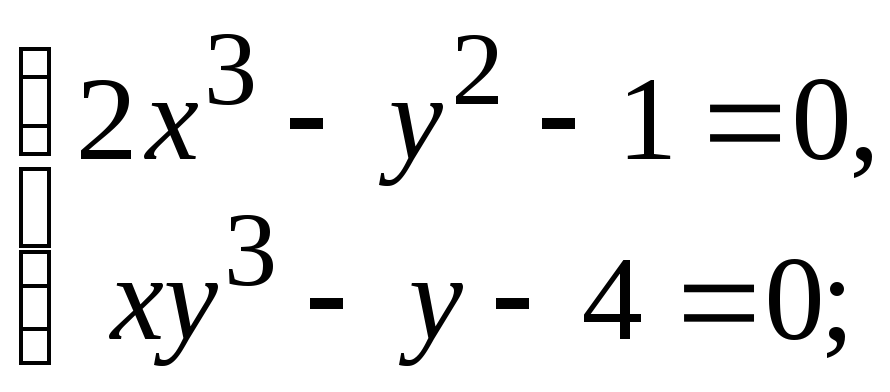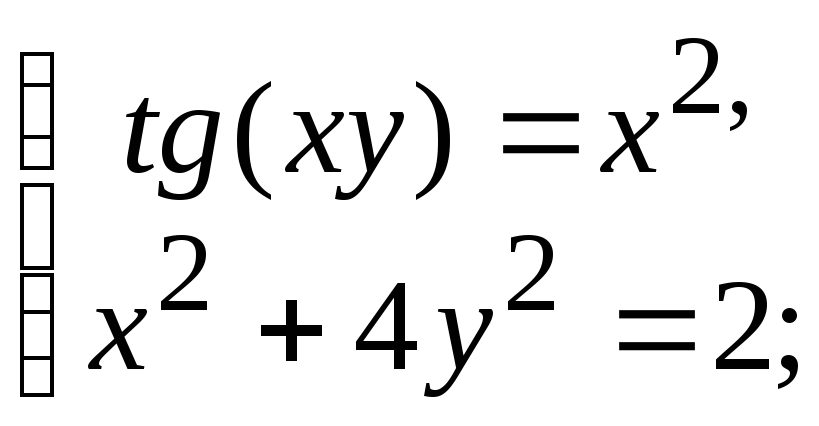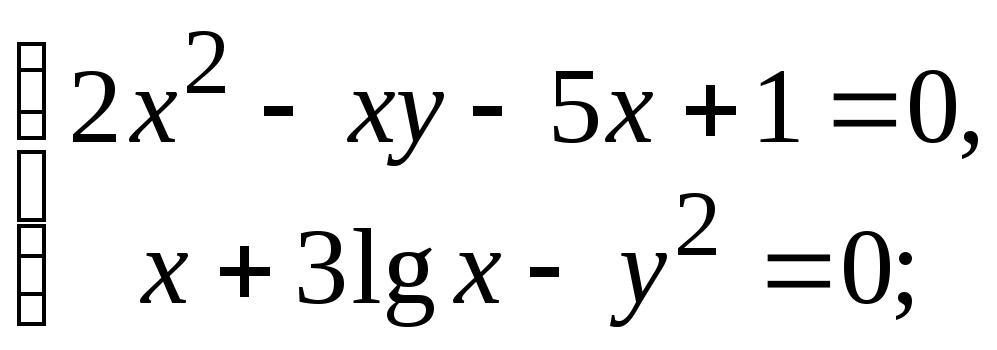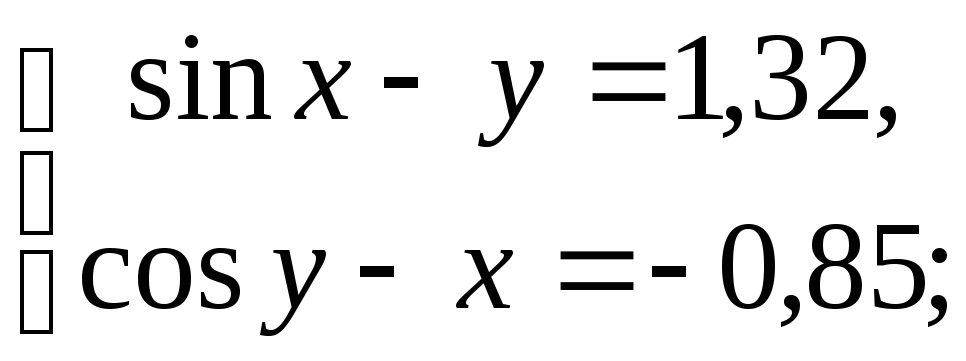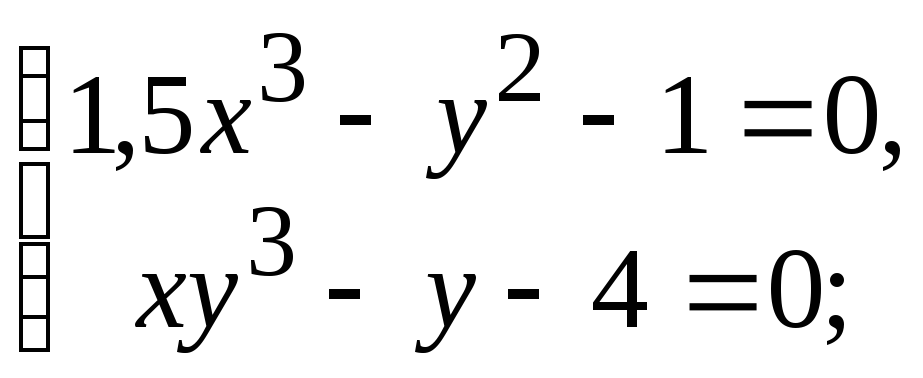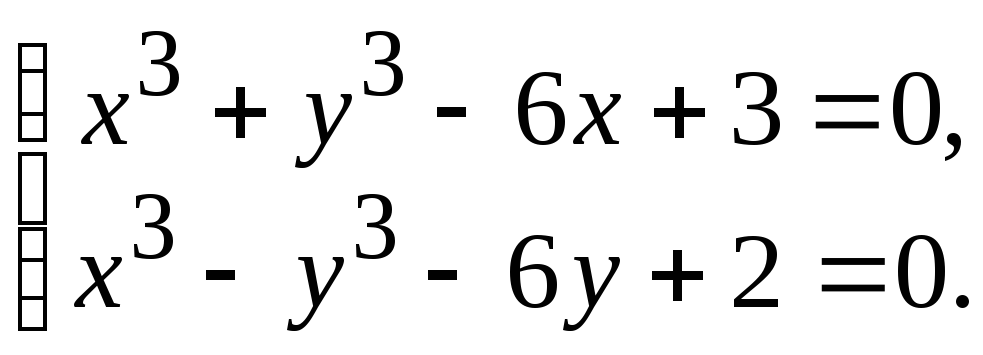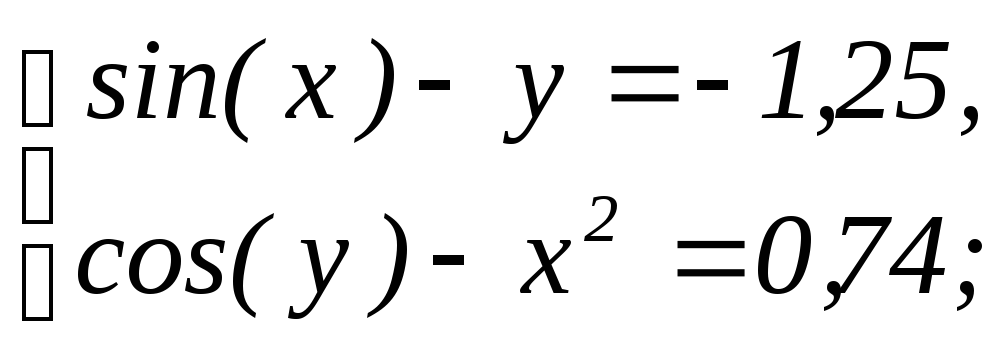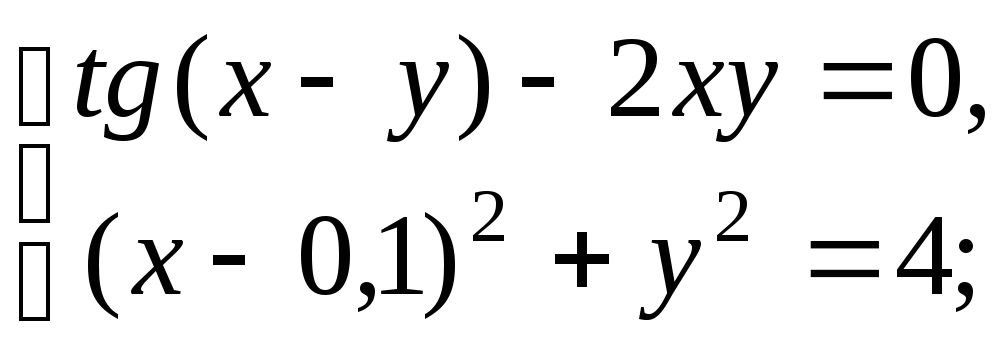- •В. Н. Бєловодський Вісім лекцій по чисельних методах
- •7.080407 «Комп'ютерний еколого-економічний моніторинг»)
- •Лекція 1.Елементи теорії погрішностей
- •.Типи й джерела погрішностей
- •1.2.Абсолютні й відносні погрішності наближених чисел
- •1.3. Погрішності виконання арифметичних операцій
- •.Погрішність обчислення функції
- •1.5.Запис наближених чисел
- •1.6.Правила дій над наближеними числами
- •1.7.Погрішності при машинному поданні чисел
- •1.8. Варіанти індивідуальних завдань
- •Лекція 2. Інтерполяція функцій
- •2.1. Постановка задачі
- •2.2. Алгебраїчна інтерполяція, існування й одиничність інтерполяційного багаточлена
- •2.3. Інтерполяційний багаточлен Лагранжа
- •2.4. Кінцеві й розділені різниці
- •2.5. Інтерполяційний багаточлен Ньютона
- •2.6. Порівняльний аналіз інтерполяційних багаточленів
- •2.7. Погрішності інтерполяційних формул
- •2.8. Інтерполяційні формули для рівновіддалених вузлів
- •2.9. Сплайн - інтерполяція
- •2.10. Варіанти індивідуальних завдань
- •Лекція 3. Методи рішення систем лінійних алгебраїчних рівнянь
- •3.1. Попередні зауваження
- •3.2. Точні методи рішення
- •3.3. Наближені методи рішення
- •3.4. Збіжність і погрішність наближених методів
- •3.6. Варіанти індивідуальних завдань
- •Лекція 4. Вирішення нелінійних рівнянь
- •4.1. Попередні зауваження
- •4.2. Методи, засновані на алгебраїчній інтерполяції
- •4.3. Метод послідовних наближень
- •4.4. Завдання
- •Лекція 5. Рішення систем нелінійних рівнянь
- •Метод ітерацій
- •Метод Ньютона
- •5.3. Порівняльний аналіз методів
- •5.4. Завдання
- •Вимоги до програми
- •Вимоги до звіту
- •6.1. Вступні зауваження
- •6.2. Формули Ньютона-Котеса
- •6.3. Найпростіші квадратурні правила
- •6.4. Погрішності квадратурних формул
- •6.5. Поняття про методи Монте-Карло
- •6.6. Завдання
- •Варіанти завдань
- •Лекція 7. Методи рішення звичайних диференціальних рівнянь
- •Вступні зауваження
- •Аналітичні методи
- •Чисельні методи рішення. Правило Рунге
- •Завдання
- •Лекція 8. Основи спектрального аналізу
- •Елементи загальної теорії
- •Дискретна форма рядів Фур'є
- •8.4. Завдання
Вимоги до звіту
Звіт повинен містити наступні обов'язкові пункти:
титульний лист установленого зразка;
формулювання завдання;
короткі теоретичні відомості про застосовувані методи;
графіки функцій;
результати розрахунків: ручного й за допомогою програми;
текст програми;
висновки.
Варіанти до завдання
Лекція 6. .Наближене обчислення визначених інтегралів
У якій формулюються основні ідеї, реалізовані при наближеному обчисленні визначених інтегралів, розглянуті найпростіші квадратурні формули для рівновіддалених вузлів, обговорюються питання погрішності. Дано поняття про методи Монте-Карло.
6.1. Вступні зауваження
Нижче розглядаються методи наближеного інтегрування власних інтегралів Римана
![]() . (1)
. (1)
Традиційний підхід полягає в наступному.
На
відрізку [a,
b]
вибирається ряд вузлових точок
![]() і
значення інтеграла представляється у
вигляді лінійної комбінації значень
функції ,що знаходиться під iнтегралом,
у вузлових точках
і
значення інтеграла представляється у
вигляді лінійної комбінації значень
функції ,що знаходиться під iнтегралом,
у вузлових точках
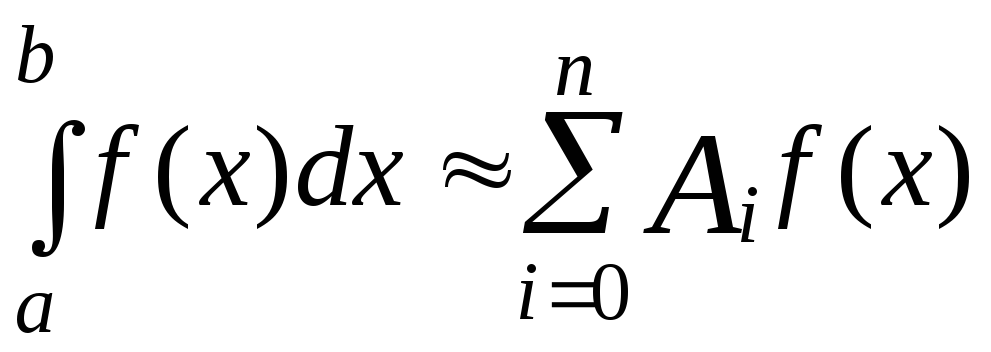 ,
,
яка
називається квадратурною
формулою.
При заданому числі n розташування вузлів
і значення коефіцієнтів
![]() підбирається так, щоб забезпечувалася
найвища точність результату. Найбільш
прості й уживані методи, у яких вузлові
точки вибираються рівновіддаленими.
На їхньому розгляді далі ми й зупинимося.
підбирається так, щоб забезпечувалася
найвища точність результату. Найбільш
прості й уживані методи, у яких вузлові
точки вибираються рівновіддаленими.
На їхньому розгляді далі ми й зупинимося.
6.2. Формули Ньютона-Котеса
Припустимо,
що відрізок [a,
b]
розділений
на n
рівних частин величиною
![]() й позначимо точки ділення через
й позначимо точки ділення через![]() .
Представимо функціюf(x)
за допомогою багаточлена Лагранжа
.
Представимо функціюf(x)
за допомогою багаточлена Лагранжа
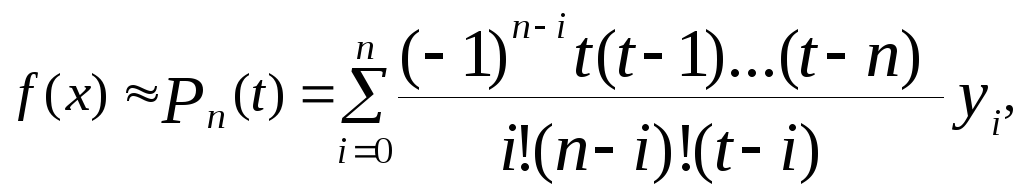
де t =
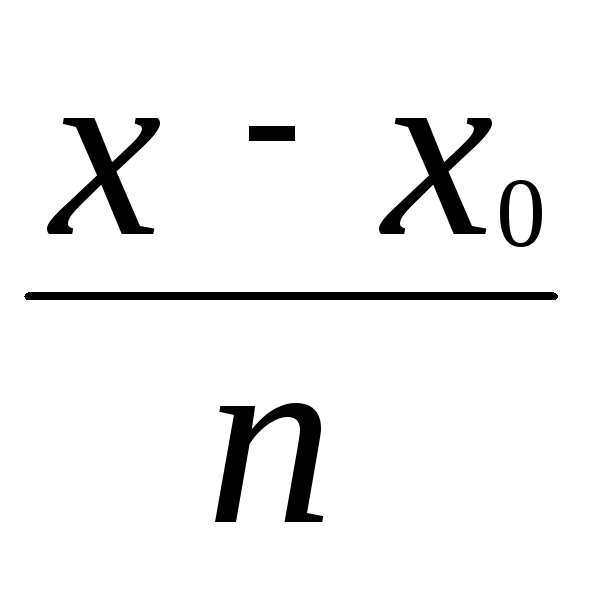 .
.
Тоді
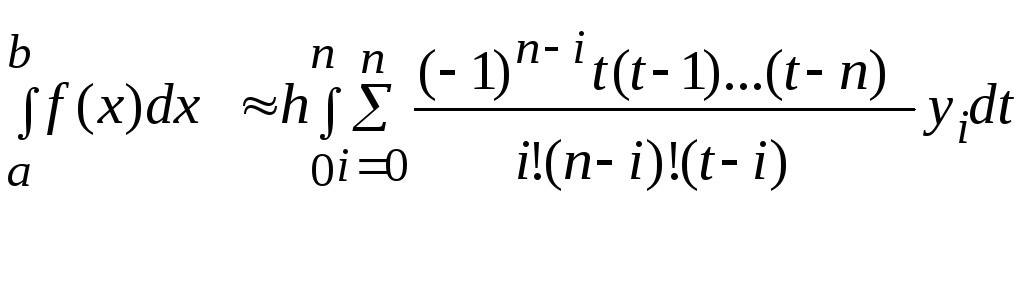 (2)
(2)
або
 ,
,
де
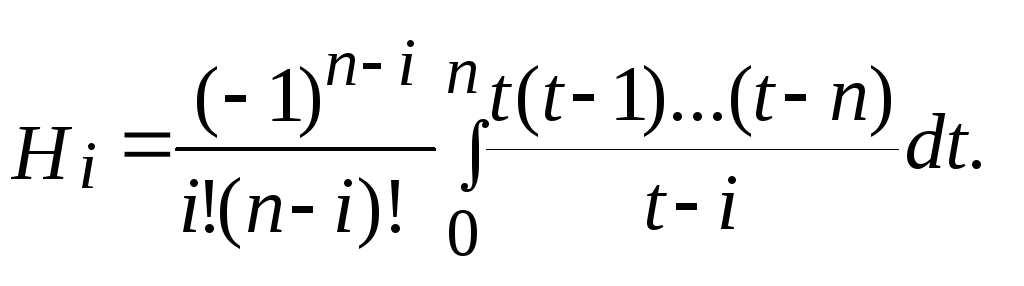 (3)
(3)
Співвідношення
(2),
(![]() )і
називаються квадратурними
формулами Ньютона-Котеса.
)і
називаються квадратурними
формулами Ньютона-Котеса.
У випадку,
коли ділення відрізка [a,b]
не виконується й на ньому вибирається
єдина вузлова точка, позначимо її через
![]() ,
інтерполяційний багаточлен приймає
вид
,
інтерполяційний багаточлен приймає
вид![]() ,
а квадратурна формула, –
,
а квадратурна формула, –
![]() .
(4)
.
(4)
Розглянемо інші найпростіші випадки, попередньо обґрунтувавши важливе, для обчислення коефіцієнтів Hi, властивість:
При
фіксованому n значення Hi
і Hn-i,
де
![]() ,рівні.
,рівні.
Доказ.
Нехай n=2m.
Не применшуючи спільності можна вважати,
що
![]() .
Розглянемо чисельник функції що
знаходиться підiнтегралом
зі співвідношення (2)
.
Розглянемо чисельник функції що
знаходиться підiнтегралом
зі співвідношення (2)
![]() (t)=t(
t-1)…(t-i)…(t-m)…(t-(2m-i))…(t-2m)...
(t)=t(
t-1)…(t-i)…(t-m)…(t-(2m-i))…(t-2m)...
Видалимо
з![]() (t)
множники (
t-i) і ( t-t-(2 m-i)) і
позначимо добуток що залишилися , –
через
(t)
множники (
t-i) і ( t-t-(2 m-i)) і
позначимо добуток що залишилися , –
через
![]() .
Т.е.
.
Т.е.
![]() (t)=(
t-i) ( t-t-(2 m-i))
(t)=(
t-i) ( t-t-(2 m-i))
![]() (t).
(t).
Тоді
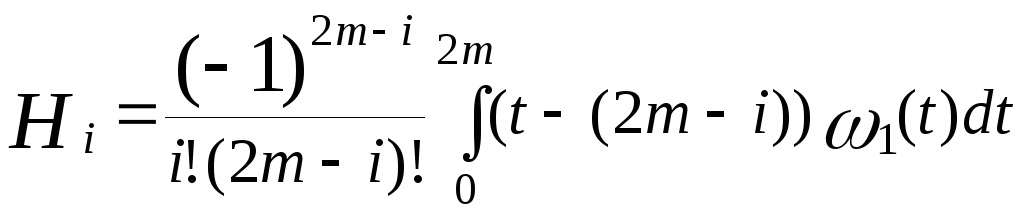
та
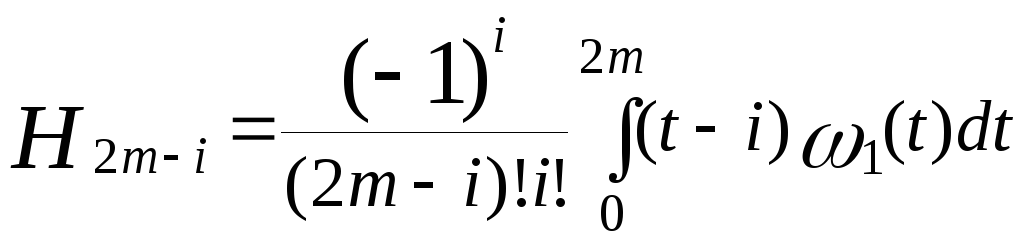
Зробимо в останніх інтегралах заміну t-m=z або t=z+m. Тоді
![]()
і є
непарною функцією змінної z. Вираження
для визначення
![]() ,
,
![]() після очевидних перетворень приймуть
вид
після очевидних перетворень приймуть
вид
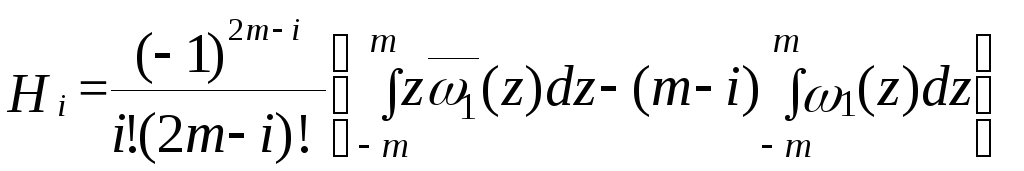 ,
,
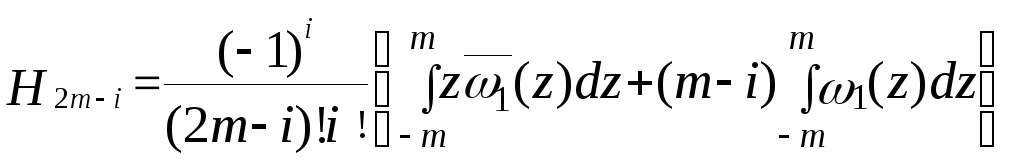 .
.
Другі
доданки у фігурних дужках, у силу
непарності
![]() (z),
рівні 0, а числа2
m-i і
i
мають
однакову парність. Тому
(z),
рівні 0, а числа2
m-i і
i
мають
однакову парність. Тому
![]() ,
що й було потрібно.
,
що й було потрібно.
Випадок n=2m + 1 розглядається аналогічно.
Повернемося
до обчислення коефіцієнтів
![]() .
.
Розглянемо n=1. Тоді з (3) треба
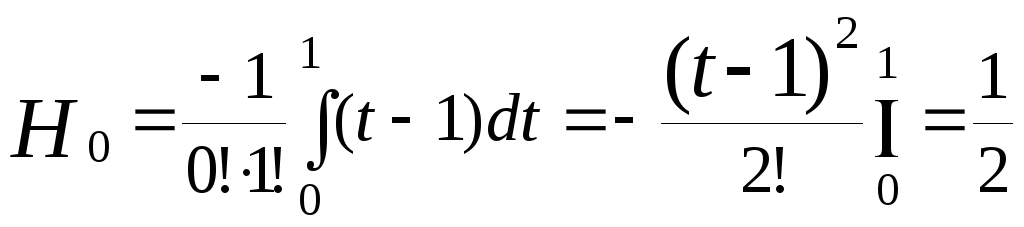 .
.
Звідси
![]() й квадратурна формула (2) приймає вид
й квадратурна формула (2) приймає вид
![]() (5)
(5)
Нехай тепер n=2 З (3) маємо
![]() ,
,
![]() .
.
Тоді
![]() =
=![]() =
=![]()
и
![]() (6)
(6)
Розглянемо n=3. Згідно (3)
![]() ,
,
отже, і
![]() ,
,
 ,
,
отже, і
![]() .
.
Тоді квадратурна формула (2) приймає вид
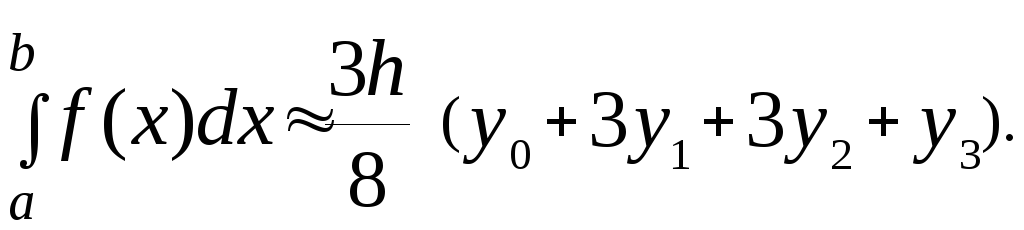 (7)
(7)