5. СреднИе величиНы

6.1. Сущность средних величин

Вариационные ряды отражают большое разнообразие явлений и процессов, составляющих сущность нашей действительности. Для более полного, углубленного их изучения нередко пользуются какой-то одной величиной, которая «впитывает» в себя все особенности данного ряда распределения, основные свойства изучаемой совокупности в отношении определенного признака. Это означает, что для каждого признака статистической совокупности необходимо иметь сводную, сжатую, обобщённую характеристику. Такое возможно при условии, если исчислена средняя величина.

Средняя величина – это обобщенная количественная характеристика признака в статистической совокупности. Она выражает типичное значение признака для всех единиц совокупности под влиянием всего комплекса факторов. В ней погашаются индивидуальные различия единиц совокупности в вариантах осредняемого признака.

Средняя величина – важнейшая категория статистической науки и форма обобщающих показателей. Многие явления и процессы становятся ясными, определенными, лишь будучи обобщенными в форме средних величин. Таковы, например, средняя урожайность, продуктивность животных, производительность труда, себестоимость единицы продукции, заработная плата, душевой доход и т.д.

Основное условие правильного применения средних величин – качественная однородность статистической совокупности. Средние, вычисленные для качественно неоднородной совокупности, теряют свое научное значение. Такие средние являются фиктивными, причем не только не дающими представления о действительности, но искажающими ее и вводящими в заблуждение, так как они стирают существенные различия между явлениями. Например, для характеристики среднего уровня зарплаты в сельскохозяйственной сфере АПК показатель среднего заработка в целом по экономике совершенно непригоден, так как последний в 2-3 раза выше.

Средняя величина независимо от ее вида получает следующее общее выражение:

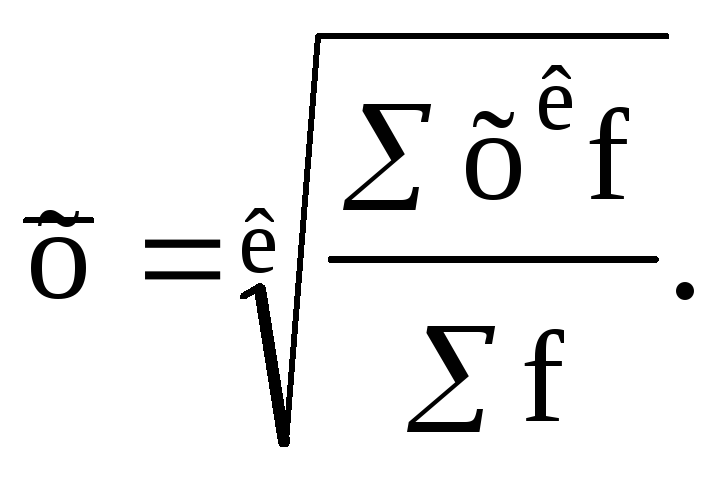(6.1)

Выражение (6.1) принято называть общей формулой средних величин. При разных значениях к формула (6.1) приводит к разнообразным видам средних величин.

Величина к может принимать любое из бесконечных чисел значение. Именно поэтому для каждого признака теоретически может быть рассчитано бесконечное число видов средних величин. Практически же в статистике находит применение не более десяти видов.

Каждый вид средних величин обычно имеет две формы: простую (невзвешенную) и взвешенную. Форма средних зависит от вида вариационного ряда. Так, при расчете средних по несгруппированным данным применяют простую (невзвешенную) форму; в дискретных или интервальных рядах распределения – взвешенную.

6.2. Средняя арифметическая величина

Если в формулу (6.1) подставить значение к=1, то получается средняя арифметическая величина, т.е.

. (6.2)

Поскольку в ранжированном ряду при всех вариантах f=1, то в этом случае применяется средняя арифметическая невзвешенная (простая) величина, т.е.

, (6.3)

где n – число единиц в статистической совокупности.

Расчет средней арифметической простой можно показать на примере ранжированного ряда, составленного по площади посева льна-долгунца в 20 сельскохозяйственных организациях района (табл. 6.1.).

Т а б л и ц а 6.1. Расчет средней арифметической простой в ранжированном ряду распределения

Ранговые №№	Варианты (значения признака)
	Символы	Посевная площадь, га
1	х1	20
2	х2	25
3	х3	30
…	…	…
n	хn	100
Σ	Σх	1200

Подставив данные табл. 6.1 в формулу (6.3), получаем среднее арифметическое простое значение посевной площади льна-долгунца, приходящейся на 1 хозяйство:

.

Поскольку в дискретном ряду распределения каждая варианта представлена определенной локальной частотой (частостью), то среднее значение для каждого такого ряда можно рассчитать по формуле средней арифметической взвешенной, т.е.

, (6.4)

где х – варианты (значение признака); f – локальные частоты (частости).

Определение средней арифметической взвешенной величины можно показать на примере расчёта средней урожайности льносоломки в 20 сельскохозяйственных организациях района (табл. 6.2.).

Т а б л и ц а 6.2. Расчет средней арифметической взвешенной в дискретном ряду распределения

№ п.п.	Варианты		Локальные частоты		Взвешенные средние варианты
	Символы	Урожайность, ц/га	Символы	Посевная площадь, га	Символы	Валовой сбор, т
	х		f		xf
1	х1	50	f1	20	х1f1	100
2	х2	40	f2	25	х2f2	100
3	х3	60	f3	30	х3f3	180
	…	..	…	…	…	…
n	хn	40	fn	100	хnfn	400
Σ			Σ f	1200	Σ xf	6000

Подставив в формулу (6.4) данные табл. 6.2, можно рассчитать среднюю арифметическую взвешенную величину для дискретного ряда распределения:

Таким образом, средняя урожайность, взвешенная по посевной площади льна-долгунца, в сельскохозяйственных организациях района, составила 50 ц/га льносоломки.

Принцип расчёта средней величины в интервальном вариационном ряду аналогичен расчёту среднего значения признака для дискретного ряда (формула 6.4); различия состоят лишь в некоторых деталях.

При вычислении среднего значения признака в интервальном ряду распределения, когда в столбце вариант имеется не одно, а два значения, показывающие нижнюю и верхнюю границы интервала, прежде всего целесообразно найти его срединное значение, т.е. центр интервала, который определяется как простая средняя арифметическая из нижней и верхней варианты каждого интервала, или как их полусумма. Порядок расчёта средней арифметической взвешенной для интервального вариационного ряда по урожайности льносоломки в сельхозорганизациях с закрытыми интервалами показан в табл. 6.3.

Т а б л и ц а 6.3. Расчёт средней взвешенной варианты в интервальном ряду

распределения по урожайности льносоломки

№ п.п.	Интервалы по урожайности, ц/га	Локальные частоты		Средние варианты интервалов		Взвешенные средние варианты
		Символы	Посевная площадь, га	Символы	Урожайность, ц/га	Символы	Валовой сбор, т
		f		х		xf
1	30-40	f1	300	х1	35	Х1f1	1050
2	40-50	f2	400	х2	45	X2f2	1800
3	50-60	f3	300	х3	55	X3f3	1650
4	60-70	F4	200	х4	65	X4f4	1300
Σ	Итого	Σf	1200	-	-	Σ xf	5800

Для нахождения среднего значения признака в интервальном ряду распределения необходимые данные, приведённые в табл. 6.3, подставим в формулу (6.4), получим:

Это означает, что средняя урожайность льносоломки в сельскохозяйственных организациях района составляет 48,3 ц/га.

Если интервальный ряд, используемый для вычисления средней варианты, содержит открытые интервалы, то центры этих интервалов могут быть рассчитаны исходя из предположения, что размеры открытых интервалов совпадают с размерами последующих или предыдущих интервалов, непосредственно к ним примыкающих. При этом срединное значение первого (верхнего) открытого интервала может быть найдено путем вычитания из середины второго интервала величины этого интервала, а срединное значение последнего (нижнего) открытого интервала – прибавлением к середине предпоследнего интервала величины этого же интервала.

Необходимо иметь в виду, что исчисление средней арифметической величины по данным интервального ряда распределения не всегда является абсолютно правильным. Это объясняется неравномерным распределением вариант внутри интервала, в качестве же множителя х для каждого интервала используется его середина. Кроме того, при наличии открытых интервалов к этому добавляются неточности, связанные с установлением неизвестных границ. Поэтому рассмотренный способ расчёта средней варианты для интервального ряда целесообразно применять лишь в тех случаях, когда отсутствуют данные о значениях признака для всей совокупности в целом. При наличии же таких данных точное значение средней варианты может быть получено способом расчёта для дискретного ряда распределения.

В системе АПК средняя арифметическая величина (простая и взвешенная) широко применяется при расчёте многочисленных средних показателей, характеризующих наличие и использование производственного потенциала: средней площади землепользования, посевной площади, урожайности, поголовья, продуктивности животных, численности работников, производительности труда, себестоимости продукции, уровня рентабельности и многих других показателей.