6.5. Средняя квадратическая величина

При условии подстановки значения к=2 в формулу (6.1.) получаем среднюю квадратическую величину. В ранжированном ряду средняя квадратическая величина рассчитывается по невзвешенной (простой) форме:

(6.6)

где х – варианты ранжированного ряда; n – общее число вариант.

Взвешенная форма средней квадратической величины, которая используется для дискретного или интервального ряда, выражается следующим образом:

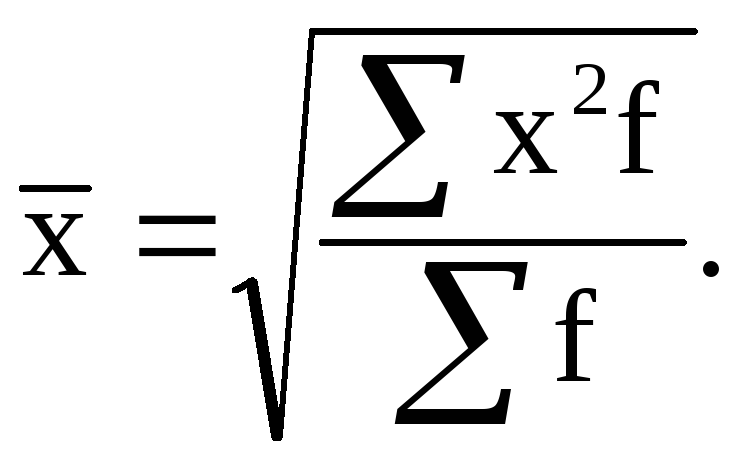(6.7)

Средняя квадратическая величина, как самостоятельный вид средних, имеет ограниченное применение. Допустим, две нестандартные цилиндрические емкости для хранения нефтепродуктов с диаметрами оснований 2 и 5 м необходимо заменить двумя новыми, равными по объему емкостями с одинаковым в основании диаметром. При расчёте среднего диаметра оснований новых емкостей по способу средней арифметической простой величины, т.е. полученный результат оказывается заниженным, и по этому диаметру объёмы новых емкостей будут меньше объемов имеющихся емкостей, что не соответствует условию задания. Дело в том, что площади оснований цилиндрических емкостей соотносятся между собой не линейно, а как квадраты их радиусов. Поэтому рассчитывать средний диаметр новых емкостей целесообразно по средней квадратической простой величине:

Таким образом, диаметр оснований новых емкостей должен быть не 3,5, а 3,8 м.

Если же исходные данные представлены в виде дискретного или интервального ряда, то целесообразно применить способ средней квадратической взвешенной величины. Например, необходимо рассчитать средний диаметр сосновых брёвен по данным табл. 6.5.

Диаметр брёвен (варианта) представлен в виде интервального ряда, при этом число их (частота) по каждой группе кратно 10. Это означает, что при расчёте среднего диаметра брёвен в штабеле можно воспользоваться вторым свойством средней величины и сократить частоту каждой группы в 10 раз. Расчет среднего диаметра бревен в штабеле выполняем по формуле 6.7, (табл. 6.6).

С учётом применения второго свойства средних величин конечный расчёт среднего диаметра брёвен в штабеле принимает вид:

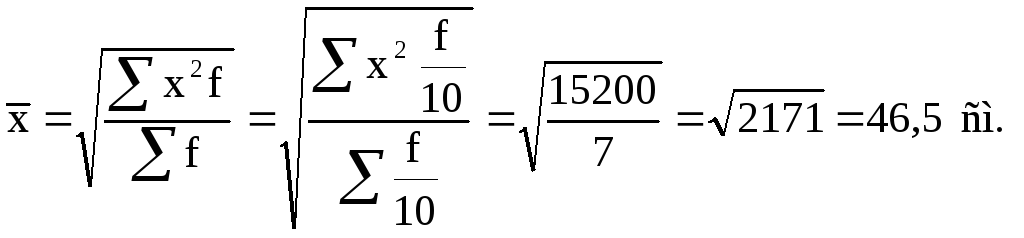
Т а б л и ц а 6.5. Число и размер брёвен в штабеле

Число брёвен	Диаметр, см
	в вершине	в комле
10	25	35
20	35	45
30	45	55
10	55	65

Т а б л и ц а 6.6. Порядок расчета среднего диаметра брёвен в штабеле

Число брёвен		Диаметр, см		Середина интервала, см	Квадраты диаметра	Взвешенные квадраты диаметра
фактически., шт	сокращенное	в вершине	в комле
f				x	х2	х2
10	1	25	35	30	900	900
20	2	35	45	40	1600	3200
30	3	45	55	50	2500	7500
10	1	55	65	60	3600	3600
Σ 70	7	-	-	-	-	15200

Таким образом, средневзвешенный диаметр сосновых брёвен в штабеле, рассчитанный по способу средней квадратической величины, составляет 46,5 см.

Главная сфера применения средней квадратической величины (в невзвешенной и взвешенной формах) – нахождение среднего квадратического отклонения.

6. Средняя геометрическая величина

Если в формулу 6.1 подставить значение К=0, то в результате получаем среднюю геометрическую величину, которая имеет простую (невзвешенную) и взвешенную формы.

Средняя геометрическая простая величина, рассчитываемая в ранжированном ряду, выражается следующим образом:

(6.8)

где – знак произведения; х – варианты;n – общее число вариант в ранжированном ряду.

Для дискретного или интервального ряда средняя геометрическая рассчитывается по взвешенной форме:

(6.9)

где f – частота дискретного или интервального ряда.

Средняя геометрическая величина применяется в тех случаях, когда варианты связаны между собой знаком произведения, т.е. главным образом при расчёте относительных показателей динамики: средних коэффициентов (темпов) роста, прироста и др.

Например, необходимо рассчитать, во сколько раз в среднем возросло производство сахарной свеклы в сельскохозяйственной организации за четырёхлетие, если известно, что цепные коэффициенты роста по годам составляли соответственно 1; 0,9; 1,3; 1,5 раза. При решении этой задачи рассуждаем так: цепные коэффициенты роста не автономны, как в вариационном ряду распределения, а взаимозависимы, т.е. связаны между собой знаком произведения. Следовательно, наиболее точный результат может быть получен при условии применения средней геометрической невзвешенной величины по формуле (6.8):

Таким образом, производство сахарной свеклы в приведенном четырехлетии за каждый год в среднем возрастало в 1,151 раза.

Если есть дискретный или интервальный ряд, то при расчёте средней целесообразно воспользоваться взвешенной формой средней геометрической величины. Допустим, необходимо рассчитать среднегодовой темп роста валового производства картофеля в районе за 20-ти летний период по данным табл. 6.7.

Т а б л и ц а 6.7. Динамика валового производства картофеля в районе

Темпы роста производства картофеля, %		Число лет в каждом периоде
Интервалы	Середина интервала
	х	f
90-100	95	3
100-110	105	6
110-120	115	6
120-130	125	5
Σ	-	20

Как видно, темпы роста производства картофеля представлены в виде интервального ряда, а они связаны между собой знаком не суммы, а произведения. Это означает, что для расчёта среднего темпа роста за весь 20-ти летний период целесообразно применить взвешенную форму средней геометрической величины (формула 6.9):

Таким образом, за двадцатилетний период производство картофеля развивалось со среднегодовым темпом роста 100,2 %.