32. Критерий g Кохрена.

Основан на сопоставлении сумм квадратов отклонений от средней арифметической, что сближает его с однофакторным дисперсионным анализом. Применяется для решения вопроса об однородности результатов нескольких серий экспериментов. Определяется сумма дисперсий всех серий экспериментов, после чего вычисляется отношение максимальной дисперсии к данной сумме:

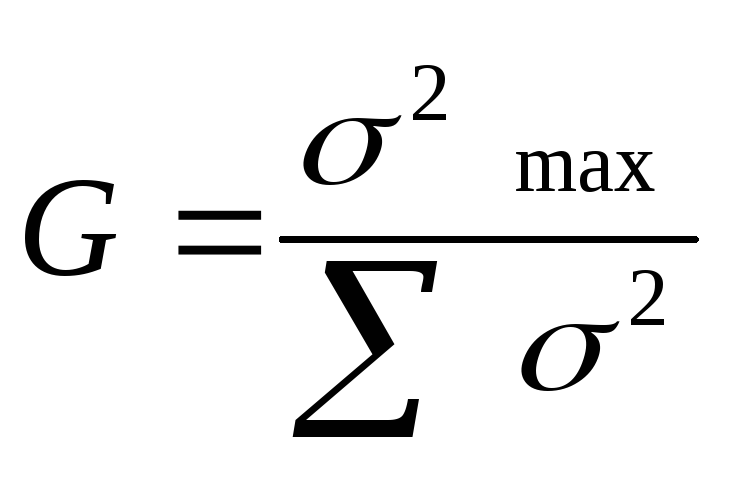Фактический материал считается однородным, если величина G не будет превышать табличное значение.

Например, в трех сериях экспериментах регистрировались значения биохимического показателя крови у 6 лабораторных животных

	Результаты измерений						Х сред	σ2
1 серия	3	5	4	5	5	4	4,3	0,7
2 серия	2	5	4	6	5	6	4,7	2,3
3 серия	4	4	3	2	1	5	3,2	2,2

Сумма дисперсий = 5,2 максимальная дисперсия – 2,3.

при р < 1 % и n = 6 G_ф (0,44)  Gт (0,70)

ВЫВОД: фактический материал однороден.

Таблицы нормального распределения

Ниже приводятся примеры использования таблиц нормального распределения для расчета наиболее вероятных частот и значений для заданных статистических параметров выборки.

1). Средняя масса тела морских свинок X =400г. Дисперсия σ²= 225. Объем выборки n = 320. Сколько животных при нормальном распределении с наибольшей вероятностью будут иметь массу тела более 420 г.?

Находим стандартное отклонение σ.

σ =√ σ² = √225 = 25.

Вычисляем нормированное отклонение для значения 420.

t = 420 – 400 / 25 = 1,33.

Количество вариант (в%), превышающих значение t = 1,33 находим

по таблице 5 «Доли площади под нормальной кривой, отсекаемые t справа отсредней». Эта величина составляет 9,18% (100% - 90,8%).

Составляем пропорцию 400 : 100 = Х : 9,18

Отсюда Х = 400 х 9,18 / 100 = 36,7 ≈ 37 (морских свинок).

2). Средняя длина побега растений данного вида

X = 24 см. Дисперсия σ²=25. Объем выборки n = 810. Сколько побегов с наибольшей вероятностью не будут превышать величину 19,5 см., если выборка подчиняется закону нормального распределения?

Находим стандартное отклонение σ.

σ =√ σ² = √25 = 5.

Вычисляем нормированное отклонение для значения 19,5.

t = 19,5 – 24 / 5 =-4,5 / 5 = -0,9

Количество вариант (в %) , не превышающих значение t = - 0,9 находим по

таблице 4 «Доли площади под нормальной кривой, отсекаемые t слева от средней». Эта величина составляет 18,41%.

Составляем пропорцию 810 : 100 = Х : 18,41

Отсюда Х = 810 х 18,41 / 100 =149,12 ≈ 149 (побегов).

3). Среднее количество лепестков у цветков георгина X = 120. Дисперсия σ²=400. Объем выборки n = 300. Сколько цветков с наибольшей вероятностью будут иметь количество лепестков в диапазоне от 75 до 140, если выборка подчиняется закону нормального распределения?

Находим стандартное отклонение σ.

σ =√ σ² = √400 = 20.

Вычисляем нормированное отклонение для значения 75:

t₁ = 75 – 120 / 20 =-45 / 20 = - 2,25

Вычисляем нормированное отклонение для значения 140:

t₂ = 140 – 120 / 20 =-20 / 20 = 1,0

Для определения заданного диапазона используем обе названные выше таблицы.

Процентное количество вариант, находящихся левее значения t₂ = 1,0 определяем по таблице 5 «Доли площади под нормальной кривой, отсекаемые t справа от средней». Эта величина составляет 84,13 %.

Количество вариант, не превышающих значение t₁ = - 2,25 находим по

таблице 4 «Доли площади под нормальной кривой, отсекаемые t слева от средней». Эта величина составляет 1,22 %. Вычисляем процентное количество вариант, располагающихся в заданном диапазоне: 84,13 % - 1,22 % = 82,91 %.

Находим количество цветков с количеством лепестков от 75 до 140.

300 : 100 = Х : 82,91

Отсюда Х = 300 х 82,91 / 100 =248,7 ≈ 249 (цветков).

4). Среднее количество митохондрий в клетках соединительной ткани X = 28. Дисперсия σ²=16. Объем выборки n = 200. В каком количестве клеток с наибольшей вероятностью будет найдено а) 28; б) 25; в) 20; г) 15 митохондрий в случае нормального распределения вариант?

Находим стандартное отклонение σ.

σ =√ σ² = √16 = 4.

Определяем множитель, необходимый для вычисления теоретических частот нормального распределения n / σ.

n / σ = 200 / 4 = 50

Вычисляем нормированное отклонение для значения 28:

t_а = 28 - 28 / 4 = 0

По таблице 1 «Значение функции у = f(t)» находим ординату кривой нормального распределения, соответствующую t_а = 0. В долях единицы она составляет 0,3989.

Вычисляем теоретическую частоту встречаемости клеток, имеющих 28 митохондрий для выборки n = 200.

у_{а х (}n / σ) = 0,3989 х 50 = 19,9 ≈ 20 (клеток)

Остальные расчеты производятся по такому же алгоритму.

Вычисляем теоретическую частоту встречаемости клеток, имеющих 25 митохондрий для выборки n = 200.

t_б= 25 - 28 / 4 = - 3 / 4 = -0,75

у_б = 0,3011 f = 0,3011 х 50 = 15,1 ≈ 15 (клеток)

Вычисляем теоретическую частоту встречаемости клеток, имеющих 20 митохондрий для выборки n = 200.

t_в= 20 - 28 / 4 = - 2,0

у_в = 0,0540 f = 0,0540 х 50 = 2,7 ≈ 3 (клетки)

Вычисляем теоретическую частоту встречаемости клеток, имеющих 15 митохондрий

t_г= 15 - 28 / 4 = - 3,25

у_г = 0,0020 f = 0,0020 х 50 = 0,1 (клетки)

При обычных уровнях значимости последняя величина может игнорироваться.

Z и φ – преобразование

Так как распределение выборочных коэффициентов корреляции отличается от нормального, при экстраполяции результатов корреляционного анализа на генеральную совокупность появляется ощутимая статистическая погрешность. Для более корректного представления результатов производится преобразование коэффициентов корреляции в числа Z по формуле:

. Производные числа Z распределяются в соответствии с нормальным законом и могут использоваться для проверки выборочных коэффициентов корреляции на достоверность, нахождения доверительного интервала коэффициента корреляции генеральной совокупности а также решения вопроса о достоверности разницы двух выборочных коэффициентов корреляции.

Схожая проблема появляется при анализе альтернативной вариации, когда доля объектов выборки, характеризующаяся наличием определенного признака (Р) выражается в долях единицы или в процентах. В этом случае квазинормальное распределение получают проценты в числа φ по формуле: φ = 2arcsin √ p