12. Критерий s Вальда - Вольфовица

Непараметрический критерий, называемый также тестом серий. Основан на анализе закономерностей последовательности распределения объектов двух несвязанных выборок. Может применяться при анализе количественной, ранговой и альтернативной вариации. В силу своего своеобразия имеет ограниченное применение, хотя в некоторых случаях может оказаться эффективнее других методов.

При количественной или ранговой вариации строится общий ранжированный ряд. Совокупность располагающихся рядом вариант одной выборки образует серию.

В случае альтернативной вариации важное значение имеет последовательность противоположных событий. Одноименные события (рождение нескольких детей одного пола, несколько падений монеты одной и той же стороной), также определяется как серия. Считается статистически маловероятным появление как малого количества больших серий, так и большого числа малых серий. Поэтому в таблицах критических значений данного критерия для каждого сочетания n приводится два числа (таблица 13). Нулевая гипотеза не может быть отвергнута до тех пор, пока S_ф (общее количество серий) находится в диапазоне, определяемом критическими величинами таблицы.

Например, последовательность падения монет орлом (О) и решкой (Р) образуют ряд О О Р Р Р Р О Р Р О О О Р Р О Р, состоящий из 8 серий образуют 7 «О» и 9 «Р». На пересечении строки 7 и колонки 9 в таблице находим 2 числа 4 и 14. Они представляют границы зоны незначимости. Количество серий – 8 попадает в эту зону, что свидетельствует о случайном характере наблюдаемых различий.

13. Критерий t Сиджела-Тьюки

Обладает большой статистической мощностью. Используется при сопоставлении результатов измерений проведенных на двух несвязанных выборках, объем которых может различаться.

Все варианты располагаются в виде общего ранжированного ряда с указанием принадлежности результата каждого измерения к первой или второй выборке. В отличие от рассмотренных выше критериев, где присвоение рангов проводилось последовательно слева направо, использование данного критерия предполагает совершенно иную процедуру. Членам общего ранжированного ряда присваивают ранги по схеме: первый ранг получает начальная варианта общего ряда, второй и третий - последняя и предпоследняя соответственно. Следующие два ранга (4 и 5) присваивают второй и третьей вариантам начала ряда и снова переходят в его конец. Таким образом движение осуществляется с обоих концов ряда попеременно к центру. Это продолжается пока всем вариантам не будут присвоены порядковые номера. Дальнейшие вычисления производятся по приводимой ниже формуле, где

ΣRi - сумма рангов меньшей выборки n₁, а n₂ - объем большей выборки. Особенностью данного метода является то, что хотя он и предполагает присвоение рангов, как для непараметрических критериев, для статистического заключения используется таблица Стюдента, основанная на параметрах нормального распределения.

Нулевая гипотеза отклоняется если фактическое значение окажется больше табличного

при df = n₁ + n₂ - 2.

Пусть n₁ = 6 (подеркнутые цифры) и n₂ = 8 (цифры не подчеркнуты).

Ниже приводится пример ранжирования:

Xi: 12 13 14 15 16 17 19 20 24 25 31 34 37 39

R: 1 4 5 8 9 12 13 14 11 10 7 6 3 2

ΣRi - сумма рангов меньшей выборки n₁ = 42, N = 6 + 8 = 14.

Подставляем значения в формулу: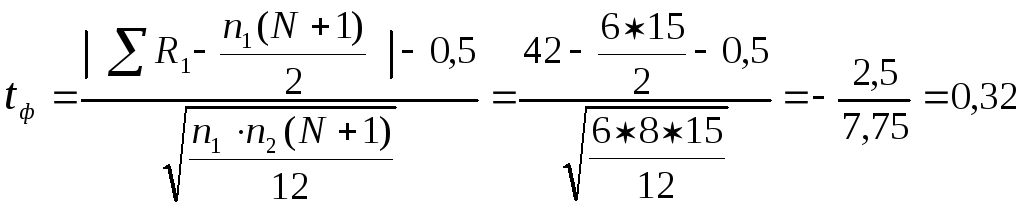

При р < 5 % и df = n₁ + n₂ = 12 + 14 – 2 = 24 t_ф (0,32)  t_т (2,06)

ВЫВОД: нулевая гипотеза сохраняется.