чивается. Поэтому в силу одногорбости биномиального закона распределения все вероятности Pn (k) оказываются очень малыми. В частности, при k значи-

тельно отличающихся от математического ожидания np, величины вероятностей Pn (k) будут настолько малы, что ими можно пренебречь, т.е. считать их равными

нулю. Следовательно, необходимо оценить вероятности Pn (k) только для значе-

ний k, достаточно близких к np, т.е. к математическому ожиданию биномиального распределения.

Один из полезных приемов состоит в рассмотрении отношения Pn (k +1) вме-

Pn (k)

сто самих Pn (k) . Он уже использовался раньше. Другое средство − переход к вычислению ln Pn (k) . Тогда остаются только логарифмы факториалов от k, n, n − k и

степеней pk , qn−k . В результате Pn (k) заменяются более простыми и удобными

функциями, которые определяются математическим ожиданием и дисперсией случайной величины.

Таким образом, когда число испытаний n увеличивается и становится достаточно большим, вычисление вероятностей биномиального распределения Pn (k) упрощается. После перехода к пределу n → ∞ для определения функции

распределения остается найти только M ( X ) и D( X ) . Рассмотрим один из предельных случаев при n → ∞.

Тема 22. Распределение Пуассона

В первом случае математическое ожидание числа успехов pn все время по-

стоянно, т.е. np = λ . Тогда p = λn и p → 0 , q =1 − p →1, когда n → ∞.

Условие p → 0 означает, что успехи должны появляться достаточно редко.

Поэтому говорят, что в рассматриваемом случае биномиальное распределение описывает редкие события, и это, конечно, относится и к распределению, получающемуся после предельного перехода.

В силу (4.10) и (4.11), учитывая, что k << n, р → 0, q → 1 , получаем:

59

Перемножив последовательно первые два, три и больше полученных равенств, находим:

Общий множитель P (0) в этих равенствах легко найти. Действительно, получаем:

где сумма в скобках равна eλ , а сумма вероятностей в левой части всегда равна единице. Следовательно:

Полученное распределение называется распределением Пуассона.

Таким образом, если математическое ожидание числа успехов остается равным λ , когда число испытаний n становится достаточно большим, распределение Пуассона определяет вероятности получения числа успехов. Конечно, эти вероятности возрастают, если k < λ , и убывают, когда k > λ.

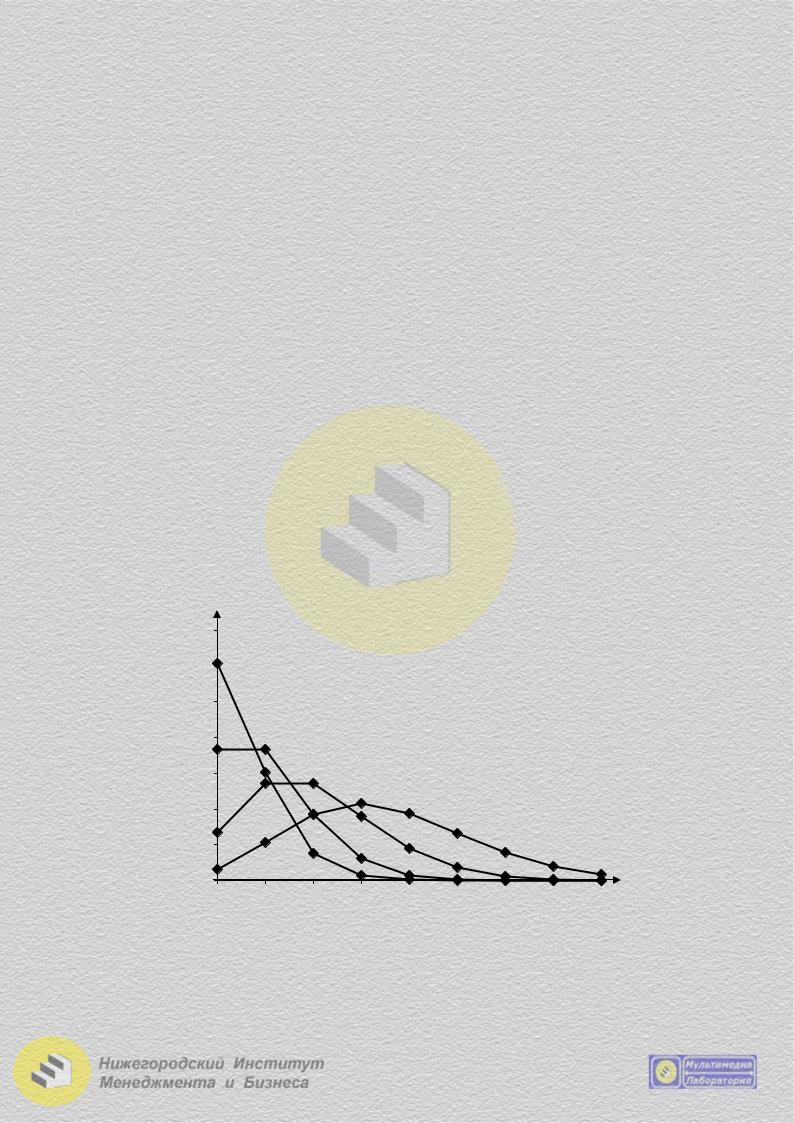
На рис. 2.7 показаны многоугольники распределения случайной величины X , распределенной по закону Пуассона, соответствующие различным значениям параметра λ .

Рис. 2.7. Многоугольники распределения для случайной величины, распределенной по закону Пуассона, соответствующие

различным значениям параметра λ

Для вычисления вероятностей в законе распределения Пуассона составлены таблицы, которыми легко пользоваться при различных k и λ . В тех случаях, ко-

60

гда np = λ <10 , распределение Пуассона дает результаты, очень близкие к точ-

ным. Поэтому в таблицах распределения Пуассона предполагается, что λ <10 . Приведем типичные примеры применения распределения Пуассона для

отыскания вероятностей.

Пример 23. Приобретенная фирмой партия товара содержит 1000 электролампочек. Вероятность повреждения каждой лампочки при доставке – 0.002. Найти вероятность того, что при доставке будет повреждено 5 лампочек.

Решение. В этой задаче число поврежденных при доставке лампочек есть случайная величина. Она подчиняется биномиальному распределению с n =1000 и p = 0.002 . Поэтому вероятность того, что поврежденными окажутся 5 лампо-

таточно громоздко для вычисления. Проще применить распределение Пуассона, так как здесь наивероятнейшее значение числа поврежденных при доставке лампочек равно np =1000 0.002 = 2 = λ <10 . Тогда для искомой вероятности полу-

лучаем также закон распределения числа поврежденных лампочек при заданных условиях ( λ = 2) (табл. 2.18):

В этой таблице сумма вероятностей меньше единицы на 0.0032. Причина заключается в том, что для конкретного закона распределения опущены вероятности того, что X > 8 , так как все они малы. Из приведенного закона распределения следует, что число поврежденных при доставке лампочек – не более 6 с вероятностью больше, чем 0.98.

Пример 24. Вероятность изготовления бракованного изделия равна 0.0003. Найти вероятность того, что в партии из 10000 изделий окажется: а) 5 бракованных изделий; б) не более 5 бракованных изделий.

Решение. Здесь λ =10000 0.0003 = 3 и, следовательно, используя распреде-

ление Пуассона, получаем: P10000 (5) = 35 e−3 ≈ 0.101 для задания (а) и ≈ 0,91 –

5!

для (б). Так же, как и в предыдущем примере, по таблице распределения Пуассона здесь легко найти закон распределения и на его основе понять, какие выгоды можно получить, если добиться повышения качества изготовления изделия, т.е. уменьшения вероятности брака, и, наоборот, оценить возможные потери из-за увеличения вероятности брака.

61

Пример 25. Предприятие отправляет на базу 2000 изделий. Вероятность повреждения изделия в пути – 0.001. Составить закон распределения числа поврежденных изделий, если их число равно значениям m = 0, 1, 2, 3, 4, 5, 6, 7.

Решение. Условие задачи соответствует схеме Бернулли с исходными данными: n = 2000 , P(A)= p =0,001 = const , причем p << 0.1, событие A – повреж-

дение изделия в пути, np = 2000 0.001 = 2, т.е. λ =np =2 <10, m =0, 1, 2, 3, 4, 5, 6, 7 . Вероятности pi = P(X = m) находятся по таблице функции Пуассона с парамет-

рами λ = 2 и соответствующими значениями m , а закон распределения в табличном виде примет вид (табл. 2.19):

Заметим, что в рассмотренных примерах задача сводилась к использованию распределения Пуассона, когда λ = np <10 , несмотря на то, что речь шла о боль-

ших партиях доставки и изготовления товаров. По этой причине часто говорят, что распределение Пуассона хорошо описывает вероятности редких событий, т.е. случайные величины, которые описывают маловероятные (редкие) события.

Подчеркнем, что конкретные результаты, которые можно получать с помощью распределения Пуассона так же, как это сделано в рассмотренных примерах, дают полезные практические рекомендации для установления нормативных потерь и ограничений при заключении договоров и принятии решений. То же справедливо и для деятельности страховых компаний.

Задачи для самостоятельного решения

Задача 20. Астроном в благоприятную ночь наблюдает метеорный поток на определенном участке неба, регистрируя количество пролетевших метеоритов за каждые 15 минут. Полагая, что поток метеоритов – пуассоновский (подчиняется закону редких событий), и что в среднем можно наблюдать λ = 3 метеорита, составить закон распределения числа наблюдаемых за 15 минут метеоритов, если их число равно значениям m = 0, 1, 2, 3, 4, 5, 6, 7.

Задача 21. Владельцы кредитных карточек ценят их и теряют весьма редко. Пусть вероятность потерять в течение недели кредитную карточку для произвольного владельца равна 0.001. Всего банк выдал карточки 2000 клиентам. Найти вероятность того, что в предстоящую неделю будет потеряна: а) ровно одна кредитная карточка; б) хотя бы одна кредитная карточка. Сколько в среднем теряется карточек за неделю? Составить закон распределения числа потерянных карточек за неделю, если их число равно значениям m = 0, 1, 2, 3, 4, 5.

62