3.1.5. Кореляційний момент випадкових величин

Означення 1. Кореляційним моментом (кореляцією, коваріацією) K(X,Y) випадкових величин X та Y називається число

K(X,Y)=M. (10)

Ця величина має розмірність, що дорівнює добутку розмірностей випадкових величин X та Y. Скориставшись властивостями математичного сподівання, можна привести формулу (10) до вигляду

K(X,Y)=M(X·Y)–MX·MY. (11)

Випадкові величини називаються корельованими при K(X,Y)0 і некорельованими при K(X,Y)=0. Якщо випадкові величини незалежні, то із (9) виходить, що K(X,Y)=0 – із незалежності випадкових величин випливає їх некорельованість. Якщо K(X,Y)0, то випадкові величини є залежними ‑ із корельованості випадкових величин випливає їх залежність. Однак, із K(X,Y)=0 не випливає незалежність випадкових величин – із некорельованості випадкових величин не випливає їх незалежність. Приклад таких величин приведено в зауваженні до теореми 3 пункту 3.1.4. Отже,

Незалежність некорельованість

Корельованість  залежність

П

X Y	1	2
2	0.3	0.5
3	0.1	0.1

риклад 1. Знайти кореляційний момент координат випадкового вектора, заданого таблицею:

Розв’язок. За формулами (5) та (7) знаходимо

Тоді за формулою (11) одержимо

K(X,Y)=3.5–2.2·1.6= – 0.02.

Приклад 2. Випадковий вектор рівномірно розподілений в областіD{(x;y): 0<y<x², 0<x<1}(мал.3.2). Знайтикоре­ляційниймомент його координат.

Розв’язок. Площа областіDдорівнює . Отже, , якщо(x; y)D. Тому на підставі формул (5), (7), (11) маємо:

3.2. Дисперсія випадкової величини

3.2.1. Дисперсія випадкової величини та її властивості

Після того, як математичне сподівання випадкової величини знайдено, виникає питання, наскільки сильно значення випадкової величини від­хиляється від математичного сподівання. Характеристикою ступеня розсіювання випадкової величини навколо математичного сподівання є математичне сподівання квадрата флуктуації випадкової величини (математичне сподівання флуктуації не придатне, тому що воно завжди дорівнює нулю). Інколи в якості характеристики розсіювання випадкової величини використовують математичне сподівання абсолютної величини її флуктуації.

Означення 1. Дисперсією випадкової величини називається невід’ємне число

DX=M()². (1)

Розмірність дисперсії дорівнює квадрату розмірності випадкової величини. Тому вводять також величину , що називаєтьсясереднім квадратичним(стандартним) відхиленням, вимірність якої співпадає з вимірністю випадкової величини.

Чим менше _X(DX), тим тісніше групуються значення випадкової величини навколо її математичного сподівання.

Дисперсія допускає важливе математичне тлумачення. Нехай i –сила струму, що проходить через резистор з опором 1 Ом. Тоді потужність, яка виділяється флуктуаційною складовою струму дорівнює , а її середнє значенняM. Таким чином, дисперсія струму дорівнює середній потужності, яка виділяється флуктуаційною складовою струму на резисторі з одиничним опором.

При знаходженні дисперсії, як правило, використовують не формулу (1), а інший вираз, який одержується з правої частини цієї формули на підставі властивостей математичного сподівання:

Таким чином,

(2)

Якщо X=Y, то кореляційний момент дорівнює дисперсіїK(X,X)=DX. Запишемо формулу (2) у розгорнутому вигляді

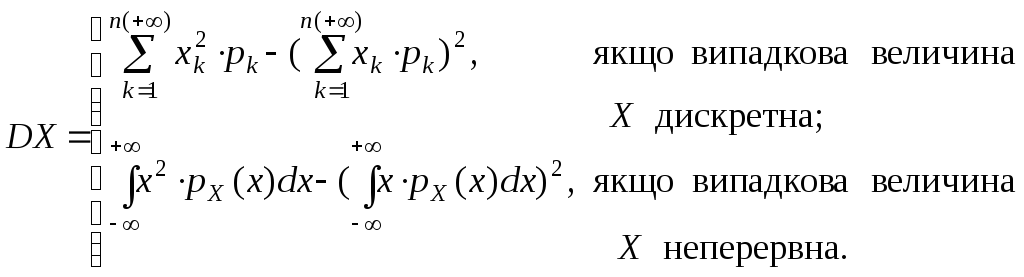(2´)

Із формули (1) випливає, при сталих kіl, важлива властивість дисперсії

D(kX+l)=k²DX. (3)

Дійсно, з урахуванням властивостей математичного сподівання, одержимо

D(kX+l)==k ²·DX.

Зокрема, дисперсія константи (сталої величини) дорівнює нулю.

Приклад 1. При умові прикладу 1 пункту 3.1.2 знайти дисперсію випадкової величиниX.

Р

X2	0	1
P	1–p	p

озв’язок. Із прикладу 1 пункту 3.1.2 маємоMX=p. Оскільки  тоMX ²=0·(1–p)+1·p=p і на підставі формули (2) одержимо

DX=p– p²=p·(1– p).

Приклад 2. Знайти дисперсію випадкової величиниX, розподіленої за законом Пуассона (розділ 2.1, формула (5)).

Розв’язок.

(тут двічі використане розкладання експоненти у ряд ). Було показано (приклад 2 пункту 3.1.2), щоMX=. Отже,DX=²+–²=– параметр закону Пуассона співпадає як з математичним сподіванням, так і з дисперсією.

Приклад 3. Знайти дисперсію випадкової величиниX, розподіленої:1) рівномірно в проміжку [c; d]; 2) за показниковим законом з параметром ; 3) зазаконом Гауса з параметрамиa і²; 4) за законом Релея з параметром ².

Розв’язок. При розв’язанні будуть використані формули (2) та (1) і також результати пункту 3.1.2 (приклади 3,4, наслідки теореми 1).

¹⁾ ;

²⁾

³⁾

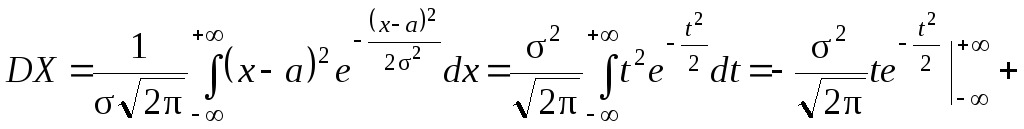
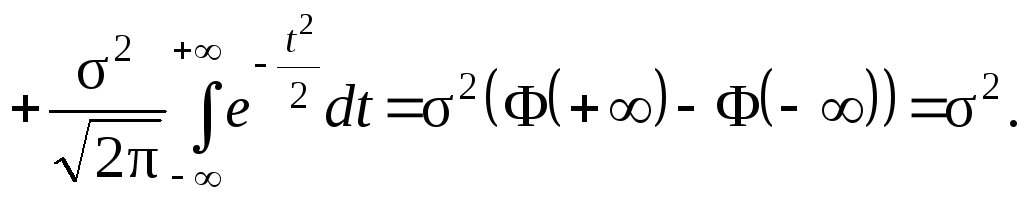
Таким чином, параметрами закону Гауса N(a;²) є математичне сподіванняa і дисперсія²;

4)

Отже, .

Випадкова величина Xназиваєтьсянормованою, якщоMX=0,DX=1. Прикладом нормованої випадкової величини є випадкова величина . Дійсно,

Приклад 4. Знайти математичне сподівання і дисперсію випадкової величини_n²(²‑розподілом зnстепенями свободи).

Розв’язок._n²=X₁²+X₂²+...+X_n², деX_i-незалежні та розподілені за законом ГаусаN(0;1). Використовуючи властивості математичного сподівання та дисперсії, одержимо:

M_n²=M(X₁²)+...+M(X_n²)=nM(X_i²), D_n²=D(X₁²)+...+D(X_n²)=nD(X_i²).

Оскільки DX_i=M(X_i²)–(MX_i)², тоM(X_i²)=DX_i+(MX_i)²=1,

D(X_i²)=M(X_i⁴)–(M(X_i²))²=M(X_i⁴)–1. ОтжеM_n²=n. Залишилось знайти величину

Тому =3–1=2 і остаточноD_n²=2n.

Зауваження.Для знаходження математичного сподівання і дисперсії нелінійної функціїf(X) часто користуються наближеними формулами:

Mf(X)  f(MX),

Df(X)  | f ´(MX)|² ·DX.

Ці формули тим точніші, чим менше f(X) функція відрізняється від лінійної. Для лінійної функціїf(X)=kX+l наведені формули є точними.