2.1.4. Перетворення розподілів

Нехай розподіл випадкової величини X є відомим. Потрібно знайти розподіл випадкової величиниY, яка пов’язана з функціональною залежністю Y=g(X) (Y приймає значення g(x), коли X приймає значення x).

1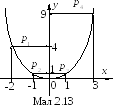) Випадкова величина X є дискретною. Тоді знаходять сукупність значень випадкової величиниYі ймовірності, з якими ці значення приймаються. У тому випадку, коли серед значеньg(x_k) немає однакових, маємоP{Y=g(x_k)}=P{X=x_k}=p_k. Якщо серед значеньg(x_k) є однакові, потрібно додавати відповідні ймовірності.

П

X	-2	-1	1	3
p	0.2	0.1	0.4	0.3

риклад 1. Випадкова величина X задана таблицею розподілу:

Знайти таблицю розподілу випадкової величини Y=X².

Р

Y	1	4	9
p	0.5	0.2	0.3

озв‘язок. Метод побудови таблиці розподілу випадкової величини зрозумілий з мал.2.13: вона має вигляд

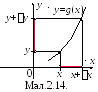2) Випадкова величина X є неперервною. У тому випадку, коли функціяg(x) має оберненуh(y), справедливе співвідношення

, (11)

яке виходить з того, що події {X[x;xx)} та {Y[y;yy)} є еквівалентними (мал.2.14).

Зауваження.Якщо функція не є монотонною, то формулу (11) слід використати на кожному проміжку монотонності а потім об’єднати одержані результати.

Приклад 2. Випадкова величинаXN(a;²). Знайти щільність ймовірності випадкової величини: 1)Y=AX+B; 2)Y=e^X.

Розв’язок. 1) Оскільки y=Ax+B, то і . Тому на підставі (11), одержимо

.

Таким чином, YN(aA+B; ²A²).

2) Оскільки оберненою по відношенню до функції e^x ( g(x)) є функція ln y ( h(y) ), то і на підставі формули (11) одержимо

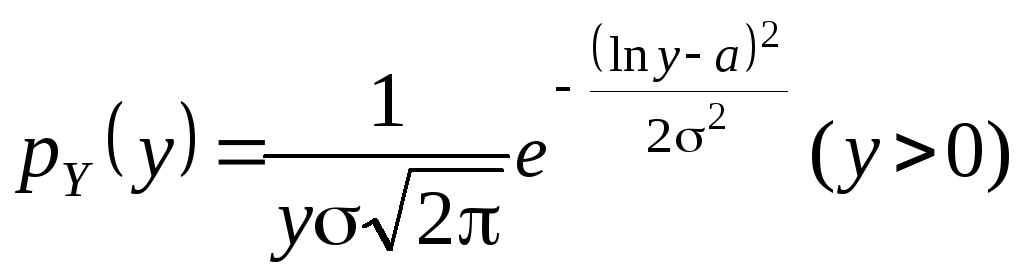. (12)

Розподіл (12) називається логнормальним. Він використовується при опису амплітуди, потужності та обвідної радіосигналу. Графік логнормального розподілу приведено на мал.2.15.

Приклад 3. Випадкова величинаXN(a;²). Знайти щільність ймовірності випадкової величиниY=X².

Розв’язок. Функція y=x² має дві обернені h₁(y) =,  h₂(y) = –. Тоді, за формулою (11) з урахуванням зауваження знаходимо

.

Графік цього розподілу при=1 приведено на мал.2.16.

2.2. Випадкові вектори

2.2.1. Функція розподілу випадкового вектора

Якщо кожний наслідок випробування задається упорядкованою сукупні­стю nвипадкових величин, то прийнято говорити проn-вимірнийвипадковий вектор. Виявляється, що для повного опису випадкового вектора потрібно мати не тільки інформацію про властивості його координат а і про їх взаємодію.

Наведемо приклади випадкових векторів: 1) точка попадання у плоску мішень характеризується випадковим вектором , деX таY координати точки попадання в системі координат, розміщеній в площині мішені; 2) стан будь-якого пристрою (від вольтметра до ЕОМ) характеризується сукупністю випадкових величин.

У подальшому найчастіше мова йтиме про двовимірний випадковий вектор .

Функцією розподілу двовимірного випадкового вектора називається задана у площиніxOyфункція така, що

.

2.2.2. Дискретний випадковий вектор

Y X	y1	y2	...	ym
x1	p11	p12	...	p1m
x2	p21	p22	...	p2m
...	...	...	...	...
xn	pn1	pn2	...	pnm

Якщо обидві координати вектора є дискретними випадковими величинами, то вектор називаютьдискретним випадковим вектором. Дискретний випадковий вектор задається набором значень(x_k; y_j)та ймовірностямиp_kj=P{X=x_k,Y=y_j},з якими ці значення приймаються. Дискретний випадковий вектор, як правило, задають таблицею розподілу.

Ясно, що сума всіх ймовірностей p_kjдорівнює одиниці.

У таблиці розподілу випадкового вектора міститься вся інформація про нього. Зокрема, ця таблиця дозволяє знайти розподіл координат вектора.

Оскільки подія {X=x_k} складається з суми попарно несумісних подій {X=x_k,Y=y₁}, {X=x_k,Y=y₂},..., {X=x_k,Y=y_m}, то щоб одержати розподіл ймовірностейp_kвипадкової величиниXпотрібно просумувати ймовірностіp_kj,які стоять уk-мурядку таблиці:

p_k = P{X=x_k} = p_k1+ p_k2+...+p_km . (1)

При сумуванні ймовірностей p_kjпо стовпцях знаходимо розподіл ймовірностей випадкової величиниY.

Y X	-2	-1	2
0	0.15	0.05	0.25
1	0.35	0.2	0

Приклад 1. Знайти розподіл координат випадкового вектора , заданого таблицею розподілу:

Розв’язок. На підставі формули (1) одержуємо розподіли координат X таY:

X	0	1		Y	-2	-1	2
P	0.45	0.55		P	0.5	0.25	0.25

Виникає запитання: чи завжди можливо за розподілом координат зна­йти розподіл вектора? Виявляється, що відповідь на це питання негативна.

Введемо подібно до умовної ймовірності поняття умовного розподілу

. (2)

Випадкові величини X таYназиваютьсянезалежнимитоді, коли при всіх значенняхkтаjсправедливі співвідношення

.

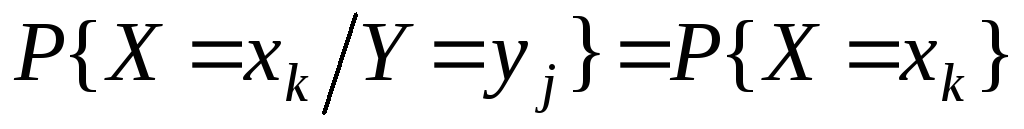Випадкові величини X таYнезалежні тоді і тільки тоді, коли при всіх значенняхkтаjвиконується рівність

.

Іншими словами, двовимірний розподіл вектора відновлюється по одновимірних розподілах його координат лише у тому випадку, коли координати вектора є незалежними випадковими величинами.

Приклад 2. В умовах прикладу 1 знайти умовні розподіли та з’ясувати питання про те, чи є випадкові величиниX таYзалежними.

Розв’язок. На підставі формули (2) знайдемо умовний розподіл X при Y=2:

.

Аналогічно одержуємо умовний розподіл при Y= –1 таY=2:

,

.

Випадкові величини X таYє залежними, наприклад, тому що

.