12.2 Выбор элементов памяти автомата

Замена таблиц переходов ЦА на структурную таблицу переходов приводит к тому, что функция переходов ЦА становится векторной. В соответствии со структурной таблицей переходов ЦА его векторная функциякаждой паре двоичных векторовставит в соответствие определенный двоичный вектор, что определяется соотношением. Из этого следует. Что структурный автомат должен запоминать двоичный вектор каждого очередного состояния ЦА, для чего служат элементы памяти.

При каноническом методе структурного синтеза автоматов в качестве элементов памяти используются элементарные автоматы Мура с двумя состояниями, обладающие полной системой переходов и выходов.

Полнота системы переходов-выходов для любой пары состояний ЦА существует входной сигнал, переводящий ЦА из одного состояния в другое.

Полнота системы выходов – различным состояниям автомата соответствуют различные выходные сигналы; обычно нулевому состоянию элементарного автомата соответствует нулевой выходной сигнал, а единичному состоянию - единичный выходной сигнал.

Число элементов памяти структурного автомата равно числу компонент вектора его состояний.

В качестве элементов памяти структурного автомата обычно используются D-, T -,RS- иJK- триггеры, удовлетворяющие требованиям относительно полноты переходов и выходов. Каждый из приведенных триггеров является автоматом Мура. ВходыD, T,RSиJKназываются информационными. Таблицы переходов триггеров составляются только для информационных входов. Остальные входы являются вспомогательными (C,R,S). Каждый триггер имеет два выходаи.

12.3 Выбор структурно-полной системы элементов

Функционирование структурного автомата во времени предполагает управление переключением каждого элемента автомата памяти в соответствии со структурной таблицей переходов синтезируемого автомата. Последнее выполняется в соответствии помощью специальной комбинационной схемы, подключаемой к информационным входам элементарного автомата памяти и реализующей булевы функции, управляющие его переключением. Такие булевы функции называют функциями возбуждения элемента памяти, и, в общем случае, различных функций возбуждения столько, сколько различных информационных входов имеется у элементарных автоматов памяти в синтезируемом структурном автомате. Функция возбуждения любого элемента памяти является произвольной булевой функцией и для ее реализаций с помощью комбинационных схем необходимо использовать какую-нибудь функционально-полную систему логических элементов.

Т.о. для построения структурного автомата, необходимо кроме элементов памяти иметь КС, реализующую булеву функцию возбуждения элементов памяти автомата, а для выработки выходных сигналов структурного автомата – специальные КС формирования выходных сигналов автомата.

Если векторная функция переходов задает переход из одного вектора состояния структурного автомата в другой вектор состояния под воздействием двоичного вектора входного сигнала, то векторная функция возбуждения автомата задает двоичный вектор, который нужно подать на входы элементов памяти автомата, чтобы обеспечить требуемый переход. Это означает, что переменными, от которых зависит функция возбуждения, являются те же переменные, что и для векторной функции переходов автомата, т.е. выходы всех элементов памяти автомата и входы структурного автомата. Поэтому структурный автомат Мура и структурный автомат Мили могут быть представлены соответствующими структурными схемами.

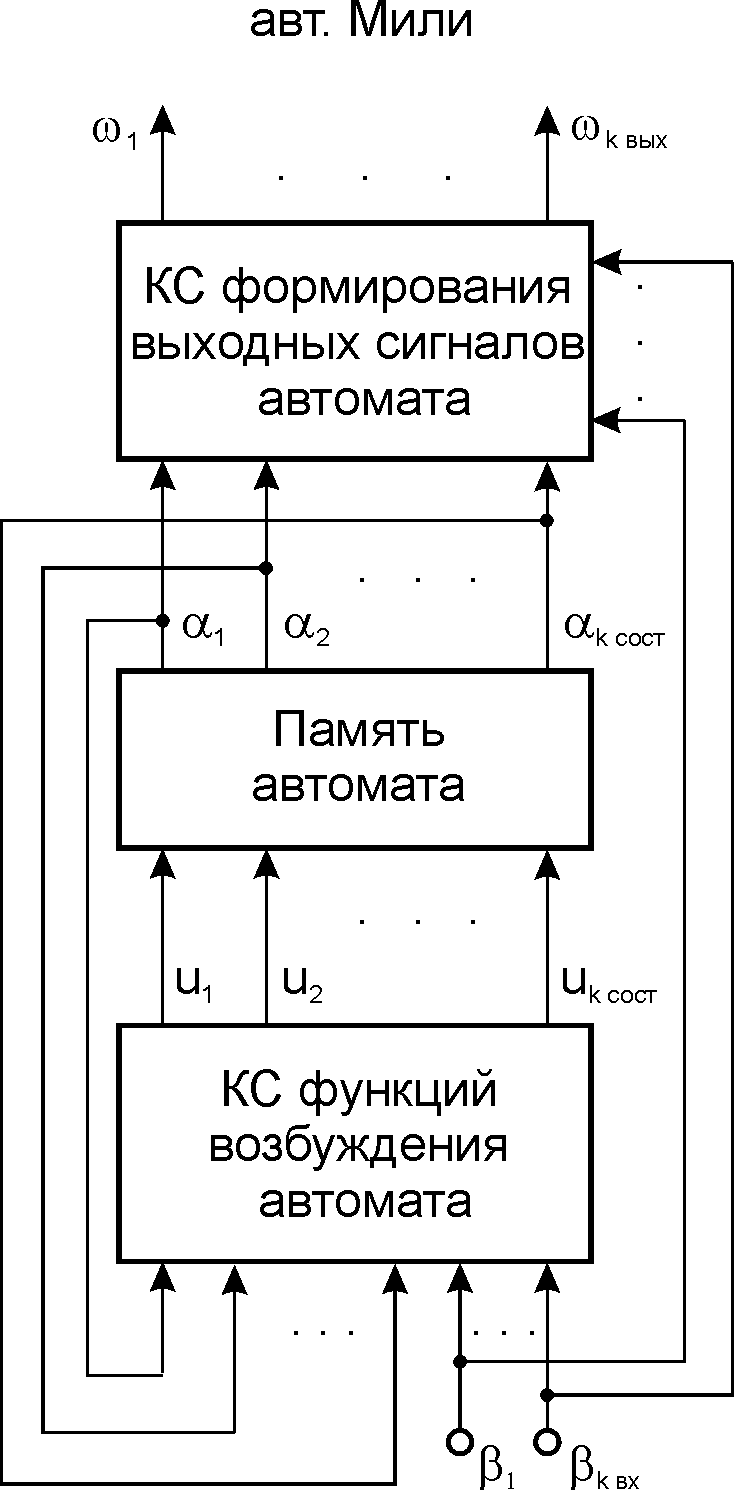
- выходы элементов памяти, где

- число элементов памяти;

- функции возбуждения элементов памяти;

- выходные каналы структурного автомата, где

- число выходных каналов.

Для автомата Мили, описанного табл. 1 получаем: необходимо два элемента памяти, т.к. векторы состояний – двухкомпонентные, необходимо два выходных и один входной каналы.