10.2. Постановка задачі лінійного програмування

Задача лінійного програмування (ЗЛП) формулюється так:

Знайти вектор , що мінімізує функцію

при таких обмеженнях:

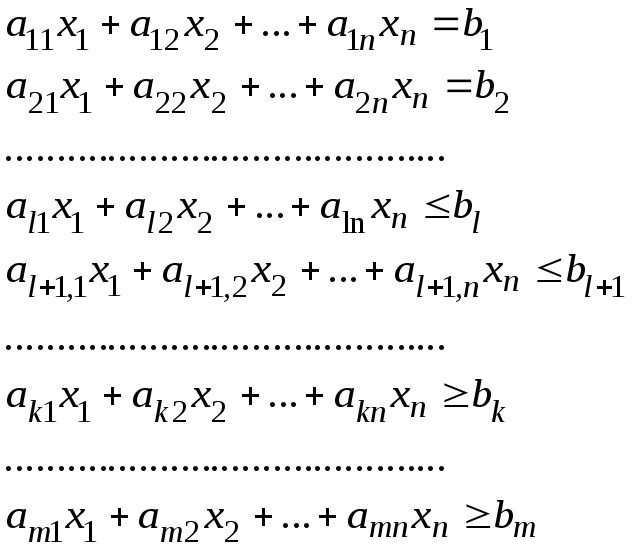(10.3)

Якщо всі обмеження позначаються знаком дорівнює, всі значення , а длязнаходять мінімум, то така модель називаєтьсяканонічною. Вона має вигляд:

при обмеженнях:

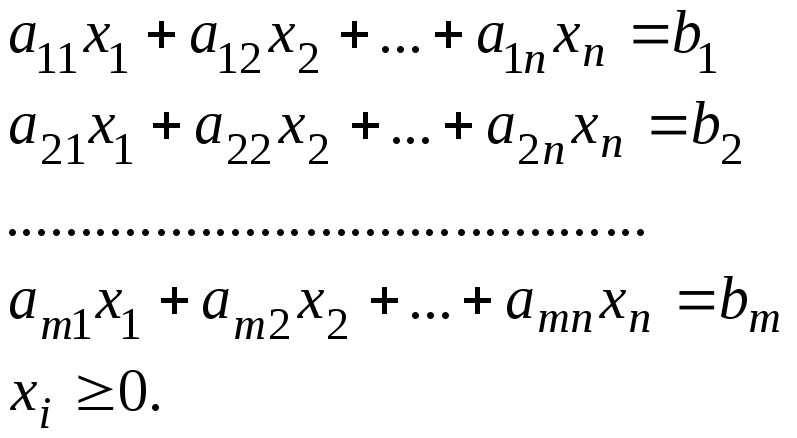(10.4)

Модель (10.3) можна привести до канонічної форми (10.4), скориставшись твердженнями:

1. 

2. ;

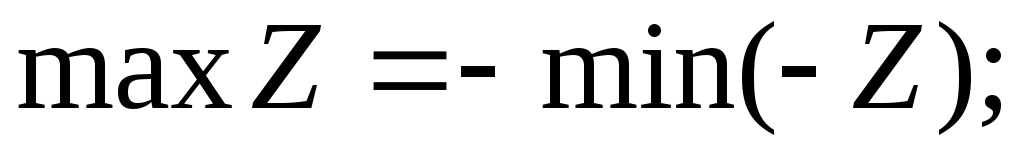
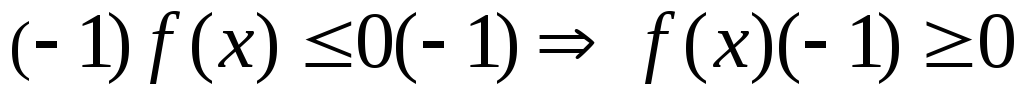3. розв’язок системи (10.3) з від’ємними значеннями 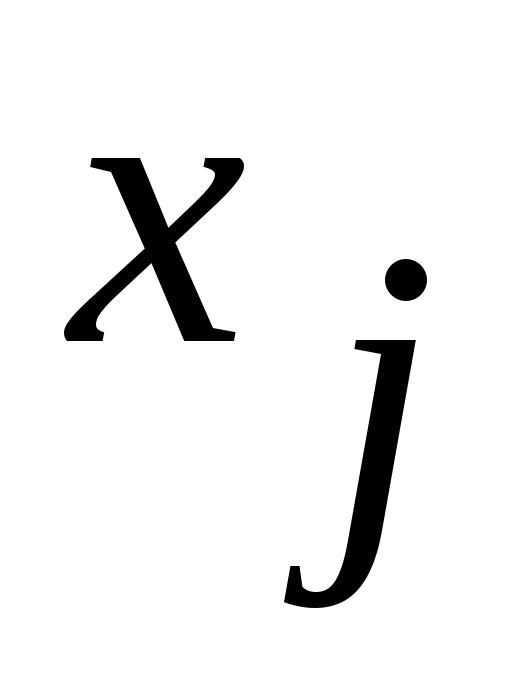можна звести до системи (10.4) з невід’ємними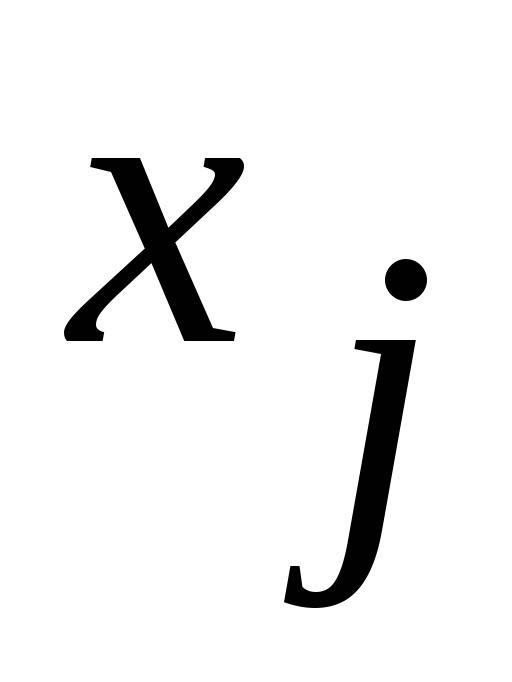, якщо від’ємні компоненти вектораХ замінити різницею двох додатніх:

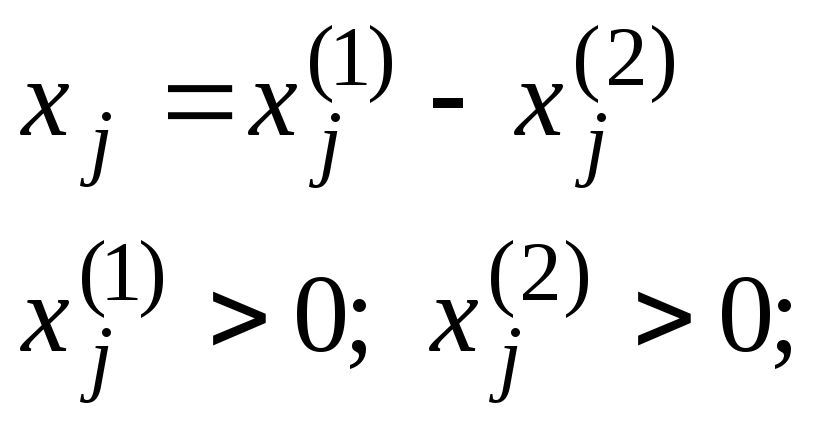
4. якщо 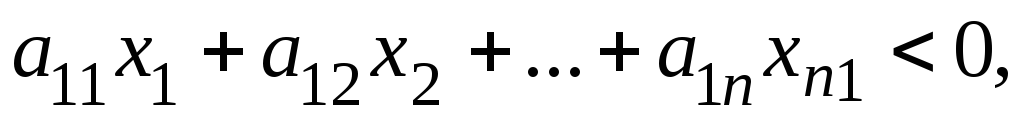то його можна замінити на рівність шляхом додавання в ліву частину невід’ємної змінної.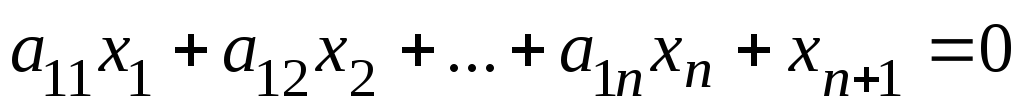

Канонічна модель в матричній формі має вигляд: при обмеженнях.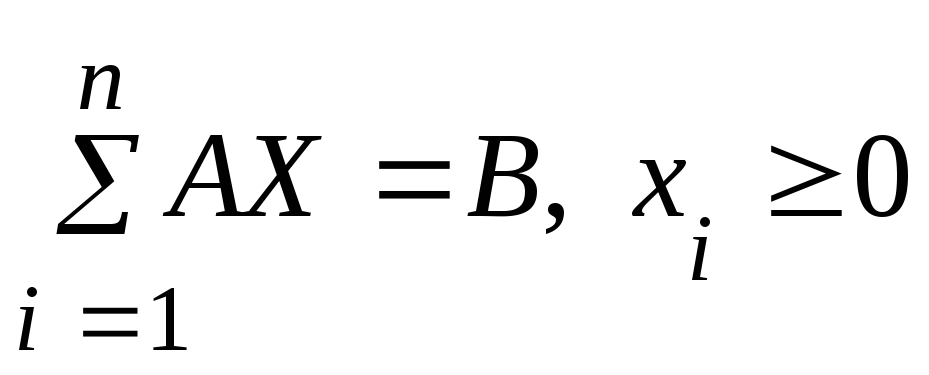

10.3. Геометрична інтерпретація злп

Якщо ЗЛП має лише два невідомих, її модель буде мати вигляд при обмеженнях:

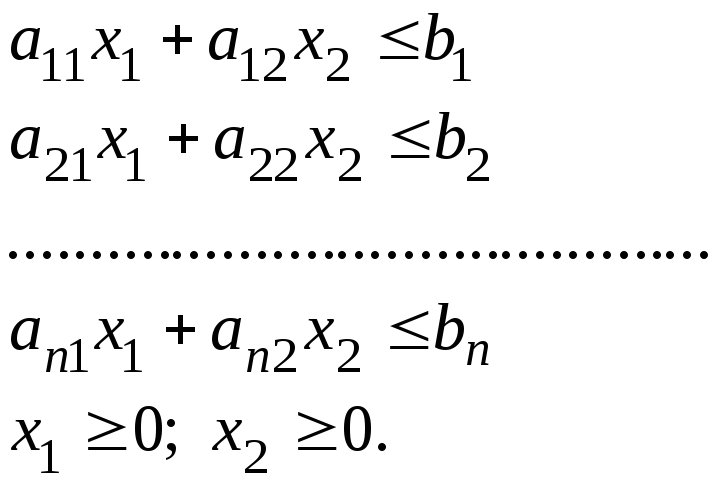
В цьому випадку кожне обмеження являє собою напівплощину, а їх сукупність створює зону розв’язку задачі. Дві останні нерівності вказують на те, що ця зона буде розміщена в першому квадранті координатної площини .

Цільова функція , являє собою пряму, що проходить через початок координат. Якщо цю пряму паралельно самій собі перемістити в останню точку зони розв’язку, то ця точка і буде оптимальною точкою розв’язку задач.

Продемонструємо цю теорію на практиці, розглянувши таку задачу.

Завод штучного полотна випускає два види продукції: шовкову нитку вартістю одиниць та корд вартістю. Випуск одного кілограму нитки дає в повітряний простір викидів: сірковуглецюкг, сірководнюкг, парів кислоткг. Аналогічні викиди від одного кілограму корду відповідно дорівнюють. Екологічною охороною заводу предписано за добу в повітря викинути не більше 200 кг, 400 кг сірководню та 300 кг кислот.

Зробити план випуску заводу таким, щоб прибуток від продажу продукції був найбільшим. Модель задачі має бути такою:

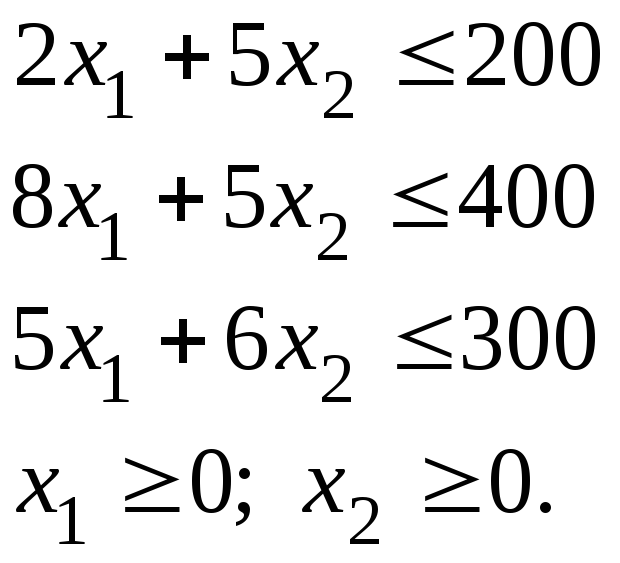
Накреслимо зону розв’язку в системі MathCad:

Графічний розв’язок злп

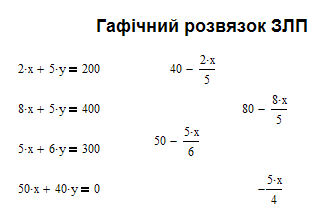
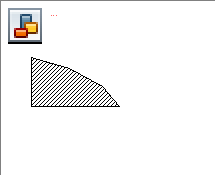
Як бачимо із графіка оптимальною точкою розв’язку задачі є перетин ліній та, тобто точка з координатамита. Цільова функція.

10.4. Симплекс-метод розв’язку злп

Задача прикладу розв’язувалась в двовимірному просторі. Область обмежень представляла собою п’ятикутник, в одному із кутів якого одержали точку максимума.

Якщо розв’язувати задачу з трьома невідомими, область розв’язку буде многогранником, в одному із кутів якого буде знаходитись оптимальне рішення. Якщо ж задача розв’язується в вимірному просторі, областю обмежень є гіпермногогранник –симплекс. Звідси походить назва методу.

Вибравши деякий базис перетворимо систему обмежень і цільову функцію в канонічну форму

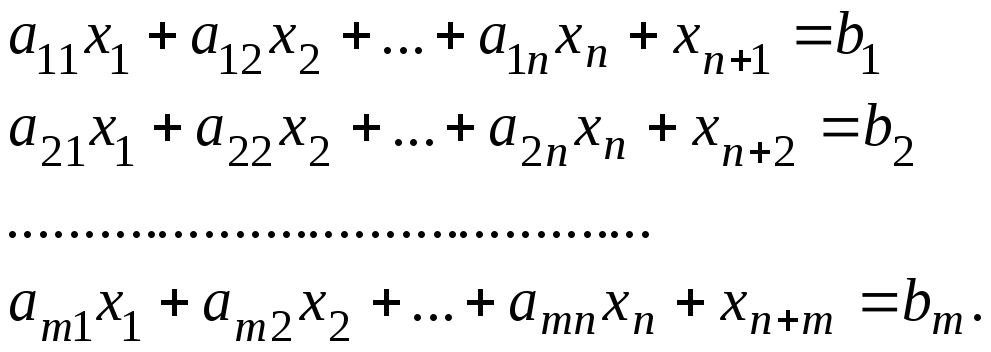
Із цієї системи створюємо таблицю:

Базис			…			…	b
			…	1	0	…	b1
			…	0	1	…	b2
…	…	…	…	…	…	…
			…	0	0	…	bm+n
Z			…	0	0	…	b0

Базис відповідає кожному куту симплекса. Перша таблиця відповідає початку координат. Останній рядок таблиці (без b₀) відповідає значенню базисних змінних для відповідного кута симплекса. В комірці b₀ знаходиться значення цільової функції при базисному розв’язку.

Ідея розв’язку ЗЛП – перевести незалежні змінні в базис, користуючись наступними критеріями.

Критерій допустимості базиса:

якщо в останньому стовпці симплекс-таблиці немає від’ємних елементів крім, можливо, останнього, то відповідний цій таблиці базис допустимий ().

Критерій оптимальності таблиці:

якщо в останньому рядку немає додатніх елементів, крім, можливо, останнього, то відповідний цій таблиці базис оптимальний (). При цьому.

Критерій відсутності розв’язку:

якщо в симплекс-таблиці маємо такий стовпець, останній елемент якого додатній, а всі інші недодатні, то відповідна ЗЛП не має оптимального розв’язку ().

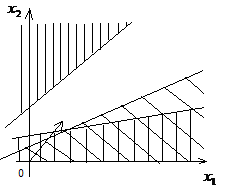
Критерій існування ведучого елемента:

якщо для даної симплекс-таблиці не задовольняється критерій оптимальності базиса та відсутності оптимального розв’язку, то в цій симплекс-таблиці існує ведучий елемент. Його знаходять в стовпці з найбільшим серед множинипо умові.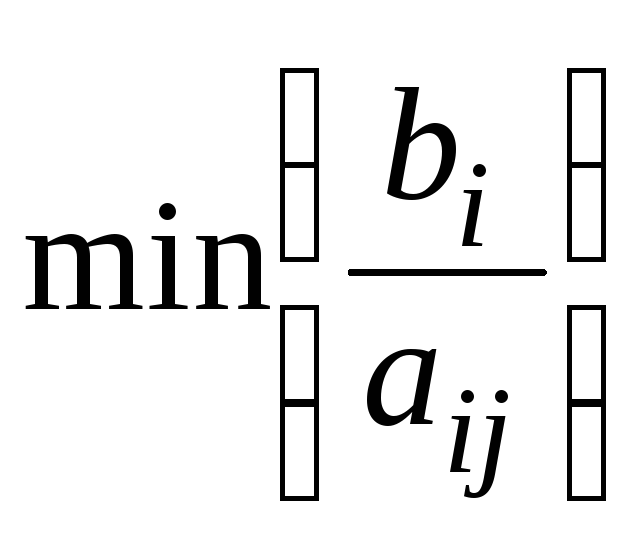

Тепер сформулюємо алгоритм правил перетворення симплекс-таблиці;

1. всі елементи рядка, на якому розміщений ведучий елемент, ділимо на нього (на місці ведучого елемента з’являється 1);

2. всі інші елементи ведучого стовпця заміняємо нулями;

3. всі інші елементи симплекс-таблиці перетворюємо по правилу прямокутника:

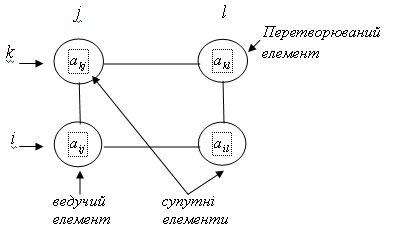
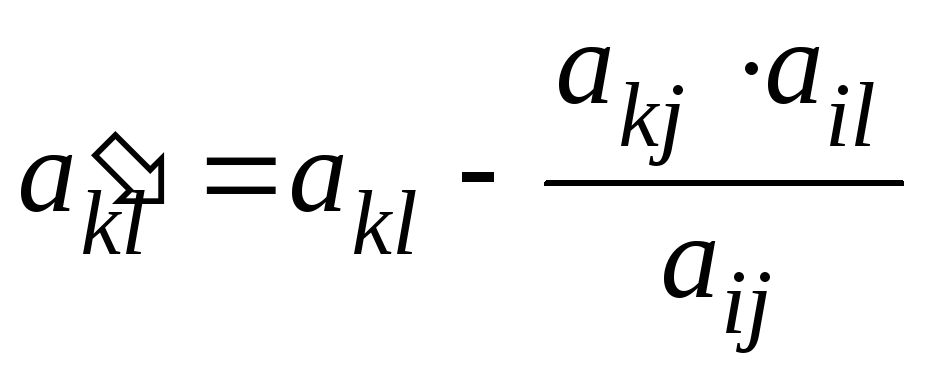
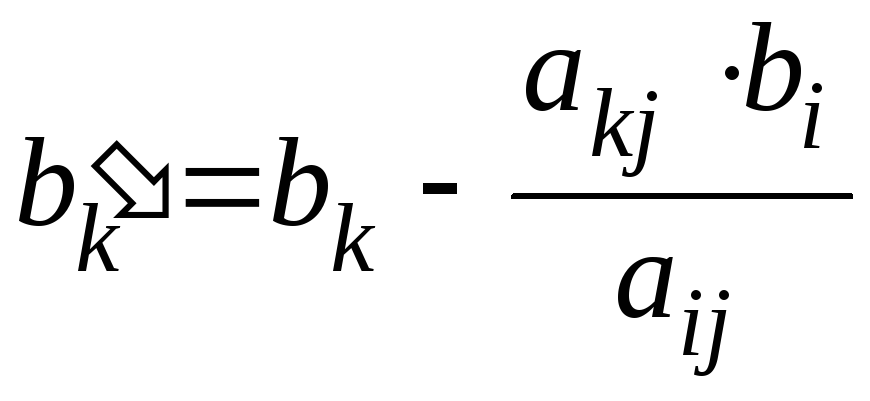
Тепер метод послідовного покращення плану або симплекс-метод можна представити так:

1. знаходимо будь-яке базисне рішення і складаємо симплекс-таблицю, відповідну цьому базису;

2. переглядаємо останній рядок таблиці, якщо в ньому немає додатніх елементів (крім, можливо 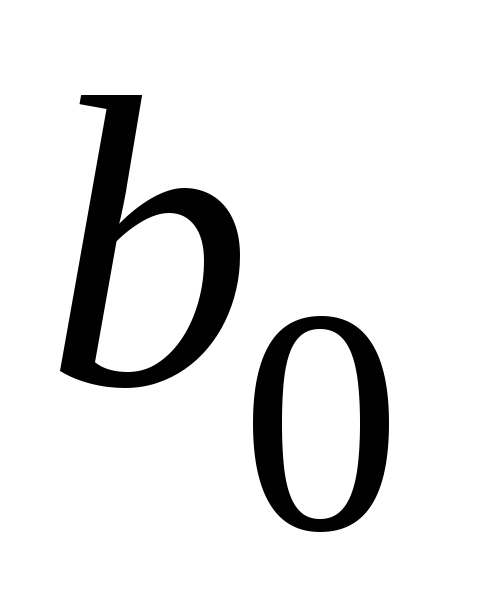) то оптимальне рішення знайдено –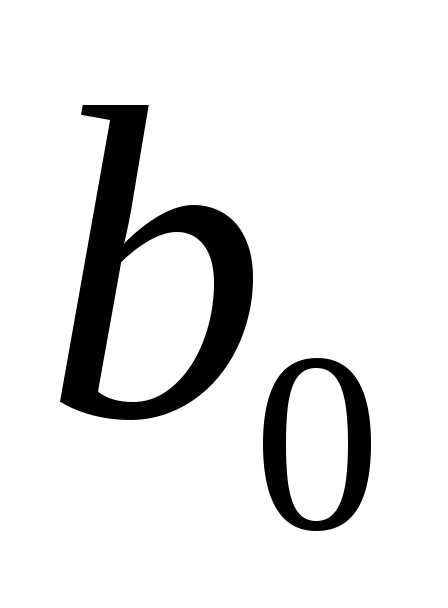буде мінімальним значенням;

3. якщо ж серед елементів останнього рядка є додатні елементи, але хоча б над одним із них є стовпець, що не вміщує інших додатніх елементів, то система немає розв’язку;

4. якщо обидва критерії (пункти 2, 3) не виконані, то вибирають ведучий елемент і перетворюють симплекс-таблицю.

Перейдемо до розрахунку попереднього прикладу.

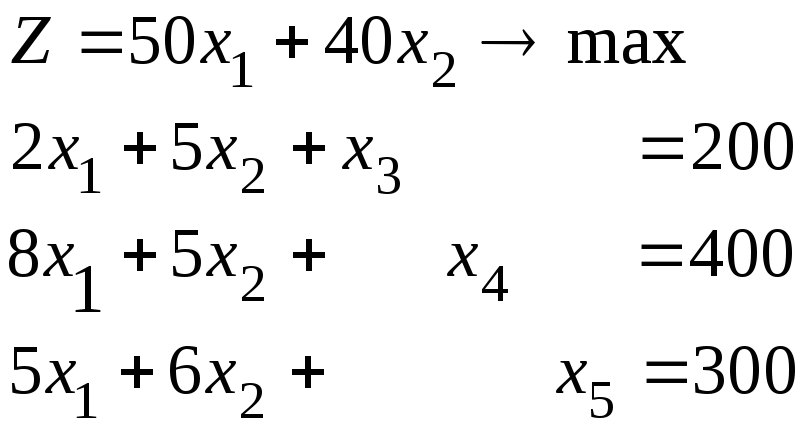
Складемо першу симплекс-таблицю:

Базис
	2	5	1	0	0	200
	8	5	0	1	0	400
	5	6	0	0	1	300
	50	40	0	0	0	0

Знаходимо ведучий елемент в стовпці

Отже, ведучий елемент . По відношенню до нього перетворюємо таблицю:

Базис
	0
	0
	0

Ця ж таблиця після виконання арифметичних дій:

Базис
	0	3,75	1	-0,25	0	100
	1	0,625	0	0,125	0	50
	0	2,875	0	-0,625	1	50
	0	8,75	0	-6,25	0	-2500

В новій таблиці в останньому рядку є додатній елемент .

Над ним знаходимо ведучий елемент таблиці .

Отже, ведучим елементом є .

Повторюємо перетворення таблиці:

Базис
	0	0	1	1,105	-1,304	34,78
	1	0	0	0,261	0,217	39,13
	0	1	0	-0,217	0,348	17,39
	0	0	0	-7,438	-3,043	-2640

Таблиця оптимальна. В ній відповідь: .