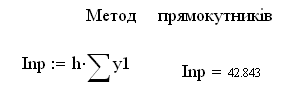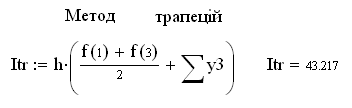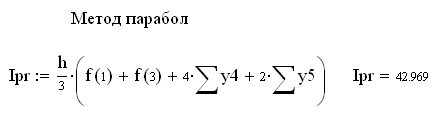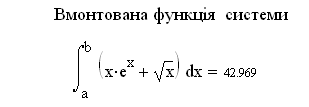- •Посібник з інформатики і системології
- •Тема 1. Використання текстового процесора Word в практичній роботі фахівця
- •1.1. Теоретична частина
- •1.2. Завдання для виконання лабораторної роботи
- •1.3 Приклад виконання роботи
- •1. Друкування та форматування тексту
- •2. Складання списків та їх форматування Кондитерська фабрика
- •3.Створення таблиці
- •4. Користування об’єктами WordArt
- •5. Створення формул
- •6. Складання блок-схеми
- •Питання для самоконтролю
- •Тема 2. Використання табличного процесора ms Excel в практичній роботі фахівця
- •2.1. Теоретична частина
- •2.2. Типи даних ет Excel
- •2.3. Сортування та фільтрація даних
- •2.4. Статистична обробка експериментальних даних на еп Excel (Завдання №1)
- •2.5. Завдання для виконання роботи
- •2.6. Приклад виконання роботи
- •2.7. Питання для самоконтролю
- •Тема 3. Алгоритмізація фахових задач та їх програмування на мові Pascal for Windows
- •3.1. Алгоритми
- •Фігури блок-схем
- •А) б)
- •3.2. Основи програмування на мові Pascal for Windows
- •3.3. Завдання для виконання лабораторної роботи
- •Завдання по темі
- •3.5. Питання для самоконтролю
- •Тема 4. Використання системи MathCad для розв’язування фахових задач
- •4.1. Загальні положення
- •4.2. Основи роботи в MathCad
- •1. Визначення змінних та їх результатів
- •4.3. Графічні об’єкти
- •В. Графічний вигляд функції
- •4.4. Символьний режим роботи
- •4.5. Завдання до виконання лабораторних робіт
- •Варіанти завдань
- •Варіанти до завдання 1
- •Варіанти до завдання 2
- •Варіанти до завдання 3
- •Варіанти завдання 4
- •Варіанти до завдання 5
- •4.6. Питання для самоконтролю
- •Тема 5. Розв’язування систем лінійних алгебраїчних рівнянь
- •5.1. Завдання до виконання роботи
- •Варіанти завдань
- •5.2. Питання для самоконтролю
- •Тема 6. Розв’язок нелінійних рівнянь та їх систем
- •6.1. Загальні положення
- •6.2. Етапи відокремлення коренів
- •6.3. Способи уточнення коренів
- •6.3.1. Метод половинного ділення (дихотомії)
- •6.3.2. Уточнення коренів методом хорд
- •6.3.3. Уточнення кореня методом дотичних (Ньютона)
- •6.3.4. Ітераційний метод уточнення кореня
- •6.3.5. Система нелінійних рівнянь
- •Варіанти завдань
- •6.4. Питання для самоконтролю
- •Тема 7. Інтерполяція і апроксимація функцій заданих таблично
- •7.1. Постановка задачі
- •7.2. Інтерполяційний поліном Лагранжа
- •7.3. Табличний метод застосування полінома Лагранжа
- •7.4. Інтерполяційні формули Ньютона
- •Перша інтерполяційна формула Ньютона
- •Друга інтерполяційна формула Ньютона
- •7.5. Обернена інтерполяція
- •Обернена інтерполяція
- •7.6. Апроксимація функцій методом найменших квадратів
- •7.7. Нелінійна апроксимація
- •Експоненціальна апроксимація
- •Варіанти завдань
- •7.9. Питання для самоконтролю
- •Тема 8. Чисельне диференціювання та інтегрування функцій
- •8.1. Наближене диференціювання
- •Диференціювання функції на базі
- •Варіанти завдань
- •8.3. Питання для самоконтролю
- •Тема 9: Чисельне інтегрування звичайних диференційних рівнянь
- •9.1. Загальні поняття
- •9.2. Метод Ейлера
- •9.3. Метод Рунге-Кутта
- •9.4. Інтегрування диференційних рівнянь інструментарієм системи MathCad
- •Функції rkfixed, Bulstoer таRkadapt
- •9.5. Завдання до виконання роботи
- •Варіанти завдань
- •9.6. Питання для самоконтролю
- •Тема 10. Чисельні методи оптимізації
- •10.1. Постановка задачі
- •10.2. Постановка задачі лінійного програмування
- •10.3. Геометрична інтерпретація злп
- •Графічний розв’язок злп
- •10.4. Симплекс-метод розв’язку злп
- •10.5. Розв’язок злп з допомогою ms Excel
- •Варіанти завдань
- •10.6. Транспортна задача
- •10.6.1. Постановка задачі
- •10.6.2. Метод північно-західного кута
- •Варіанти транспортної задачі
- •10.7. Питання для самоконтролю
- •Тема 11. Власні значення та власні вектори
- •11.1. Загальні поняття
- •11.2. Власні значення
- •11.3 Власні вектори
- •11.4 Знаходження найбільшого власного числа
- •11.5 Завдання
- •Варіанти завдань
- •11.6 Питання для самоперевірки
- •Література
- •Тема 1. Використання текстового процесора Word в практичній роботі фахівця 4
Тема 8. Чисельне диференціювання та інтегрування функцій
8.1. Наближене диференціювання
При
розв’язуванні практичних задач часто
приходиться знаходити похідну для
функцій, заданих таблично. В цьому
випадку замінюють одну функцію
![]() на деякому відрізку
на деякому відрізку![]() апроксимуючою або інтерполюючою функцією
апроксимуючою або інтерполюючою функцією![]() і потім вважають, що
і потім вважають, що![]() .
.
Аналогічно поступають і для знаходження похідних вищого порядку.
Потрібно
відмітити, що чисельне диференціювання
являє собою операцію менш точну, ніж
операції інтерполяції та апроксимації.
Дійсно, близькість координат функції
![]() та
та![]() зовсім не гарантують, що дотичні до їх
графіків на відрізку
зовсім не гарантують, що дотичні до їх
графіків на відрізку![]() будуть давати таку ж близькість (рисунок
30).
будуть давати таку ж близькість (рисунок
30).
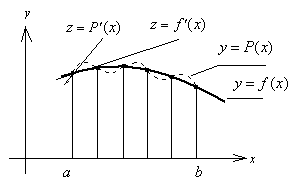
Рисунок 30 - Похибки в обчисленні похідних
Інколи,
через складності аналітичного виразу
![]() застосування попереднього методу є не
ефективним. В цьому випадку застосовують
чисельне диференціювання, що базується
на першій інтерполяційній формулі
Ньютона:
застосування попереднього методу є не
ефективним. В цьому випадку застосовують
чисельне диференціювання, що базується
на першій інтерполяційній формулі
Ньютона:
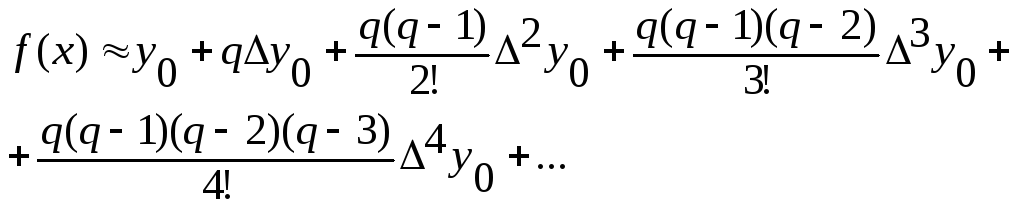
Перемноживши біноми, будемо мати:
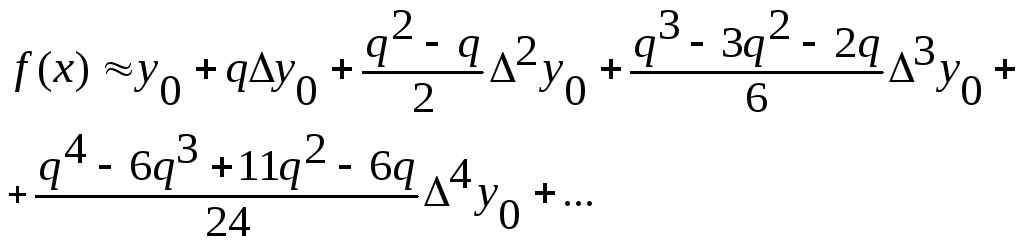
Так
як
![]() (
(![]()
![]()
![]()
![]() ),
маємо:
),
маємо:
![]() .
(8.1)
.
(8.1)
Якщо
![]() ще раз продиференціювати, будемо мати:
ще раз продиференціювати, будемо мати:
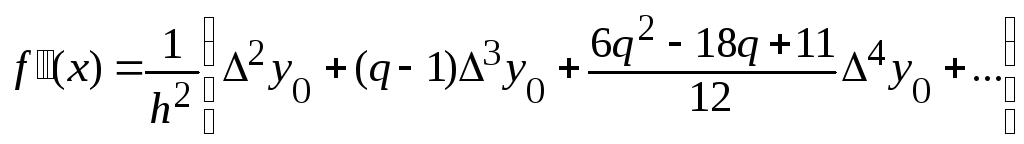 ,
(8.2)
,
(8.2)
так
як
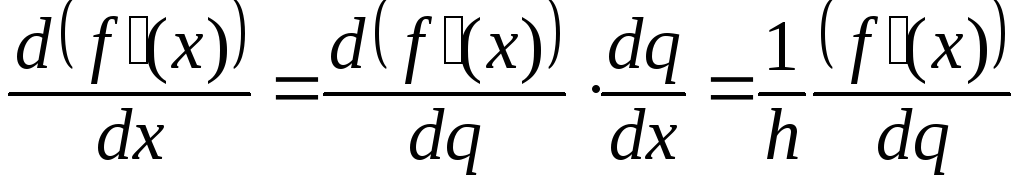 .
.
Якщо похідну потрібно знайти в точках інтерполяції формули (8.1) та (8.2) значно спрощуються
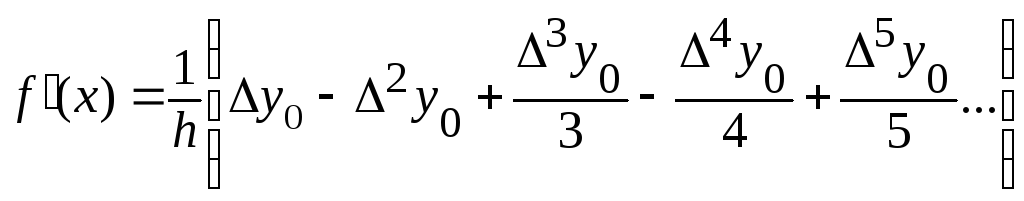 (8.3)
(8.3)
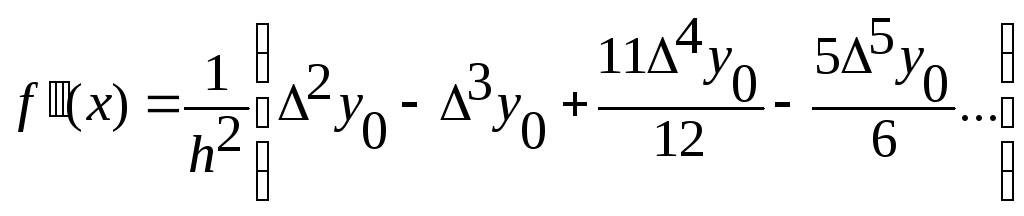 (8.4).
(8.4).
Приклад:
Диференціювання функції на базі
інтерполяційної формули Ньютона


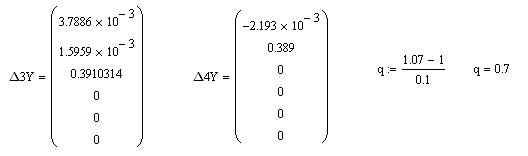


Кубічна апроксимація

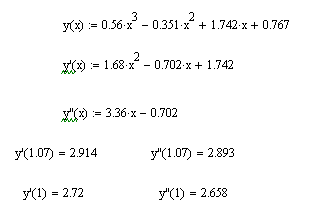
З допомогою MathCad:

8.2. Наближене інтегрування функції
В
класичній математиці визначений інтеграл
неперервної на відрізку
![]() функції
функції![]() визначається по формулі Ньютона-Лейбніца
визначається по формулі Ньютона-Лейбніца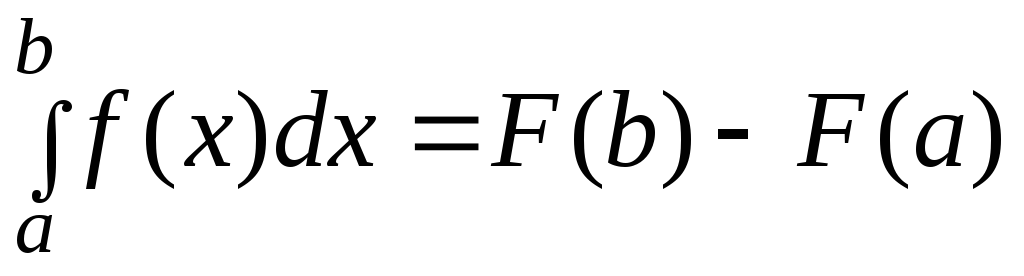 ,
де
,
де![]() – первісна для функції
– первісна для функції![]() ,
тобто
,
тобто![]() .
.
Однак
в реальних фахових задачах первісна
функція
![]() знаходиться з великими труднощами, а
часто її взагалі неможливо знайти.
Більше того, якщо функція задана таблично,
тоді саме поняття первісної взагалі
втрачає зміст.
знаходиться з великими труднощами, а
часто її взагалі неможливо знайти.
Більше того, якщо функція задана таблично,
тоді саме поняття первісної взагалі
втрачає зміст.
В
цих випадках фахівцю на допомогу
приходять чисельні методи одержання
визначеного інтегралу. Формули, по яким
здійснюється знаходження
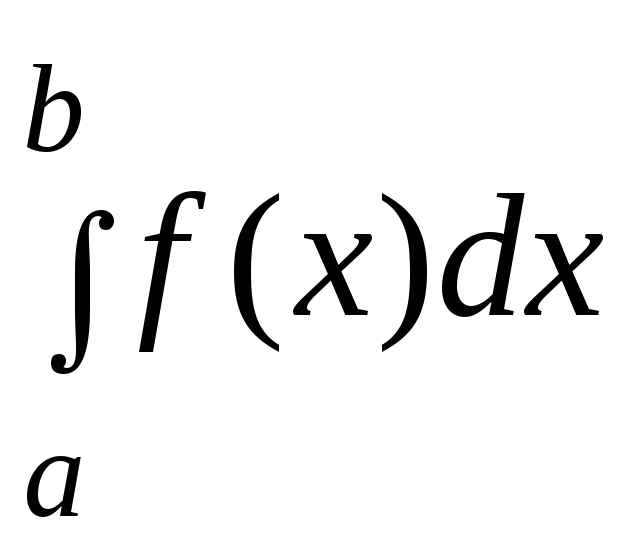 випливають із геометричної інтерпретації
інтегралу: значення визначеного інтегралу
чисельно дорівнює площі криволінійної
трапеції, обмеженою відрізком
випливають із геометричної інтерпретації
інтегралу: значення визначеного інтегралу
чисельно дорівнює площі криволінійної
трапеції, обмеженою відрізком![]() на осіОХ,
ординатами f(a)
та f(b)
та графіком функції
на осіОХ,
ординатами f(a)
та f(b)
та графіком функції
![]() .
.
Біда лише в тому, що в геометрії немає точної формули для визначення площі криволінійної трапеції. Тому їх знаходять наближено, як суму площ елементарних фігур, для яких формули знаходження площ відомі. Такі формули називаються квадратурними формулами. Розглянемо деякі з них.
8.2.1. Метод прямокутників
Розіб’ємо
діапазон
![]() наn
рівномірних частин. Тоді величина
наn
рівномірних частин. Тоді величина
![]() називається кроком інтегрування.
називається кроком інтегрування.
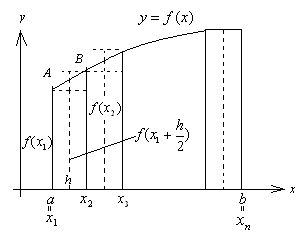
Рисунок 31 – Формула прямокутників
Тоді
кожний прямокутник буде мати площу:
![]() .
Якщо за
.
Якщо за![]() брати ліву або праву бічну сторону
будемо мати площу з надлишком або з
недостачею. Більш того, будемо мати
елементарну площу прямокутника наближену
до елементарної криволінійної трапеції.
брати ліву або праву бічну сторону
будемо мати площу з надлишком або з
недостачею. Більш того, будемо мати
елементарну площу прямокутника наближену
до елементарної криволінійної трапеції.
Якщо
![]() візьмемо на середині кроку інтегрування.
Тоді формула прямокутників одержання
визначеного інтегралу буде мати
структуру:
візьмемо на середині кроку інтегрування.
Тоді формула прямокутників одержання
визначеного інтегралу буде мати
структуру:
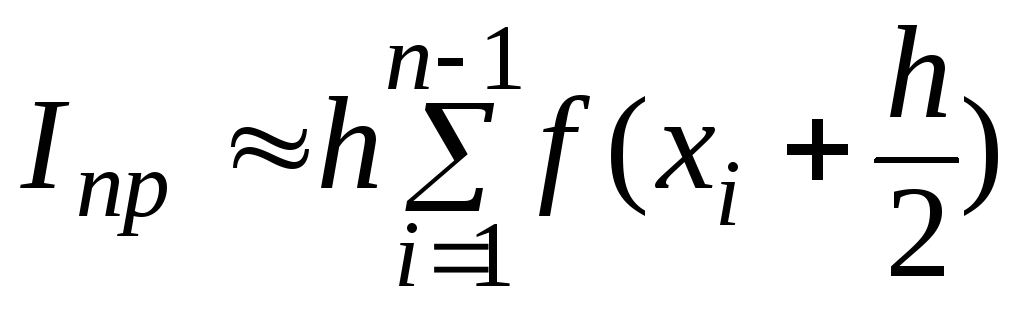 (8.5)
(8.5)
8.2.2. Метод трапецій
Замінимо
дугу АВ
(рисунок 31) графіка підінтегральної
функції хордою і визначимо площу
елементарної трапеції
![]() .
.
Ї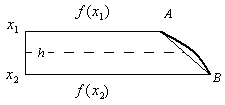 ї
площа буде
ї
площа буде![]() .
.
Поширюючи цей вираз на всю площу криволінійної трапеції будемо мати:
![]() або
в стислому вигляді:
або
в стислому вигляді:
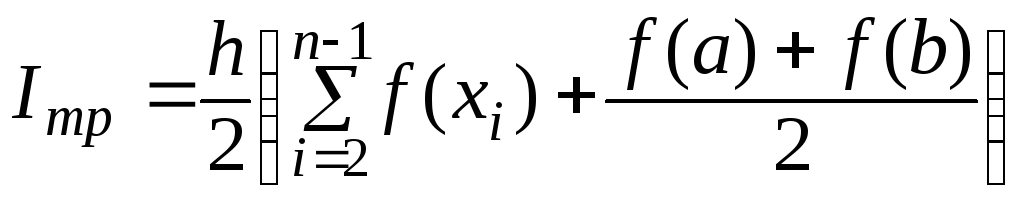 .
(8.6)
.
(8.6)
8.2.3. Метод парабол (Сімпсона)
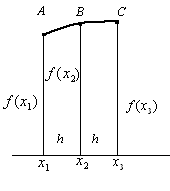
Розіб’ємо
діапазон інтегрування на
![]() частин. Тоді через три точки
частин. Тоді через три точки![]() ,
що являють собою ординати
,
що являють собою ординати![]() ,
,![]() та
та![]() можна провести єдину параболу, графік
якої практично співпаде з графіком
можна провести єдину параболу, графік
якої практично співпаде з графіком![]() на діапазоні
на діапазоні![]() .
.
Площа такої елементарної параболічної трапеції можна вирахувати за формулою:
![]()
Або в більш компактному вигляді:
![]()
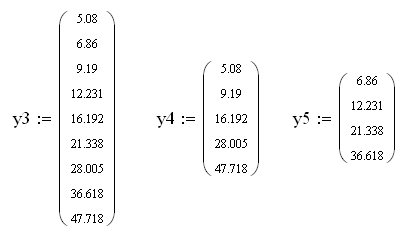
Приклад:

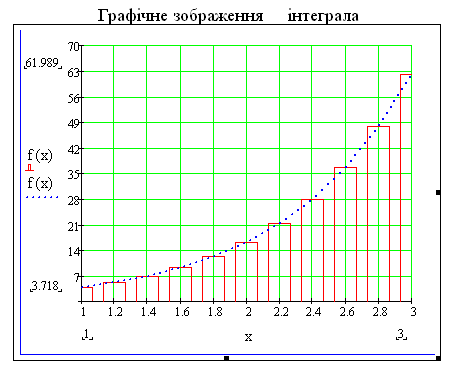
Значення функції