7.3. Табличний метод застосування полінома Лагранжа

В деяких випадках зручніше інтерполяційні значення визначати в табличній формі. Для цього створюють таблицю:

	j
i					…
					…
					…
					…
	…	…	…	…	…	…	…
					…

В цьому випадку поліном Лагранжа має вигляд

,

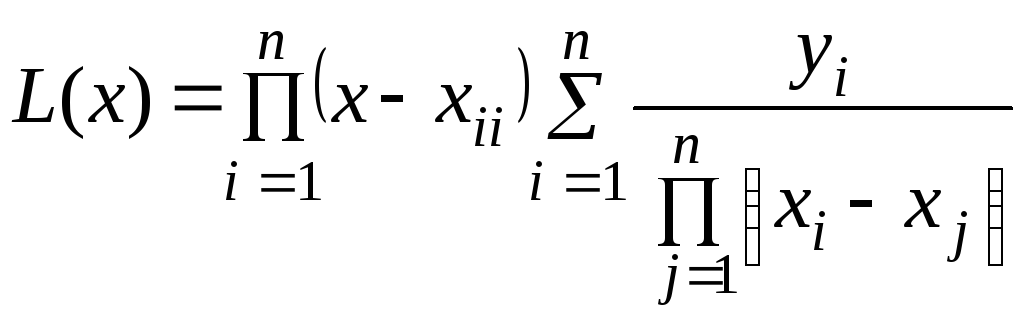де – добуток усіх діагональних елементів таблиці;

–і-те значення табличної функції;

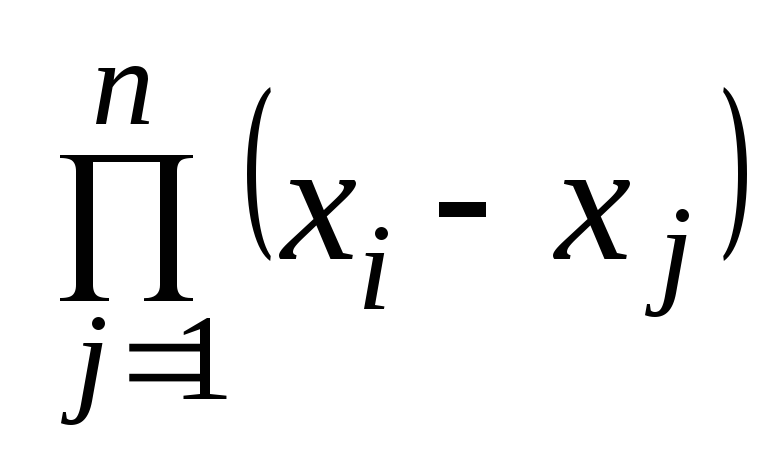–добуток усіх елементів і-го рядка таблиці, включаючи також і діагональний елемент.

Застосуємо цей метод для попередньої задачі:

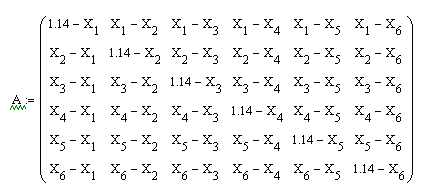
7.4. Інтерполяційні формули Ньютона

Якщо в табличній функції вузли інтерполяції рівновіддалені, тобто , то при інтерполюванні можна застосувати менш громіздкий математичний апарат, який описується інтерполяційними формулу Ньютона. Величинаh називається кроком інтерполяції.

Вияснимо спочатку поняття кінцевих різниць.

Нехай задана функція . Тодіназиваєтьсяпершою кінцевою різницею.

Аналогічно, кінцева різниця другого порядку (читається «дельта два ігрек»):

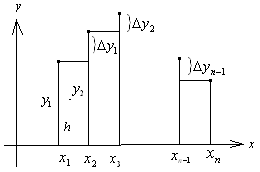
і т.д. (рисунок 28).

					…
					…
					…
					…
					…
…	…	…	…	…	…

Рисунок 28 – Кінцеві різниці функції

Тоді перша інтерполяційна формула Ньютона має вигляд:

(7.4)

Застосовується вона для інтерполяції табличної функції в верхній частині таблиці. В ній фаза інтерполяції визначає скільки кроківпотрібно зробити, для переходу із точкив точкух. Застосуємо формулу (7.4) для визначення .

Перша інтерполяційна формула Ньютона

Як видно з цього прикладу кінцеві різниці вищих порядків в нижній частині таблиці зникають. Тому приведена формула не може бути застосована для х в цій частині таблиці. Тут працює друга інтерполяційна формула Ньютона, яка має вигляд:

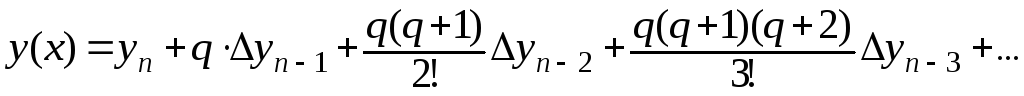(7.5)

Величина для неї розраховується по виразу.

Покажемо застосування формули (7.5) для значення (екстраполяція):

Друга інтерполяційна формула Ньютона

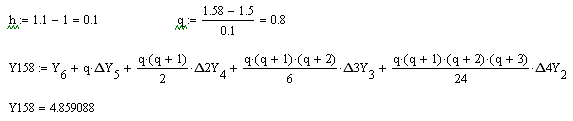
7.5. Обернена інтерполяція

Задача оберненої інтерполяції полягає в тому, щоб по заданому значенню функції у визначити відповідне їй значення аргументу х.

Припустимо, що функція монотонна і значенняу знаходиться між та. Замінимо функціюу першою інтерполяційною функцією Ньютона:

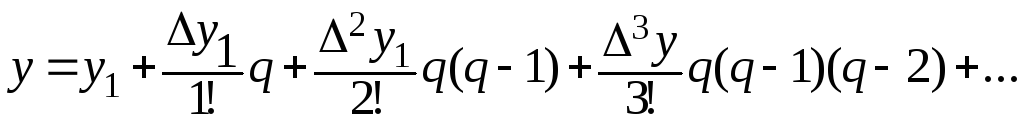(7.6)

Побудуємо ітераційний процес знаходження значення в відповідності з інтерполяційним методом уточнення кореня нелінійного рівняння (рисунок 25):

звідси:

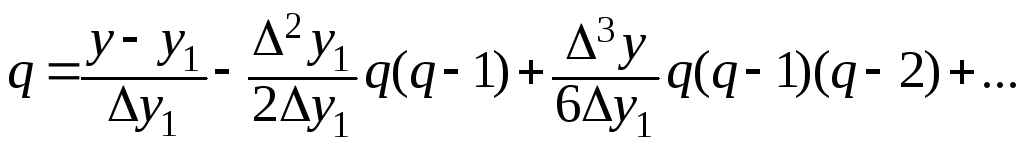
Початкове значення знайдемо із скороченого значення виразу:

.

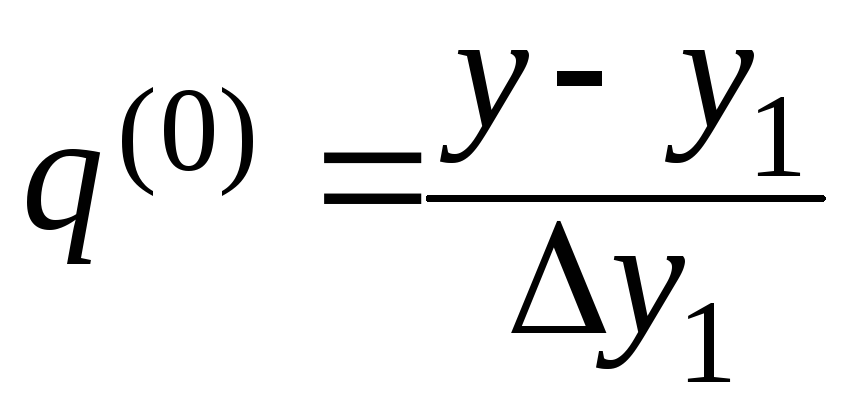Далі створюємо ітераційний процес: ;і т.д. допоки не установляться цифри величинив відповідності з заданою точністю.

Значення шуканого аргументу знаходять з формули: . Тобто.

Приклад. Для даних попередньої задачі знайти х при якому .