- •Посібник з інформатики і системології
- •Тема 1. Використання текстового процесора Word в практичній роботі фахівця
- •1.1. Теоретична частина
- •1.2. Завдання для виконання лабораторної роботи
- •1.3 Приклад виконання роботи
- •1. Друкування та форматування тексту
- •2. Складання списків та їх форматування Кондитерська фабрика
- •3.Створення таблиці
- •4. Користування об’єктами WordArt
- •5. Створення формул
- •6. Складання блок-схеми
- •Питання для самоконтролю
- •Тема 2. Використання табличного процесора ms Excel в практичній роботі фахівця
- •2.1. Теоретична частина
- •2.2. Типи даних ет Excel
- •2.3. Сортування та фільтрація даних
- •2.4. Статистична обробка експериментальних даних на еп Excel (Завдання №1)
- •2.5. Завдання для виконання роботи
- •2.6. Приклад виконання роботи
- •2.7. Питання для самоконтролю
- •Тема 3. Алгоритмізація фахових задач та їх програмування на мові Pascal for Windows
- •3.1. Алгоритми
- •Фігури блок-схем
- •А) б)
- •3.2. Основи програмування на мові Pascal for Windows
- •3.3. Завдання для виконання лабораторної роботи
- •Завдання по темі
- •3.5. Питання для самоконтролю
- •Тема 4. Використання системи MathCad для розв’язування фахових задач
- •4.1. Загальні положення
- •4.2. Основи роботи в MathCad
- •1. Визначення змінних та їх результатів
- •4.3. Графічні об’єкти
- •В. Графічний вигляд функції
- •4.4. Символьний режим роботи
- •4.5. Завдання до виконання лабораторних робіт
- •Варіанти завдань
- •Варіанти до завдання 1
- •Варіанти до завдання 2
- •Варіанти до завдання 3
- •Варіанти завдання 4
- •Варіанти до завдання 5
- •4.6. Питання для самоконтролю
- •Тема 5. Розв’язування систем лінійних алгебраїчних рівнянь
- •5.1. Завдання до виконання роботи
- •Варіанти завдань
- •5.2. Питання для самоконтролю
- •Тема 6. Розв’язок нелінійних рівнянь та їх систем
- •6.1. Загальні положення
- •6.2. Етапи відокремлення коренів
- •6.3. Способи уточнення коренів
- •6.3.1. Метод половинного ділення (дихотомії)
- •6.3.2. Уточнення коренів методом хорд
- •6.3.3. Уточнення кореня методом дотичних (Ньютона)
- •6.3.4. Ітераційний метод уточнення кореня
- •6.3.5. Система нелінійних рівнянь
- •Варіанти завдань
- •6.4. Питання для самоконтролю
- •Тема 7. Інтерполяція і апроксимація функцій заданих таблично
- •7.1. Постановка задачі
- •7.2. Інтерполяційний поліном Лагранжа
- •7.3. Табличний метод застосування полінома Лагранжа
- •7.4. Інтерполяційні формули Ньютона
- •Перша інтерполяційна формула Ньютона
- •Друга інтерполяційна формула Ньютона
- •7.5. Обернена інтерполяція
- •Обернена інтерполяція
- •7.6. Апроксимація функцій методом найменших квадратів
- •7.7. Нелінійна апроксимація
- •Експоненціальна апроксимація
- •Варіанти завдань
- •7.9. Питання для самоконтролю
- •Тема 8. Чисельне диференціювання та інтегрування функцій
- •8.1. Наближене диференціювання
- •Диференціювання функції на базі
- •Варіанти завдань
- •8.3. Питання для самоконтролю
- •Тема 9: Чисельне інтегрування звичайних диференційних рівнянь
- •9.1. Загальні поняття
- •9.2. Метод Ейлера
- •9.3. Метод Рунге-Кутта
- •9.4. Інтегрування диференційних рівнянь інструментарієм системи MathCad
- •Функції rkfixed, Bulstoer таRkadapt
- •9.5. Завдання до виконання роботи
- •Варіанти завдань
- •9.6. Питання для самоконтролю
- •Тема 10. Чисельні методи оптимізації
- •10.1. Постановка задачі
- •10.2. Постановка задачі лінійного програмування
- •10.3. Геометрична інтерпретація злп
- •Графічний розв’язок злп
- •10.4. Симплекс-метод розв’язку злп
- •10.5. Розв’язок злп з допомогою ms Excel
- •Варіанти завдань
- •10.6. Транспортна задача
- •10.6.1. Постановка задачі
- •10.6.2. Метод північно-західного кута
- •Варіанти транспортної задачі
- •10.7. Питання для самоконтролю
- •Тема 11. Власні значення та власні вектори
- •11.1. Загальні поняття
- •11.2. Власні значення
- •11.3 Власні вектори
- •11.4 Знаходження найбільшого власного числа
- •11.5 Завдання
- •Варіанти завдань
- •11.6 Питання для самоперевірки
- •Література
- •Тема 1. Використання текстового процесора Word в практичній роботі фахівця 4
6.4. Питання для самоконтролю
Типи нелінійних рівнянь.
Що таке корінь нелінійного рівняння?
Геометрична інтерпретація кореня нелінійного рівняння.
Два критерії існування відокремленого кореня на інтервалі
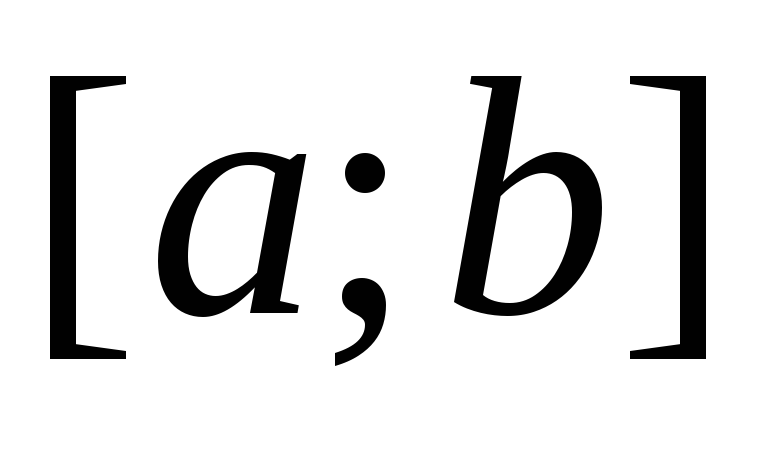 .
.Два етапи одержання коренів.
Аналітичний метод відокремлення коренів.
Режим табулювання функцій.
Графічний метод відокремлення коренів.
Метод половинного ділення.
Критерій виходу із ітераційного процесу.
Уточнення коренів методом хорд.
Виведення ітераційної формули методу хорд.
Уточнення кореня методом дотичних.
Виведення ітераційної формули метода Ньютона.
Критерії вибору точки застосування методу дотичних.
Ітераційний метод уточнення коренів.
Умова збіжності ітераційного методу.
Що таке коливний ітераційний процес?
Що таке монотонний ітераційний процес?
Способи запису СНР.
Ітераційна формула розв’язку СНР простою ітерацією.
Умова збіжності простої ітерації.
Виведення ітераційної формули методу Ньютона.
Що таке зона збіжності?
Що собою являє матриця Якобі?
Тема 7. Інтерполяція і апроксимація функцій заданих таблично
7.1. Постановка задачі
Фахівцю
в своїй діяльності часто приходиться
мати справу з функціями, що задані
таблично. Це дані експерименту,
спостережень, складні і громіздкі
аналітичні залежності, таблиці
автоматизованого проектування тощо.
На рисунку 27 в загальному вигляді
представлена така функція та її
інтерпретація на координатній площині.
Аргументи такої функції
![]() називаються вузлами інтерполяції.
називаються вузлами інтерполяції.
|
X |
x1 |
x2 |
… |
xi |
… |
xn |
|
Y |
y1 |
y2 |
… |
yi |
… |
yn |
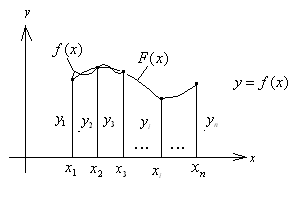
Рисунок – 27. Функція в табличному та графічному виглядах
При
роботі з такими даними приходиться
знаходити значення функції у
в точках аргументу х,
відмінних від вузлів інтерполяції. Така
операція називається інтерполяцією
функції. При цьому розрізняють інтерполяцію
в вузькому сенсі,
якщо
![]() ,
тобто значення функції шукають у
внутрішньому діапазоні таблиці, таекстраполяцією,
якщо функцію потрібно знайти за межами
інтервалу
,
тобто значення функції шукають у
внутрішньому діапазоні таблиці, таекстраполяцією,
якщо функцію потрібно знайти за межами
інтервалу
![]() .
.
В
цьому випадку шукану функцію
![]() заміняють аналітичною функцією
заміняють аналітичною функцією![]() ,
яка була б деякою мірою близькою до
,
яка була б деякою мірою близькою до![]() і, разом з тим, просто обчислювалась.
Така функція називаєтьсяапроксимуючою
(наближеною).
і, разом з тим, просто обчислювалась.
Така функція називаєтьсяапроксимуючою
(наближеною).
На практиці найчастіше використовують такі види апроксимуючих функцій:
Алгебраїчні поліноми степені n
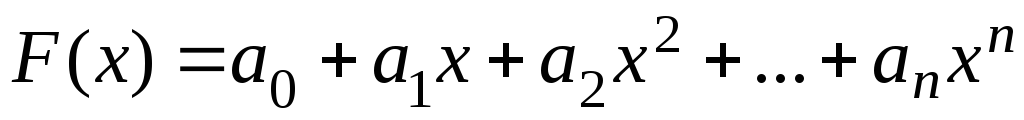 .
Цей метод має очевидні переваги. Поліноми
легко обчислювати, додавати, віднімати,
перемножувати, зручно диференціювати
та інтегрувати.
.
Цей метод має очевидні переваги. Поліноми
легко обчислювати, додавати, віднімати,
перемножувати, зручно диференціювати
та інтегрувати.Тригонометричні ряди виду:
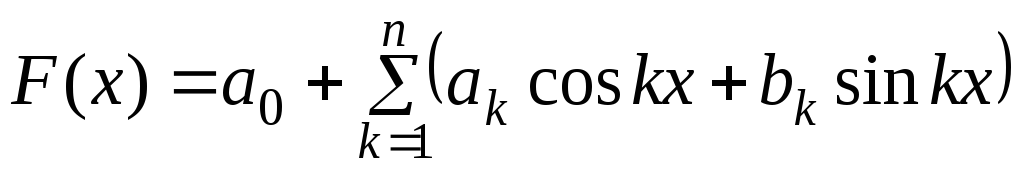 .
Така апроксимація особливо зручна,
коли функція
.
Така апроксимація особливо зручна,
коли функція періодична.
періодична.Дробово-раціональні функції
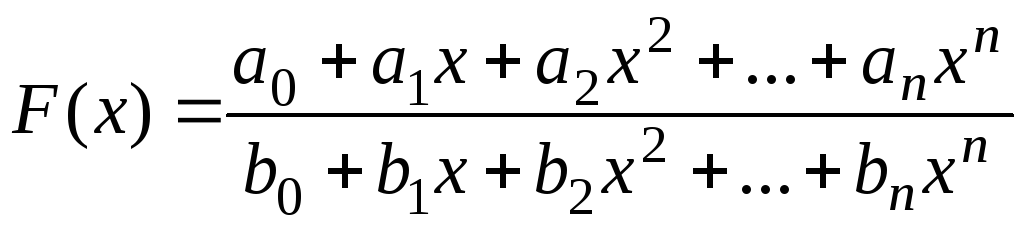 .
Цей вид функцій найчастіше використовують
для апроксимації результатів дослідів,
здобутих статистичним способом.
.
Цей вид функцій найчастіше використовують
для апроксимації результатів дослідів,
здобутих статистичним способом.Функції довільного вигляду (
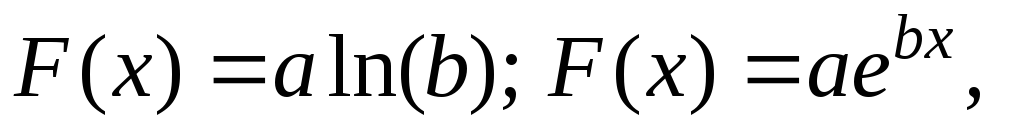
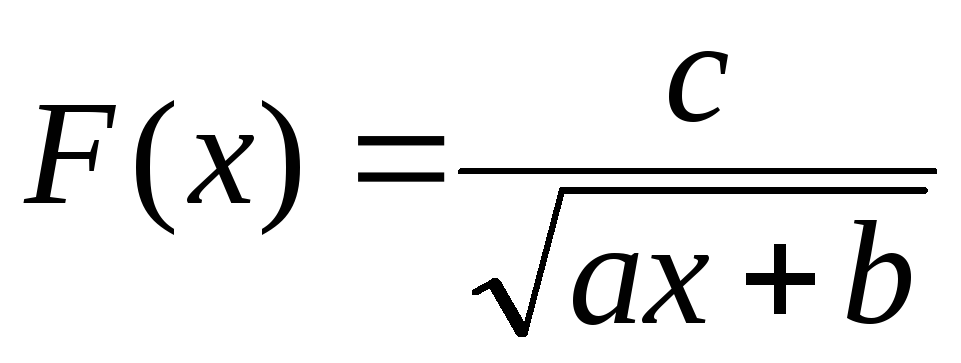 і т.д.), які б найбільш точно відповідали
розміщенню точок
і т.д.), які б найбільш точно відповідали
розміщенню точок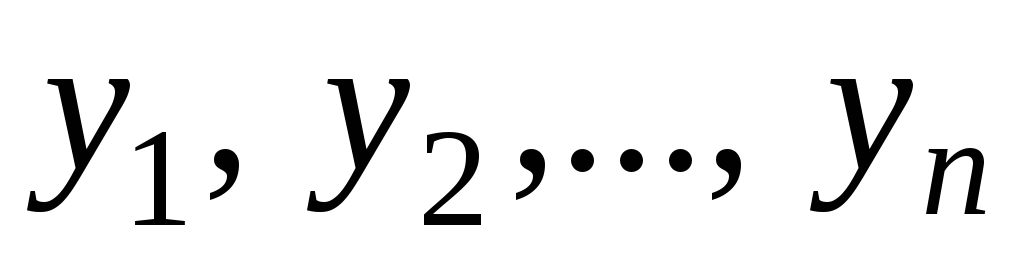 на координатній площині.
на координатній площині.
7.2. Інтерполяційний поліном Лагранжа
Розглянемо
апроксимацію функції
![]() таким поліномом
таким поліномом![]() ,
графік якого обов’язково проходив би
через всі табличні точки (див. рисунок
27). Тобто
,
графік якого обов’язково проходив би
через всі табличні точки (див. рисунок
27). Тобто![]() .
Для виведення формули такого полінома
розглянемо спочатку допоміжну задачу:
побудуємо спочатку поліном такий, що
.
Для виведення формули такого полінома
розглянемо спочатку допоміжну задачу:
побудуємо спочатку поліном такий, що![]() при
при![]() та
та![]() .
Ці умови можна записати так
.
Ці умови можна записати так

Такий поліном може мати вигляд:
![]() .
(7.1)
.
(7.1)
Якщо
![]() і враховуючи, що
і враховуючи, що![]() ,
маємо:
,
маємо:
![]() .
Звідси довільний коефіцієнт:
.
Звідси довільний коефіцієнт:
![]() .
Підставивши
.
Підставивши![]() в (7.1), маємо:
в (7.1), маємо:
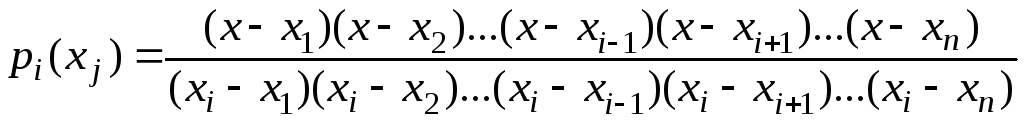 .
(7.3)
.
(7.3)
Дійсно
для всіх точок таблиці, за виключенням
![]() ,
цей поліном перетворюється в нуль. І
лише при
,
цей поліном перетворюється в нуль. І
лише при![]() його чисельник дорівнює знаменнику,
тобто
його чисельник дорівнює знаменнику,
тобто![]() .
.
Тепер
перейдемо до розв’язку початкової
задачі. В кожній точці
![]() таблиці, маємо не 1, а
таблиці, маємо не 1, а![]() .
Тобто значення знайденого полінома
(7.3) потрібно помножити на
.
Тобто значення знайденого полінома
(7.3) потрібно помножити на![]() .
Отже, шуканий поліном, який називається
поліномом Лагранжа і позначається
першою літерою його прізвища
.
Отже, шуканий поліном, який називається
поліномом Лагранжа і позначається
першою літерою його прізвища![]() буде мати вигляд:
буде мати вигляд:
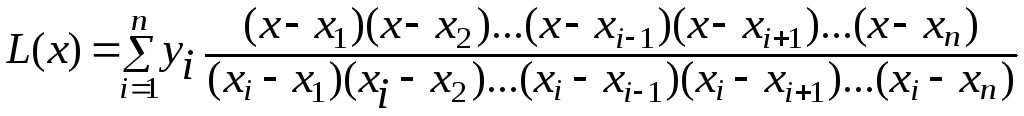 .
.
Для реалізації в системі MathCad цю формулу можна представити:
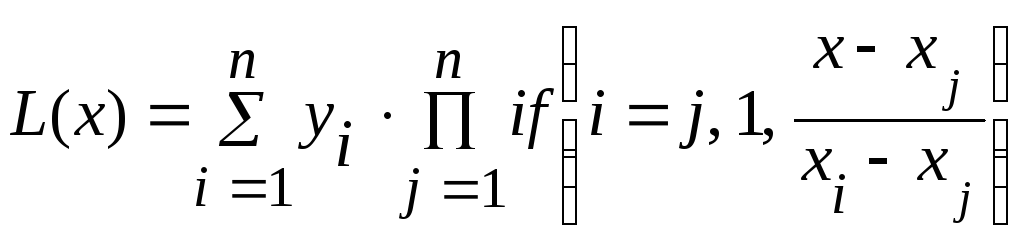 .
.
Приклад
використання
![]()