2.6. Приклад виконання роботи

Створення таблиці

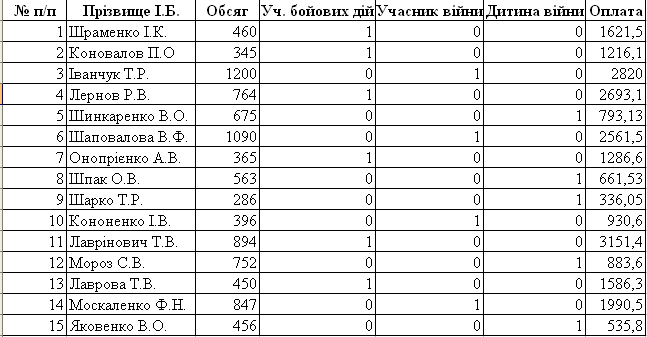
Створення таблиці (формули)

Сортування в бік зменшення обсягу спожитого газу

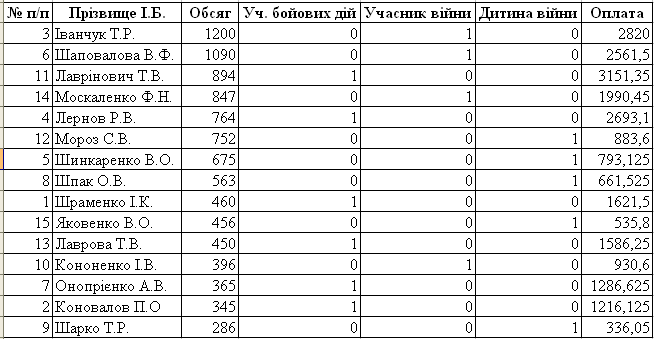
Фільтрування по букві «Ш»

Графік по обсягу та оплаті

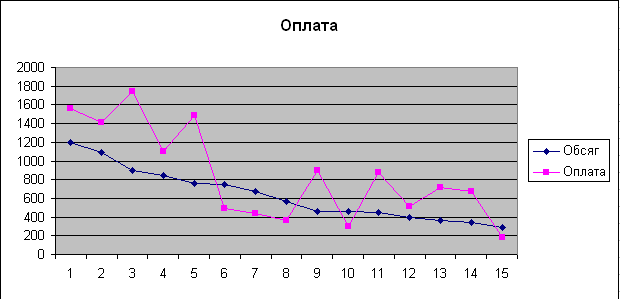
Використання функцій Excel для розрахунків.

Приклад обробки числових даних

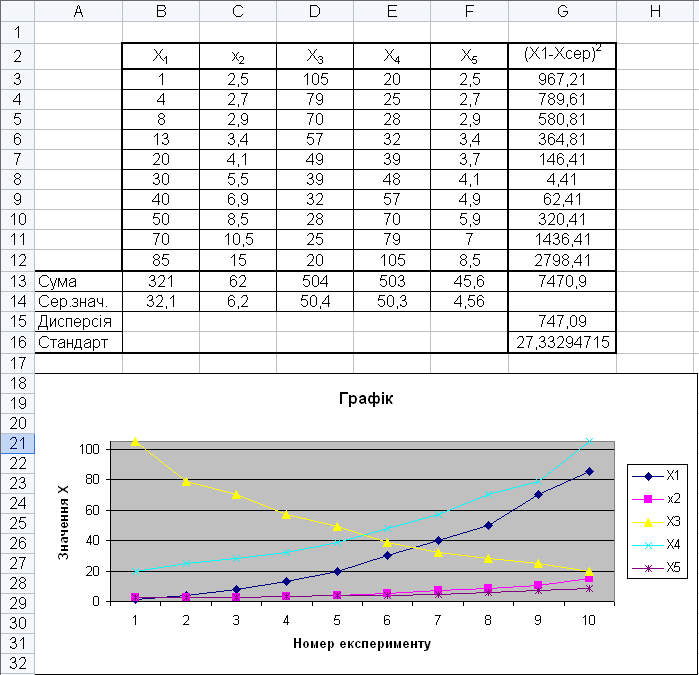
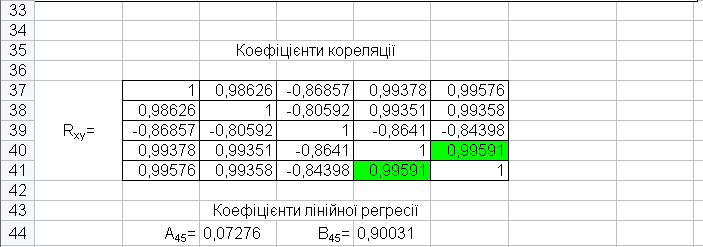
Графічний аналіз отриманих результатів

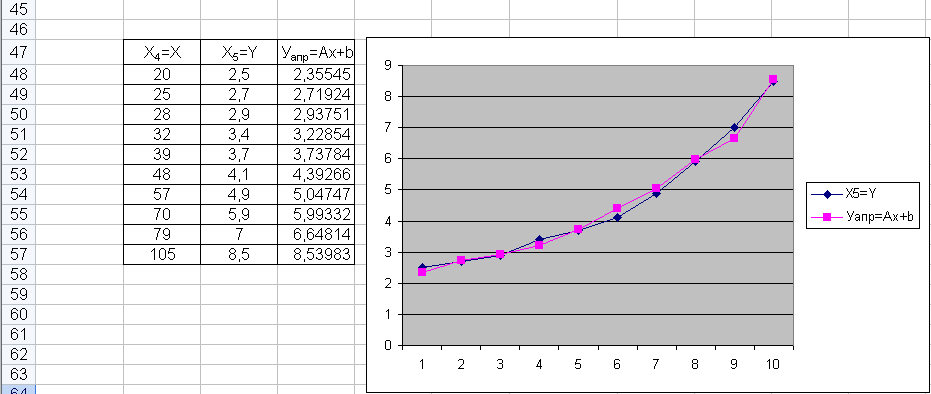
Дії з числами за допомогою функцій Excel (формули)

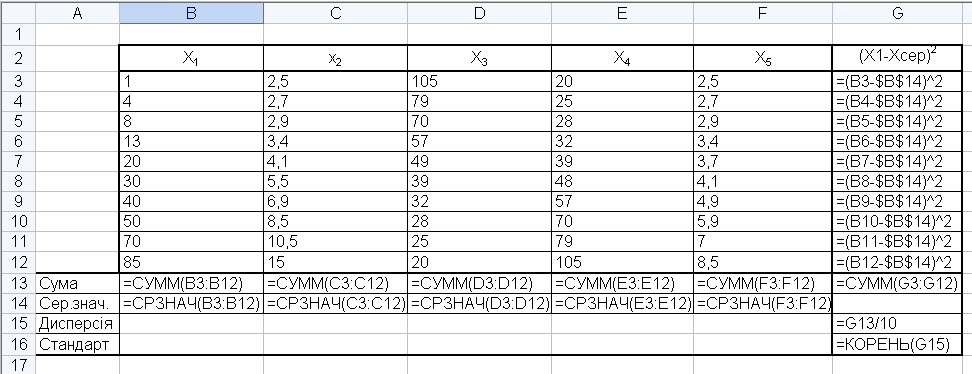
Коефіцієнти кореляції (формули)

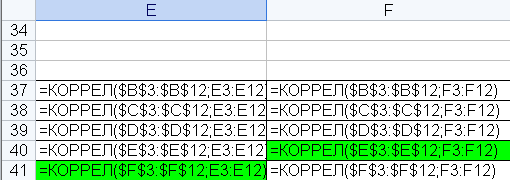
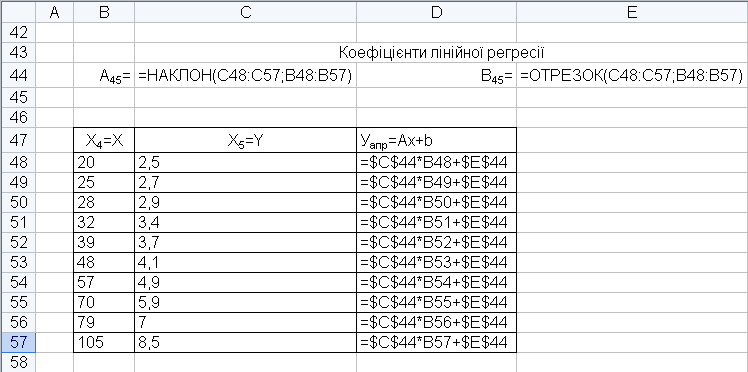
2.7. Питання для самоконтролю

1. Призначення ЕП Excel.

2. Як позначаються рядки і стовпці MS Excel?

3. Маркери в MS Excel.

4. Що таке робоча книга і робочий лист?

5. Як адресуються комірки таблиці?

6. Які види адрес комірок існують в ЕП Excel?

7. Які типи даних можуть бути занесені в комірку таблиці?

8. Як вводиться в комірку дійсне число і дата?

9. Як вставити (вилучити) порожній стовпець (рядок)?

10. Типи формул в ЕП Excel.

11. Які арифметичні дії можливі в формулах?

12. Як в активну комірку записати поточну дату (час)?

13. Як виконується логічна функція ЕСЛИ?

14. Результат дії логічних формул.

15. Результат дії текстових формул.

16. Як організувати в ЕП Excel графічний аналіз даних?

17. Які числові характеристики є в числовій послідовності?

18. Що таке дисперсія та стандарт?

19. Що таке коефіцієнт кореляції?

20. Що таке кореляційна матриця? Назвати її властивості.

21. Друкування формул в ЕП Excel.

22. Лінійна апроксимація.

23. Зміна форматів в комірці.

24. Як в MS Excel перейти з режиму формул в режим результатів і навпаки?

25. Додавання (вилучення) листів в MS Excel.

Тема 3. Алгоритмізація фахових задач та їх програмування на мові Pascal for Windows

3.1. Алгоритми

Алгоритм – це інструкція, яка дає можливість одержати з початкових даних бажаний результат.

Алгоритми можуть бути представлені словесно, у вигляді послідовності виконуваних формул, у вигляді геометричних фігур, тощо.

Алгоритм представлений геометричними фігурами називається блок-схемою. В блок-схемах фігури представляються у відповідності з ГОСТ–19.003-80, найбільш часто вживані фігури приведені у таблиці 5.

Розробка алгоритму – це найбільш творчий етап проектування, мета якого – створення послідовності дій комп’ютера в відповідності з умовами розв’язку задачі. При усій різноманітності структур алгоритмів можна виділити деякі типові їх елементи, із яких можна створити загальний алгоритм довільної складності. До них відносяться лінійний, розгалужений та циклічний процеси.

Фігури блок-схем

Таблиця 5

Назва блока	Зображення	Призначення	Напис в середині блока
Процес		Перетворення даних	Закон перетворення
Рішення		Розгалуження обчислювального процесу	Умова розгалуження
Введення, виведення		Введення або виведення даних незалежно від типу пристрою	Дія і перелік даних введення-виведення
Введення з клавіатури		Введення даних	Перелік змінних
Виведення на принтер		Виведення даних	Перелік змінних
Пуск, зупинка		Початок і кінець алгоритму	Текст, що відповідає початку та завершенню

Модифікація		Організація циклу	Параметри циклу (початкове, кінцеве значення та крок переадресації)
З’єднувачі		З’єднання ліній обчислювального процесу	Літери або літери з цифрами
Наперед визначений процес		Виклик підпрограми	Ім’я підпрограми
Виведення на екран монітора		Виведення даних	Перелік змінних

В лінійних обчислювальних процесах блоки алгоритма розміщуються строго послідовно і в такому ж порядку виконуються. Приклад такого алгоритму, по якому знаходиться площа трикутника за трьома сторонами (формула Герона), представлена на рисунку 2.

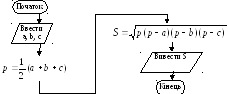
Рисунок 2 – Схема лінійного алгоритму

Залежно від того виконується чи ні якась умова, обчислювальний процес ведеться різними каналами блок-схеми, такий процес називається розгалуженим. На рисунку 3 представлений алгоритм розв’язку квадратного рівняння

При розв’язуванні багатьох задач бувають випадки коли необхідно виконати одні і ті ж обчислювальні дії багаторазово. Такі процеси називаються циклічними.

Щоб організувати цикл потрібно виконати такі дії:

1. до початку циклу задати початкове значення його параметру та виконати підготовчі операції;

2. після кожного виконання циклу збільшити на крок переадресації його параметр;

3. перевірити умову закінчення циклу і в залежності від цього закінчити цикл або його повторити.

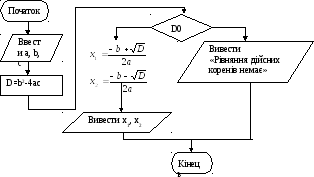
Ні Так

Рисунок 3 – Розгалужений обчислювальний процес

Циклічні процеси поділяються на цикли з невизначеною і визначеною кількістю повторень. В блок-схемах циклів з невизначеною кількістю повторень вихід із циклів реалізується з допомогою блока «рішення».

Всі неперервні функції (і т.д.), для заданого аргументух, на комп’ютері визначаються з допомогою нескінченного ряду, що являється розкладом цієї функції в ряд Тейлора (Маклорена). Реалізація такого визначення з заданою точністю здійснюється з допомогою циклу з невизначеною кількістю повторень. Для створення алгоритму розв’язку такої задачі пропонується така інструкція:

1. розписати ряд задавши 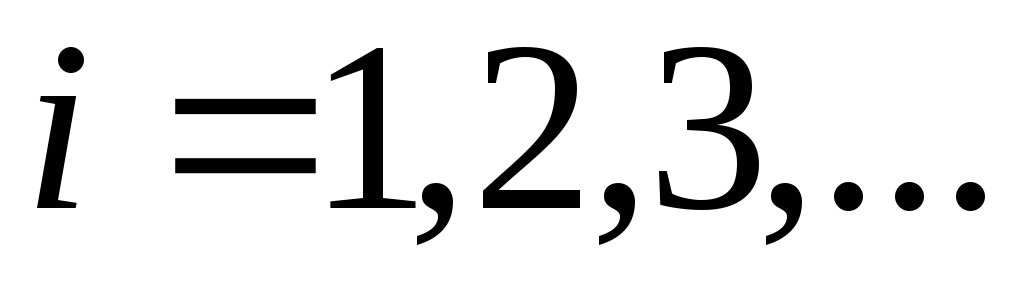до тих пір поки не стане зрозумілим закон зміни чисельника і знаменника поточного члена ряду;

2. визначити закон зміни чисельника поточного члена ряду;

3. визначити закон зміни знаменника поточного члена ряду;

4. визначити початкові дані для всіх змінних, що задіяні в розрахунку;

5. по даним попереднього аналізу побудувати алгоритм.

Приклад: знайти суму нескінченного ряду з точністю.

Дотримуємося інструкції:

1) ;

2) r=r*(-x)

3)

4) i=0; S=0; F=1; r=-1

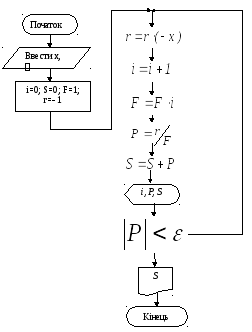
Блок-схема розв’язку задачі повинна мати вигляд:

Ні

Так

Рисунок 4 – Цикл з невизначеною кількістю повторень

Для обробки елементів масивів використовуються, як правило, цикли з визначеною кількістю повторень, які організуються з допомогою блока “модифікація”. В цьому блоці є два входи та два виходи. Початок циклу завжди реалізується по входу 1. При цьому змінна циклу "і" набуває початкового значення циклу n_п. Далі відбувається порівняння змінної циклу "і" по відношенню до параметру кінця циклу n_к: . Якщо така нерівність істинна, відбувається перехід по каналу 2, будуть виконуватися блоки тіла циклу, до "і" буде добавлений крок переадресаціїк_р і відбудеться повернення в блок по каналу 3 для подальшої перевірки . Коли ж нерівністьстає хибною (і стане більшим) здійснюється закінчення циклу з виходом по каналу 4.

Дії блоку “Підготовчі операції” залежать від типу задачі і для задач обробок елементів одновимірних масивів наведені в таблиці 6.

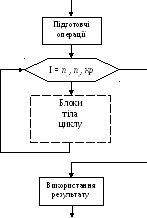
1

3 4

2

Рисунок 5 – Типова блок-схема циклу з визначеною кількістю повторень

Таблиця 6

Тип задачі	Підготовчі операції	Дії
1	Знаходження суми визначених елементів	S=0
2	Знаходження добутку визначених елементів	D=1
3	Підрахунок кількості визначених елементів	K=0
4	Знаходження визначеного елемента	t=a1
5	Знаходження рівня визначеного елемента	t=a1; r=1

Під визначеними елементами масиву розуміють найбільший, додатній, від’ємний, більший числа Z, найменший по модулю тощо.

Масиви в Pascal описуються по зразку:

A: array [n_п..n_к] of <типи даних масиву>;

На рисунку 6 приведений приклад знаходження в одновимірному масиві рівня найбільшого по модулю елемента. Вважається, що масив уже знаходиться в оперативній пам’яті комп’ютера.

Елементи двовимірного масиву (числової таблиці) реалізуються з допомогою вкладених циклів. На внутрішньому циклі виконується одна із задач обробки елементів одновимірного масиву (рядка або стовпця), а на зовнішньому відбувається перехід від одного стовпця (рядка) до іншого.

Всі задачі обробки матриць реалізуються по одній із двох фрагментів типових блок-схем (рисунок 7-а чи рисунок 7-б). Блок-схема 7-а, застосовується в тому випадку, якщо потрібно знайти результат, що характеризує елементи всієї матриці (наприклад, найбільший елемент матриці, сума від’ємних елементів матриці, кількість елементів більших числа Z в матриці і т.д.). Фрагмент блок-схеми 7-б здійснює одержання показника для рядків або стовпців матриці (наприклад, кількість елементів менших числа Z в кожному стовпці матриці).

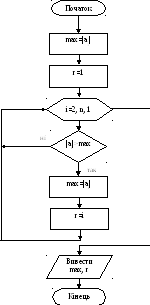
Рисунок 6 – Приклад блок-схеми циклічного процесу з визначеною кількістю повторень

Якщо вибір індексу для зовнішнього циклу для фрагмента 7а) не впливає на результат роботи алгоритму, для фрагмента 7б) таким індексом (рядків чи стовпців) обов’язково повинен бути той, для якого розв’язується задача. Наприклад, для задачі підрахунку суми додатніх елементів в кожному стовпці матриці індексом зовнішнього циклу повинен бути індекс стовпців.

Таким чином, при розробці алгоритму обробки елементів двовимірного масиву рекомендується притримуватися такої інструкції:

1. визначити, до якого типу (7-а чи 7-б) відноситься задача;

2. якщо задача відноситься до типу рисунка 7-б, вибрати потрібний індекс зовнішнього циклу блок-схеми;

3. визначити, до якого типу (таблиця 6) відноситься внутрішній цикл задачі і відповідно до нього вибрати підготовчі операції;

4. по даним попереднього аналізу побудувати блок-схему алгоритму.

Матриця на мові Pascal оголошується по зразку:

M: array [n_п..n_к, m_п..m_к] of <тип>;

де n_і – індекси рядків, m_і – індекси стовпців.