1.3. Класичне визначення ймовірності

Ймовірність - одне з основних понять теорії ймовірностей. Існує кілька визначень цього поняття. Приведемо визначення, що називають класичним. Далі вкажемо слабкі сторони цього визначення і приведемо інші визначення, що дозволяють перебороти недоліки класичного визначення.

Розглянемо приклад. Нехай в урні міститься 6 однакових, ретельно перемішаних куль, причому 2 з них - червоні, 3 - сині і 1 - біла. Очевидно, можливість вийняти навмання з урни кольорову (тобто червону чи синю) кулю більша, ніж можливість витягти білу кулю. Чи можна охарактеризувати цю можливість числом? Виявляється, можна. Це число і називають ймовірністю події (появи кольорової кулі).

Таким чином, ймовірність є число, що характеризує ступінь можливості появи події.

Поставимо перед собою завдання дати кількісну оцінку можливості того, що узята навмання куля кольорова. Появу кольорової кулі будемо розглядати як подію А. Кожний з можливих результатів випробування (випробування полягає у діставанні кулі з урни) назвемо елементарним результатом (елементарною подією). Елементарні події позначимо через і т.д. У нашому прикладі можливі наступні 6 елементарних результатів:- з’явилася біла куля;- з’явилася червона куля;- з’явилася синя куля. Легко бачити, що ці результати утворять повну групу попарно несумісних подій (обов’язково з’явиться тільки одна куля) і вони рівноможливі (кулю виймають навмання, кулі однакові і ретельно перемішані).

Ті елементарні результати, у яких подія, що нас цікавить, настає, назвемо такими, що сприяють цій події. У нашому прикладі сприяють події А (появі кольорової кулі) наступні 5 результатів: .

Таким чином, подія А спостерігається, якщо в випробуванні настає один, байдуже який, з елементарних результатів, що сприяють А; у нашому прикладі А спостерігається, якщо наступить абоабоабоабо. У цьому розумінні подія А підрозділяється на кілька елементарних подій (); елементарна ж подія не підрозділяється на інші події. У цьому полягає розходження між подієюА і елементарною подією (елементарним результатом).

Відношення числа сприятливих події А елементарних результатів до їх загального числа називають ймовірністю події А і позначають через Р (А). У розглянутому прикладі усього елементарних результатів 6; з них 5 сприяють події А. Отже ймовірність того, що взята куля виявиться кольоровою, дорівнює Р (А) = 5/6. Це число і дає ту кількісну оцінку ступеня можливості появи кольорової кулі, що ми хотіли знайти. Дамо тепер визначення ймовірності.

Ймовірністю події А називають відношення числа сприятливих цій події результатів до загального числа всіх рівноможливих несумісних елементарних результатів, що утворюють повну групу.

Отже, ймовірність події А визначається формулою

де m - число елементарних результатів, що сприяють події А; n - число всіх можливих елементарних результатів випробування.

Тут передбачається, що елементарні результати несумісні, рівноможливі й утворюють повну групу. З визначення ймовірності випливають наступні її властивості:

Властивість 1. Ймовірність достовірної події дорівнює одиниці.

Дійсно, якщо подія достовірна, то кожен елементарний результат випробування сприяє події. У цьому випадку m=n, отже,

Властивість 2. Ймовірність неможливої події дорівнює нулю.

Дійсно, якщо подія неможлива, то жоден з елементарних результатів іспиту не сприяє події. У цьому випадку m = 0, отже,

Властивість 3. Ймовірність випадкової події є позитивне число, укладене між нулем і одиницею.

Дійсно, випадковій події сприяє лише частина з загального числа елементарних результатів випробування. У цьому випадку , отже виходить, що, отже,

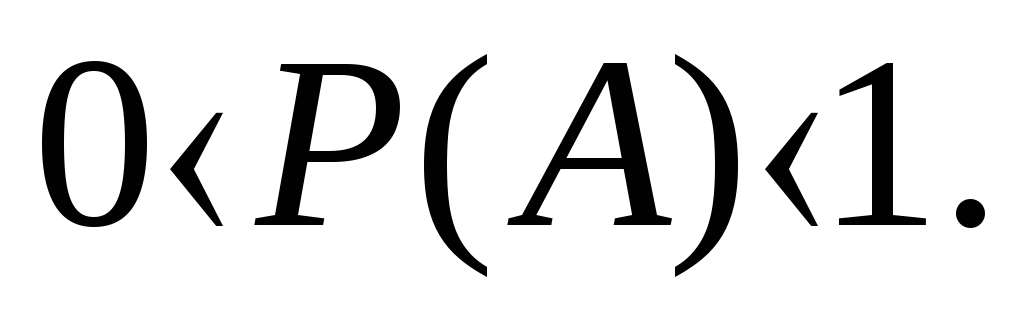
Отже, ймовірність будь-якої події задовольняє подвійній нерівності

Далі будуть приведені теореми, що дозволяють за заданими ймовірностями одних подій знаходити ймовірності інших подій.

Зауваження. Сучасні строгі курси теорії ймовірностей побудовані на теоретико-множинній основі. Обмежимося викладенням мовою теорії множин тих понять, що розглянуті вище.

Нехай у результаті іспиту настає одна і тільки одна з подій ...Подіїназиваютьелементарними подіями (елементарними результатами). Уже звідси випливає, що елементарні події попарно несумісні. Безліч усіх елементарних подій які можуть з’явитися у випробуванні, називають простором елементарних подій , а самі елементарні події -точками простору .

Подію А ототожнюють з підмножиною (простору ), елементи якого є елементарні результати, що сприяють подіїА; подія В є підмножина , елементами якої є результати, що сприяютьВ, і т.д. Таким чином, множина усіх подій, що можуть наступити у випробуванні, є безліч усіх підмножин . Саменастає при будь-якому результаті випробування, тому- достовірна подія; порожня підмножина простору- неможлива подія (вона не настає ні при якому результаті випробування).

Відмітимо, що елементарні події виділяються з числа всіх подій тим, що кожна з них містить тільки один елемент .

Кожному елементарному результату ставлять у відповідність позитивне число- ймовірність цього результату, причому.

За визначенням, ймовірність подіїдорівнює сумі ймовірностей елементарних результатів, що сприяють події. Звідси легко отримати, що ймовірність достовірної події дорівнює одиниці, неможливої – нулю, довільної – знаходиться між нулем та одиницею.

Розглянемо важливий частковий випадок, коли всі результати рівноможливі. Число результатів дорівнює , сума ймовірностей всіх результатів дорівнює одиниці, значить ймовірність кожного результату дорівнює. Нехай подіїсприяєрезультатів. Ймовірність подіїдорівнює сумі ймовірностей результатів, що сприяють:

P(A)=1/n+1/n+…1/n.

З огляду на те, що число складових дорівнює , маємо

P(A)=m/n.

Отримано класичне визначення ймовірності.

Побудова логічно повноцінної теорії ймовірностей ґрунтується на аксіоматичному визначенні випадкової події і її ймовірності. У системі аксіом, запропонованій О.М. Колмогоровим, невизначуваними поняттями є елементарна подія і ймовірність. Приведемо аксіоми, що визначають ймовірність:

1. Кожній події А поставлено у відповідність невід’ємне дійсне число Р(А). Це число називається ймовірністю події А.

2. Ймовірність достовірної події дорівнює одиниці:

P () =1.

3. Ймовірність настання хоча б однієї із попарно несумісних подій дорівнює сумі ймовірностей цих подій.

Виходячи з цих аксіом, властивості ймовірностей і залежності між ними виводять в якості теорем.