4.3. Інтегральна теорема Лапласа

Знову припустимо, що проводиться n випробувань, в кожному з яких ймовірність появи події А постійна і рівна р (0<р<1). Як обчислити ймовірність того, що подія А з’явиться в n випробуваннях не менш k₁і не більше k₂разів (скорочено будемо говорити „від k₁до k₂разів”)? На це питання відповідає інтегральна теорема Лапласа, яка приводиться нижче без доведення.

Теорема.Якщо ймовірність р настання події А в кожному випробуванні постійна і відмінна від нуля і одиниці, то ймовірністьтого, що подія А з’явиться в n випробуваннях від k₁до k₂разів, приблизно дорівнює визначеному інтегралу

, (*)

де і.

При розв’язанні задач, що вимагають застосування інтегральної теореми Лапласа, користуються спеціальними таблицями, оскільки невизначений інтеграл не виражається через елементарні функції. Таблиця для інтегралаприводиться в довідниках. В таблиці даються значення функціїдля позитивних значень х і для х=0; для x<0 користуються тією ж таблицею (функціянепарна, тобто). В таблиці приведені значенні інтеграла лише до х=5, так як дляможна прийняти. Функціючасто називаютьфункцією Лапласа.

Для того щоб можна було користуватися таблицею функції Лапласа, перетворимо співвідношення (*) так:

.

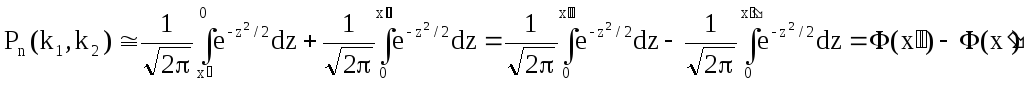Отже, ймовірність того, що подія А з’явиться в n незалежних випробуваннях від k₁до k₂разів,

,

де і.

Зауваження.Позначимо через m число появ події A при n незалежних випробуваннях, в кожному з яких ймовірність настання події А постійна і рівна р. Якщо число m змінюється від k₁до k₂, то вираззмінюється віддо. Отже, інтегральну теорему Лапласа можна записати і так:

.

Ця форма запису використовується нижче.

4.4. Ймовірність відхилення відносної частоти від постійної ймовірності в незалежних випробуваннях

Знову будемо вважати, що проводиться n незалежних випробувань, в кожному з яких ймовірність появи події А постійна і рівна р (0<р<1). Поставимо перед собою завдання знайти ймовірність того, що відхилення відносної частоти від постійної ймовірності р за абсолютною величиною не перевищує заданого числа. Іншими словами, знайдемо ймовірність здійснення нерівності

. (*)

Цю ймовірність будемо позначати так: Р().Замінимо нерівність (*) їй рівносильними:

або.

Перемноживши ці нерівності на додатній множник , отримаємо нерівності, рівносильні початковій:

.

Скористаємося інтегральною теоремою Лапласа у формі, указаній в зауваженні (див. 4.3). Поклавши і, маємо

.

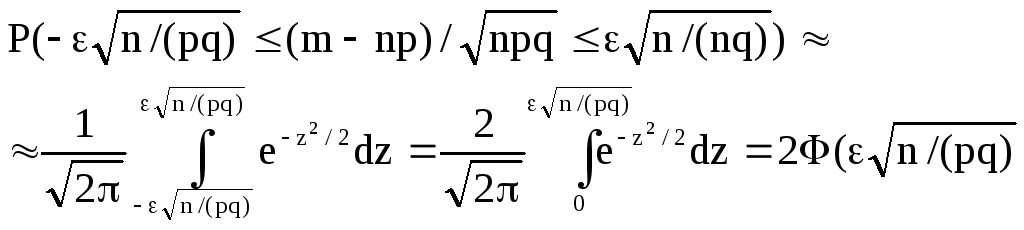Нарешті, замінивши нерівності, що знаходяться в дужках, рівносильною їм початковою нерівністю, остаточно отримаємо

.

Отже, ймовірність здійснення нерівності приблизно дорівнює значенню подвоєної функції Лапласапри.

Запитання для самоперевірки:

1. Які випробування називають незалежними щодо події А?

2. Поясніть поняття «складна подія».

3. Виведіть формулу Бернуллі.

4. Сформулюйте локальну теорему Лапласа (Муавра – Лапласа).

5. При яких умовах застосовується локальна теорема Лапласа?

6. Сформулюйте інтегральну теорему Лапласа.

7. Як на практиці обчислити ймовірність того, що подія А з’явиться від 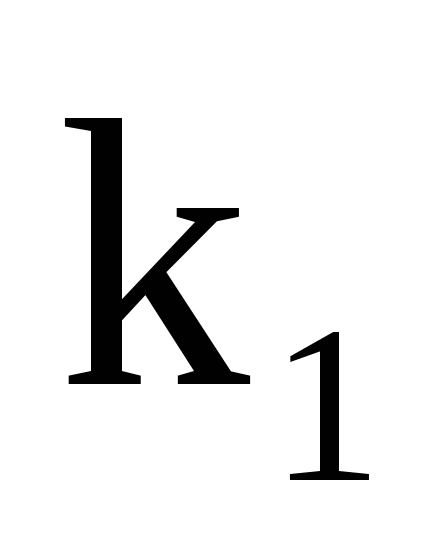до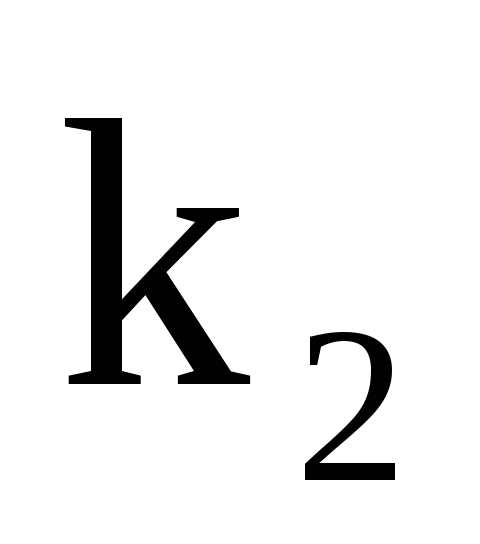разів в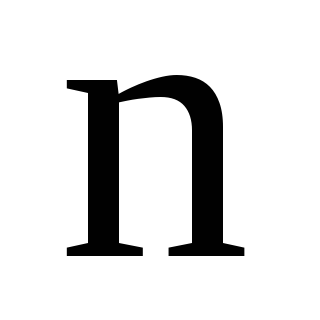незалежних випробувань, якщо ймовірність її появи в кожному випробуванні постійна і відмінна від нуля и одиниці?

8. Як обчислити ймовірність відхилення відносної частоти від постійної ймовірності в незалежних випробуваннях?