6.5. Раскрытие неопределенностей. Правило Лопиталя

6.6. Основные свойства дифференцируемых функций

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный экономический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Высшая математика. Практикум, часть 1.pdf

Скачиваний:

193

Добавлен:

20.02.2016

Размер:

2.91 Mб

Скачать

☆

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 2829 / 3329 30 31 32 33 > Следующая >>>

Пусть функции f (x) и g(x) определены на интервале (a,b) и имеют

конечные производные f (x)		и g (x) в этом промежутке, за исключением,
′		′	x ≠ a . Если обе функции
быть может, точки x = a ,	причем g (x) ≠ 0 при
		′

бесконечно малые или бесконечно большие при x → a , то говорят, что частное f (x)g(x) при x → a представляет неопределенность вида 00 или ∞∞.

	Первое		правило		Лопиталя	[0/0].	Если	lim	f (x) = lim g( x) = 0,	то
								x→a	x→a
lim	f (x)	= lim	f ′(x)	, когда последний предел существует.
lim		= lim	′	, когда последний предел существует.
x→a g(x)		x→a g (x)
	Второе		правило		Лопиталя	[∞/∞].	Если	lim f (x) = lim g( x) = ∞,		то
								x→a	x→a
lim	f (x)	= lim	f ′(x)	, когда последний предел существует.
lim		= lim	′	, когда последний предел существует.
x→a g(x)		x→a g (x)
	Неопределенности				вида ∞ −∞, 0 ∞ и			00,	∞0, 1∞ сводятся	к

неопределенностям вида 0/0 и ∞/∞ путем алгебраических преобразований и логарифмирования:

• В случае неопределенности вида 0 ∞ или ∞ −∞ следует алгебраически преобразовать данную функцию так, чтобы привести ее к неопределенности вида 0/0 или ∞/∞ и далее воспользоваться правилом Лопиталя.

• В случае	неопределенности				вида 00 или ∞0, или 1∞ следует
прологарифмировать данную функцию и найти предел ее логарифма.
Если частное	f (x) g (x)		в точке х=a также есть неопределенность вида
	′	′	f (x) и		g (x) удовлетворяют соответствующим
0/0 или ∞/∞ и производные
			′		′
условиям, то следует перейти к отношению вторых производных и т. д.
Пример 6.40. Найти предел lim				x2 + ln x −1		.
					ex −e
			x→1
Решение.	Числитель и знаменатель стремятся к нулю при x →1, а по-

тому имеем неопределенность вида 0/0. Воспользуемся правилом Лопиталя, т.е. рассмотрим предел отношения производных заданных функций:

lim	x2	+ ln x −1	= lim	2 x +1 x	=	3	.
		ex −e		ex		e
x→1			x→1

221

Пример 6.41. Найти lim ln x .

x→ +∞ x

Решение. Раскрываемнеопределенностьвида∞/∞ поправилуЛопиталя:

lim

1/ x

lim

= 0.

x→ +∞

x→ +∞1/ (2 x)

x→ +∞

Пример 6.42. Найти предел lim

x −sinx

x→0

Решение.

Неопределенность

вида

0/0.

Имеем lim

x −sinx

1−cos x

= lim sinx =

x→0

= lim

1 – правило Лопиталя применено трижды.

x→0

3x2

x→0

Пример 6.43. Найти предел функции y = 1x − ex1−1 при x → 0.

Решение. Имеем неопределенность вида ∞ −∞. Сначала преобразуем ее к неопределенности вида 0/0, для чего достаточно привести дроби к общему знаменателю. К полученному выражению два раза применим правило Лопиталя. Записывая последовательно все вычисления, будем иметь

lim(

−

) =

lim

ex −1− x

= lim

(ex −1− x)′

= lim

ex −1

x(ex −1)

(x(ex −1))′

xex −1+ ex

x→0

= lim

(ex −1)′

= lim

= 1 .

(xex −1+ ex )′

xex + ex + ex

x→0

Пример 6.44. Вычислить lim (ex + x)1x .

x→0

Решение. Неопределенность вида 1∞. Пусть A – искомый предел.

	1		ln(ex + x)			ex +1
Тогда ln A =	( ln(ex + x ))=	lim		=	lim		= 2,	A = e2 .

lim	x		x			ex + x
x→0		x→0			x→0

222

Задачи для самостоятельного решения

6.75. Вычислить пределы, используя правило Лопиталя:

1)	lim	x3		−3x2 + 7x −5				;
				+ 2x2 −9x + 6
	x→1 x3
3)	lim		x4 + x3 −3x2 −5x − 2						;
				x4 + 2x3			− 2x −1
	x→−1
5)	lim	ex −e−x				;
			sin 4x
	x→0
7)	lim ln(cos x)					;
	x→0			x2
9)	lim	e3x −1			;
			sin x
	x→0
11)	lim x3 ln x ;
	x→+0
13)	lim			xln2 x ;
	x→+0

2)	lim		2x −3x				;
2)	lim		x2 +3x				;
	x→0		x2 +3x
4)	lim ln(1+ x) − x							;
	x→0					x2
6)	lim		sin15x				;
	x→π		sin9x
8)	lim			cos7x ;
	x→π	/2		cos5x
10)	lim			sin 7x −7sin x					;
10)	lim								;
	x→0					x2
				3		−1
12)	lim			3	x	−1	;

					x −1
	x→1				x −1
14)	lim			sin xln x .
	x→+0

6.76. Найти пределы функций, пользуясь правилом Лопиталя:

1)	lim tg 2x −ln(1+ 2x)					;
	x→0		x2
3)	lim		tg x − x	;
3)	lim			;
	x→0 x −sin x
5)	lim	xcos x −sin x			;
5)	lim				;
	x→0		x3
7) lim(sin x)x ;
	x→0
9)	lim (π − 2x) tg x ;
	x→π
	2

11) lim(sin x)x ;

x→0

2) lim	ex −e−x − 2x	;
	x −sin x
x→0

4) lim xx ;

x→+0

6) lim 1−cos7x ; x→0 xsin 7x

8) lim (sin 2x)cos x ;

x→π2

10) lim x1+ln x ;

x→0

12) lim (tg x)2x−π .

x→π2

223

6.104. Написать формулу Маклорена n-го порядка для функции y = xex .

6.105. Написать формулу Тейлора n-го порядка для функции y =

при a = 4 .

при a = 4 .

6.106. Написать формулу Маклорена 2n-го порядка для функции

6.106. Написать формулу Маклорена 2n-го порядка для функции

Теорема Ферма. Пусть функция f (x) определена на интервале (a, b и

в некоторой точке x0		этого интервала принимает наибольшее или
наименьшее значение.	Тогда возможны только два случая: 1) производная
f ′(x0 ) не существует;		2) f ′(x0 ) = 0.

Геометрический смысл этого утверждения – касательная к графику в точке локального экстремума параллельна оси Ox или график функции имеет излом в точке x0 (рис. 6.5).

Рис. 6.5

Теорема Ролля. Пусть функция f (x) удовлетворяет условиям:

1)непрерывна на отрезке [a,b];

2)имеет производную на интервале (a,b) ;

3)на концах интервала принимает равные значения: f (a) = f (b) . Тогда существует хотя бы одна точка c (a,b), такая, что f ′(c) = 0 .

Геометрический смысл теоремы Ролля заключается в том, что на графике функции,удовлетворяющейусловиютеоремы,обязательносуществуетточка(по крайнеймере,одна),вкоторой касательнаякграфикупараллельнаоси Ox .

224

Теорема Лагранжа. Пусть функция y = f (x) непрерывна на отрезке [a,b] и имеет производную в каждой точке интервала (a,b) . Тогда существует такая точка c (a,b), что

f (b) − f (a) = f ′(c)(b − a).

Часто этот факт упоминается как формула конечных приращений Лагранжа f (x + ∆x) − f (x) = f ′(x +θ ∆x) ∆x, 0 <θ <1.

Физическая интерпретация теоремы Лагранжа состоит в том, что существует такой момент времени х = с, в который мгновенная скорость равна средней скорости на временном отрезке [a, b].

Геометрический смысл – на интервале (a, b) найдется такая точка c, что касательная к графику в точке C(c, f (c)) параллельнасекущейАВ(рис.6.6).

Напомним, что формулой бесконечно малых
приращений называют приближенное равенство
f (x + ∆x) ≈ f (x) + f (x)∆x при малых ∆x .
′

Теорема Коши. Пусть функции f (x) и g(x) непрерывны на отрезке
[a,b] и имеют производные в каждой			точке интервала (a,b) , причем
g (x) ≠ 0 для всех x (a,b). Тогда существует такая точка c (a,b), что
′
	f (b) − f (a)		′
		=	f (c)
			′
	g(b) − g(a)		g (c)

(обобщенная формула конечных приращений Коши).

Формула Тейлора. Многочлен степени не выше п

T	(x) =T (x; f ) =	f (a) +	f ′(a)	(x − a) +	f ′′(a)	(x − a)2 +... +	f (n) (a)	(x − a)n

n	n	1!			2!		n!

называется многочленом Тейлора функции					f (x)	в окрестности точки a .

Если функция f (x) – многочлен n-й степени, то Tn (x) – ее точное разложение по степеням (x − a) , т.е. Tn (x; f ) = f (x) при любом x.

225

Если функция			f (x) имеет производные				до (n +1) -го		порядка
включительно в интервале (x0 −ε, x0 +ε), ε > 0 , то для всех								x	из этого
интервала справедлива формула Тейлора n-го порядка
				f (x) =Tn (x) + Rn+1(x) ,
где R	(x; f ) = R	(x) =		f (n+1) (ξ)	(x − a)n+1,	ξ (a −ε,	a +ε) – остаточный
где R	(x; f ) = R	(x) =			(x − a)n+1,	ξ (a −ε,	a +ε) – остаточный
n+1	n+1			(n +1)!
				(n +1)!
член в форме Лагранжа. Величина Rn+1(x)						– бесконечно малая порядка n +1
относительно x − a			в окрестноститочкиa .

При а = 0 многочлен Тейлора называется также многочленом Маклорена.

Многочлен Тейлора-Маклорена служит достаточно хорошим средством приближенного представления функции и широко применяется в приближенных вычислениях с заданной точностью, оцениваемой абсолютной величиной остаточного члена Rn+1(x) .

МногочленыМаклорснадлянекоторыхизэлементарныхфункцийимеютвид:

1) (1

+ x)

=1+ nx

n(n −1)

n(n −1)(n − 2)

+ nx

n−1

2 3

Эта формула называется биномом Ньютона;

2) T

(x;ex ) =1+ x +

+ +

, R

(x) =

eξ

(x − a)n+1;

n+1

(n +1)!

T (x;sinx) = x −

−

+ + (−1)n−1

x2n−1

(2n −1)!

(x) = sin(ξ +

(n +1))

xn+1

x ;

n+1

(n +1)!

(x; cos x) =1−

−

+ + (−1)n

x2n

(2n)!

(x) = cos(ξ +

(n +1))

xn+1

x ;

n+1

(n +1)!

α(α −1)

α(α −1)(α − 2)

5) Tn (x; (1

+x) ) =

1+αx +

α(α −1) (α − n +1)

xn ,

(x)

α(α −1) (α − n)

(1+ξ)α−n xn+1 , | x |<1;

n+1

(n +1)!

xn+1

(x;ln(1+ x)) = x −

+... +

(−1)n−1 xn ,

| R

(x) | =

, x (−1;1).

n+1

(1+ξ)n+1(n +1)

226

Пример 6.45. Выполняется ли теорема Ролля	для	функции
f (x) = x2 −6x +100 , если а= 1, b=5? При каком значении c?
Решение. Так как функция f (x) непрерывна и дифференцируема при
всех значениях х и ее значения на концах отрезка [1, 5] равны:	f (1) = f	=(5) ,

то теорема Ролля на этом отрезке выполняется. Значение c определяем из уравнения f ′(c) = 2c −6 = 0 , т.е. c = 3.

Пример 6.46. Функция f (x) = 3(x −8)2 непрерывна на отрезке [0, 16], на концах которого она принимает равные значения: f (0) = f (16) = 4. Однако ее

(33

) не обращается в нуль ни в одной точке

производная

f (x) = 2

(x −8)2

интервала (0, 16). Противоречит ли это теореме Ролля?

Решение. Нет, так как в точке x =8 интервала ]0, 16[ производная не

существует, и условия теоремы Ролля нарушены.

Пример

6.47.

Показать,

что

производная

многочлена

f (x) = x3 − x2 − x +1 имеет действительный корень в интервале ]–1, 1[.

Решение. Найдем корни данного многочлена:

f (x) = x3 − x2 − x +1 = 0

или (x −1)2 (x +1) = 0, т.е.

= x =1,

x = −1.

Так как

f (−1) = f (1) = 0 ,

то по

теореме Ролля

f (x)

интервале

] −1, 1[.

Найдем

корни

имеет корень

′

производной

′

− 2x −1 = 0 ,

т.е.

x1 = −1 3, x2 =1. Таким образом,

(x) = 3x

между корнями функции −1 и 1 содержится корень производной, равный

−1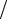3 .

Пример 6.48. На дуге AB кривой y = 2x - x2 найти точку М, в которой касательная параллельна хорде АВ, если A(1; 1) и B(3; –3).

Решение. Функция y = 2x − x2 непрерывна и дифференцируема при всех значениях х. По теореме Лагранжа между двумя значениями a =1 и b = 3

существует	значение	y		x = c ,	удовлетворяющее	равенству
y(b) − y(a) = (b − a)y (c), где		y	′	= 2 − 2x .	Подставив значения a	и b, получим
	′		′
y(3) − y(1) = (3 −1)y '(c); (2 3 −32 ) −(2 1−12 ) = (3 −1) (2 − 2c); −4 = 4 (1−c) .
Откуда c = 2,	y(2) = 0 . Таким образом, точка Мимеет координаты (2; 0).

Пример 6.49. Вычислить с точностью до 10−3 значение sin 20°

227

Решение. Имеем sin 20 = sin

π 3

−

− . Число

членов в этой части следует брать из условия

<10−3 . Для n = 3 имеем

n+1

оценку

sin(ξ

+ π (3 +1)) π

n+1

≤

π 4

< 0,00063 <10−3

n+1

(3 +1)!

π 3

Следовательно, sin 20 ≈

−

≈ 0,342 .

Пример

6.50.

Многочлен

y = x6 − 2x2 +3x +5 разложить по целым

положительным степеням бинома х – 2.

Решение. Находим все нетривиальные производные: y′ = 3x2 − 4x +3,

y′′ = 6x − 4 ,

y′′′

= 6,

yIV = 0 .

Вычисляем значения функции и этих производных при x = 2

y(2) =11,

′

′′

′′′

y (2) = 2,

y (2) =8,

(2) = 6.

Согласно формуле Тейлора записываем

y =T (x) =11+ 7(x − 2) + 4(x − 2)2 + (x − 2)3 .

Пример 6.51. Написать многочлен Тейлора третьей степени с центром в

точке x = 3 для функции f (x) =

1+ x

Решение. Согласно формуле Тейлора имеем

T (x) = c

+ c (x −3) + c (x −3)2 + c (x −3)3 ,

где

f (k ) (3)

Найдем производные

f ′(x) =

f ′′(x) =

−1

f ′′′(x)

1+ x

(1+ x)3

(1+ x)5

′

′′

−1

′′′

(3)

f (3)

Вычисляем ck : c0 = f (3),

c1 = f (3) =

, c2

, c3

512

В итоге получаем T (x) = 2 + 1 (x −3) −

(x −3)2 +

(x −3)3 .

512

228

Задачи для самостоятельного решения

6.77. Проверить справедливость теоремы Ролля для функции f (x) = x3 + 4x2 −7x −10 на отрезке [–1, 2].

6.78. Проверить справедливость теоремы Ролля для функции y = ln sin x на отрезке [π / 6, 5π/ 6] .

6.79.Проверить справедливость теоремы Ролля для функции y = 4sin x на отрезке [0, π .

6.80.Проверить справедливость теоремы Ролля для функции y = 3x2 −3x + 2 на отрезке [1, 2].

6.81. Функция y = (2 − x4 )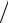x2 принимает равные значения на концах отрезка [–1, 1]. Убедиться в том, что производная от этой функции нигде на отрезке [– 1,1]внульнеобращается,иобъяснитьтакоеуклонениеоттеоремыРолля.

6.82. Функция y =| x | принимает равные значения на концах отрезка [−a, a]. Убедиться в том, что производная от этой функции нигде на отрезке [−а, а] в нульнеобращается,иобъяснитьтакоеуклонениеоттеоремыРолля.

6.83. В какой точке дуги АВ кривой y = x3 −3x касательная параллельна хорде

	АВ, если A(0; 0), B(3; 18)?
6.84.	Написать формулу Лагранжа для функции y = sin 3x на отрезке [x1, x2 ].
6.85. Написать формулу Лагранжа для функции y = x(1−ln x) на отрезке [a,b].
6.86.	Написать формулу			Лагранжа для		функции y = arcsin 2x на отрезке
	[x0, x0 + ∆x].
6.87.	Проверить справедливость теоремы Лагранжа для функции						y = xn	на
	отрезке [0, a для n > 0, a > .
6.88.	Проверить справедливость теоремы Лагранжа для функции						y = ln x	на
	отрезке [1, е].
6.89. Доказать с помощью формулы Лагранжа двойное неравенство
				a −b	≤ ln a ≤ a −b , 0 < b ≤ a .
				a	b	b
6.90. Доказать с помощью формулы Лагранжа неравенства
		α − β		α − β
			≤ tgα − tg β ≤		при условии 0 < β ≤α <π 2.
		cos2 β	≤ tgα − tg β ≤	cos2 α	при условии 0 < β ≤α <π 2.

229

6.91. Доказать с помощью формулы Лагранжа справедливость при а>b

неравенств

nbn−1(a −b) < an −bn < nan−1(a −b),

если n >1 и неравенств

противоположного смысла, если n <1.

6.92.

Используя

формулу

f (x0 + ∆x) ≈ f (x0 ) + f

′(x0

+ ∆x) ∆x ,

вычислить

приближенные значения данных выражений. Сравнить результат с

табличным: а) arcsin 0,54;

б)

lg11;

в) lg 61.

6.93. Написать формулу Коши для функций

f (x) = sin x и g(x) = ln x на отрезке

[a, b], 0<a<b.

6.94.

Написать формулу Коши для функций

f (x) = e2x и g(x) = e1+x

на отрезке

[a, b].

6.95. Проверить

справедливость

формулы

Коши

для

функций

f (x) = x3 и

g(x) = x2 +1 на отрезке [1, 2].

6.96. Проверить справедливость формулы Коши для функций f (x) = sin x и

g(x) = x + cos x на отрезке [0, π

/ .

6.97.

Доказать,

что

если

на

отрезке [a,b] имеет

место соотношение

f (x) ≥ g (x)

g (x)

не обращается в нуль, то справедливо также

′

соотношение

∆f (x)

≥

∆g(x)

где

∆f (x) = f (x + ∆x) − f (x) ,

∆g(x) = g(x + ∆x) − g(x) , а x и x + ∆x – произвольные точки отрезка [a,b].

6.98.Разложить многочлен x4 −5x3 + x2 −3x + 4 по степеням двучлена x − 4 , пользуясь формулой Тейлора.

6.99.	Разложить	многочлен		x3 +3x2 − 2x + 4 по степеням двучлена x +1,
	пользуясь формулой Тейлора.
6.100. Разложить многочлен x10 −3x5 +1 по степеням двучлена x −1.
6.101.	Функцию	f (x) = (x2 −3x +1)3 разложить по				степеням		x ,	пользуясь
6.102.	формулой Тейлора.					что	f (2) = −1, f (2) = 0,
6.102.	f (x) – многочлен четвертой степени. Зная,					что	f (2) = −1, f (2) = 0,
									′
	′′	′′′	f	iv	(2) = 24, вычислить f (−1) ,		′	f	′′
	f (2) = 2, f	(2) = −12,	f		(2) = 24, вычислить f (−1) ,		f (0),	f	(1).

230

6.103. Написать формулу Тейлора n-го порядка для функции y = 1x при a = −1.

6.107. Написать формулу Тейлора2n-гопорядкадляфункции y = x3 ln x при a =1.

6.108. Написать формулу Маклорена 2n-го порядка для функции y = sin2 x .

6.109. Написать формулу Тейлора 3-го порядка для функции y = x x−1 при a = 2 и

построитьграфикиданнойфункциииеемногочленаТейлора3-йстепени. 6.110. Написать формулу Маклорена 2-го порядка для функции y = tg x и построить

графикиданнойфункциииеемногочленаМаклорена2-йстепени.

6.111. Написать формулу Маклорена 3-го порядка для функции								y = arcsin x и
	построитьграфикиданнойфункциииеемногочленаМаклорена3-йстепени.
6.112. Написать формулу Тейлора 3-го порядка для функции y =						1			при	a =1 и

							x
							x
	построитьграфикиданнойфункциииеемногочленаТейлора3-йстепени.
6.113.	Для	функции	f (x) = x10 −3x6 + x2 + 2	найти	три	первых				члена
	разложения по формуле Тейлора при a =1. Найти приближенно f (1,03) .
6.114.	Для	функции	f (x) = x8 − 2x7 +5x4 − x +3	найти	три	первых				члена
	разложения по формуле Тейлора при a = 2 . Найти приближенно f (2,02) и
	f (1,97) .

6.115. Проверить, что при вычислении значения функции ex при 0 < x ≤ 0,5 по

приближенной формуле ex ≈1+ x +	x2	+	x3	допускаемая погрешность

2		6

меньше 0,01. Пользуясь этим, найти приближенно 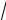e .

231

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 2829 / 3329 30 31 32 33 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.02.201638.4 Кб21Высшая матем, программа 1 семестр.doc
#
20.02.20161.66 Mб93Высшая математика - 2.Уч.-практ.пособие.pdf
#
20.02.20161.62 Mб60Высшая математика 3 семестр часть 1.doc
#
20.02.20163.1 Mб102Высшая математика 3 семестр часть 2.doc
#
20.02.2016450.37 Кб73высшая математика 3семестр.pdf
#
20.02.20162.91 Mб193Высшая математика. Практикум, часть 1.pdf
#
20.02.20161.12 Mб60Высшая математика. Ряды. Уч-метод. пособие.pdf
#
20.02.20162.82 Mб243Высшая математика.Практикум.pdf
#
20.02.20161.59 Mб126Высшая_математика__2_семестр_ (1).pdf
#
20.02.201636.86 Кб14высшка 3 семестр примерный перечень вопросов.doc
#
20.02.201619.69 Кб24Выш мат.docx