Tom_2

Найти среднее значение выборки, дисперсию и стандартное отклонение.

Решение. Вначале найдем среднее арифметическое по исходным данным валового сбора зерновых в хозяйствах:

Теперь легко найти, что выборочная дисперсия

D = 53400 = 6675 . 8

Извлекая из дисперсии корень, получим величину выборочного стандартного отклонения σ€ » 82 ц. □

Таким образом, можем заключить, что степень разброса в данной выборочной совокупности невелика.

Для сравнения средних стандартных отклонений различных выборок из одной генеральной совокупности вычисляют коэффициент вариации, который определяется по формуле

v = σx€ ×100 % ,

434

т.е. коэффициент вариации равен процентному отношению выборочного стандартного отклонения к среднему выборочному.

20. Мода и медиана. Наряду со средним выборочным в качестве статистических характеристик вариационных рядов рассматриваются структурные средние – мода и медиана.

Мода m0 выборки представляет собой значение варианты,

повторяющееся с наибольшей частотой. Если две или более несмежных вариант имеют разные наибольшие частоты, то вариационный ряд называют бимодальным или полимодальным. В этом случае можно говорить о неоднородности выборки.

Медианой me называют значение параметра, относительно

которого статистическая совокупность делится на две равные по объему части, причем в одной из них содержатся члены, у которых значения параметра не больше me , а в другой – члены со значениями

параметра не меньше me .

Если сумма абсолютных частот n дискретного вариационного ряда нечетная, то медиана me определяется по формуле

Пример 2. Рабочие бригады из 11 человек имеют следующие тарифные разряды: 9, 5, 9, 6, 6, 8, 7, 6, 7, 8, 6. Найти моду и медиану в ы б о р к и .

Решение. Проведем упорядочивание статистического ряда по возрастанию: 5, 6, 6, 6, 6, 7, 7, 8, 8, 9, 9.

Очевидно, m0 = 6 . Мода отражает наиболее распространенную

варианту рассматриваемого признака. В данном случае это будет рабочий шестого разряда. Можно заметить, что моду легко определять, если воспользоваться полигоном частот.

Легко найти также медиану, me = 7 . Именно рабочий седьмого разряда находится на середине статистического ряда. □

Вотличие от дискретных вариационных рядов определение моды

имедианы по интервальным рядам требует более сложных расчетов. Если предположить, что интервалы вариационного ряда имеют

одинаковую длину h и (xi ; xi+1) – модальный интервал, т.е. интервал,

435

где mi−1 , mi+1 – частоты, которые соответствуют предмодальному и

послемодальному интервалам.

Чтобы найти медиану интервального вариационного ряда, вначале также следует определить медианный интервал. Медианным называют первый интервал, накопленная частота которого превышает или равна половине общей суммы абсолютных частот, т.е.

Тогда медиана me вычисляется по формуле

где h и mме – длина и частота mi медианного интервала, соответственно.

Пример 3. Обследование качества пряжи на прочность дало следующие результаты:

Найти моду и медиану выборки.

Решение. Модальным интервалом является интервал (180; 200), ему соответствует частота mi = 58 . Следовательно, в формуле (4) следует

положить: xi = 180, h = 20, mi−1 = 19, mi+1 = 53 .

Получим

Для нахождения медианы воспользуемся формулой (6). Вначале с помощью неравенств (5) найдем медианный интервал. Нетрудно посчитать, что сумма всех частот равна n = 180 . Таким образом, неравенства (5) имеют вид

436

Если положить i = 5, то

4

åmj =1+ 6 +19 + 58 = 84 ,

j=1

5

åmj = 84 + 53 =137

j=1

и будем иметь

84 < 90 < 137.

Следовательно, медианным является интервал (200; 220),

mме = 53 и

me = 200 + 2053 (90 - 84) »102,3 . □

30. Моменты вариационного ряда. Моменты вариационного ряда определяются аналогично соответствующим характеристикам случайной величины из п.10.5.40.

Начальным моментом r-го порядка выборки называется величина

где x – среднее значение выборки.

437

Легко видеть, что

40. Асимметрия и эксцесс. Асимметрией распределения выборки называют величину

α= σμ€€33 ,

аэксцесс определяют следующим образом:

ε= σμ€€44 - 3.

Асимметрия и эксцесс характеризуют форму распределения. При симметричном распределении вариант в вариационном ряду равноудаленные от x варианты будут иметь одинаковую частоту и μ€3 = 0 , а следовательно, и α = 0 . Если в вариационном ряду

преобладают варианты меньшие, чем средняя x , то α < 0 и ряд будет отрицательно асимметричен, т.е. будет наблюдаться более длинная ветвь влево. Положительная асимметрия (более длинная ветвь вправо)

438

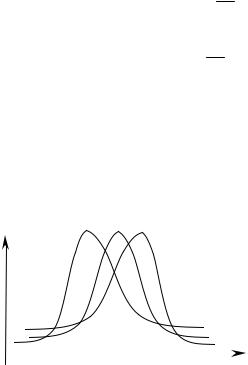
Эксцесс характеризует высоту вершины эмпирической кривой распределения по сравнению с нормальной кривой. Как известно,

439

50. Аппроксимация выборочного распределения. После построения гистограммы распределения случайной величины X нужно знать приближенное аналитическое представление неизвестного закона распределения X.

В случае непрерывной случайной величины X такое представление полезно по следующим причинам: а) аналитический вид плотности распределения сглаживает выборочный ряд наблюдений и дает представление о стохастической природе механизмов изучаемого явления; б) аналитическое представление позволяет интерполировать н а б л ю д е н и я .

Таким образом, возникает задача выбора аналитического вида аппроксимирующего распределения. Аппроксимирующую функцию можно выбрать различными способами, например, можно взять

полинома, тем точнее он описывает гистограмму. К аппроксимации плотности распределения обычно предъявляют следующие требования: аналитический вид должен соответствовать предполагаемому закону распределения, число параметров распределения не должно быть слишком велико (как правило, не более четырех).

Для выбора кривой аппроксимирующей функции иногда применяют метод моментов, суть которого состоит в следующем. Пусть X – непрерывная случайная величина и f (x) – ее неизвестная плотность распределения. Требуется по выборке найти ее оценку f€(x) .

чтобы наилучшим образом приблизить f€(x) к f (x) . Определим меру близости f€(x) к f (x) числом y:

−∞

440

Для наилучшей оценки коэффициентов b0 ,b1,...,bk следует потребовать, чтобы y из (10) была наименьшей, как функция переменных b0 ,b1,...,bk .

−∞

решить поставленную задачу.

§ 3. Статистические оценки параметров распределения

Приведем основные характеристики оценок параметра и дадим точечные статистические оценки математического ожидания и дисперсии. Изложим метод интервальной оценки математического ожидания случайной величины с известной дисперсией.

10. Оценки параметров. Состоятельность, несмещенность и эффективность оценки. Как указывалось выше, задачей статистики является описание характера распределения некоторого признака в генеральной совокупности на основании изучения этого признака у некоторой части совокупности (выборки), полученной в результате случайного отбора.

441

При этом распределение относительных частот в выборке рассматривается как эмпирическое приближение к теоретическому распределению вероятностей в генеральной совокупности. Выяснение закона распределения по данным выборки и составляет главную проблему математической статистики, так как на основании закона распределения изучаемого признака можно решать задачи по анализу и предсказанию результатов массового процесса. На практике часто теоретический закон распределения случайной величины в генеральной совокупности известен (или построено его приближенное аналитическое представление), т.е. известно, что закон распределения принадлежит к тому или иному семейству (нормальный закон, закон Пуассона и т.д.), зависящему от одного или нескольких параметров. Если бы точные значения параметров были известны, например, a и σ при нормальном законе, λ при законе Пуассона, то и закон распределения был бы полностью определен. Поэтому именно для определения этих параметров и проводится само статистическое исследование.

На основании закона больших чисел в форме Чебышева можно приближенно найти параметр a (математическое ожидание), положив его равным выборочному среднему. Аналогично можно рассматривать выборочную дисперсию как оценку теоретической дисперсии. Это означает, что будет найдена с некоторым приближением функция нормального закона распределения вероятностей.

Таким образом, задача оценивания неизвестного параметра θ состоит в построении приближенных формул

θ€ θ€(x1, x2 ,K, xn ) .

Функцию θ€= θ€(x1, x2 ,K, xn ) называют выборочной функцией или

статистикой, а ее значение в приближенном равенстве – оценкой. Любая выборка является случайной. Следовательно, все

выборочные функции θ€= θ€(x1, x2 ,K, xn ) также являются случайными.

Поэтому оценку θ€ неизвестного параметра θ будем рассматривать как случайную величину, а ее значение, вычисленное по данной выборке объема n, – как одну реализацию случайной величины.

Оценки параметров подразделяются на точечные и интервальные. Точечная оценка параметра θ определяется одним числом θ€. Интервальная оценка определяется двумя числами θ€1 и θ€2

442

– концами интервала, внутри которого содержится неизвестный параметр θ.

Естественно стремиться, чтобы оценка θ€ была в определенном смысле близка к истинному значению параметра θ.

Как определить близость оценки θ€ к истинному значению θ и как проверить качество этой оценки? С этой целью формулируются определенные требования к статистическим оценкам: состоятельность,

несмещенность и эффективность. Оценка θ€ называется состоятельной, если при увеличении числа испытаний эта оценка сходится по вероятности к истинному значению параметра θ, т.е.

Это свойство является желательным, но не обязательным. Иногда полученная оценка бывает смещенной, т.е. содержащей систематическую ошибку, но ее можно изменить так, чтобы она стала несмещенной.

Рассматривают также асимптотически несмещенные оценки, т.е. такие,

что Mθ€→θ при увеличении объема выборки.

Наконец, оценка θ€ называется эффективной, если она имеет наименьшую дисперсию по сравнению с другими оценками. Другими

словами, оценка θ€ будет эффективной, если при рассмотрении всех выборок данного объема n она будет иметь минимальную дисперсию.

20. Точечные оценки математического ожидания и дисперсии.

Пусть из генеральной совокупности образуется повторная выборка объема n со значениями признака x1, x2 ,..., xn . Для простоты

рассуждений будем полагать, что эти значения различны. В качестве оценки математического ожидания a генеральной совокупности будем брать выборочное среднее

443