
Tom_2
.pdfПРЕДИСЛОВИЕ
Настоящая книга является вторым томом учебника «Математика для инженеров».В данном томе излагаются основы числовых и функциональных рядов; кратных и поверхностных интегралов; теории поля; основы функций комплексной переменной; уравнений математической физики и операционное исчисление; элементы теории вероятностей и математической статистики.
При изложении материала книги авторы руководствовались следующими принципами: высокий уровень строгости и одновременно простота и доступность изложения; хорошая теоретическая подготовка и выработка навыков по применению теоретических знаний; соблюдение той степени общности, которая позволит учесть запросы каждого из конкретных направлений программы подготовки инженеров-специалистов и, тем самым, на основе излагаемого материала построить курс «Математика» для студентов различных инженерных специальностей.
Книга состоит из глав и параграфов, где изложены математические понятия и теоремы. Сложные доказательства некоторых теорем, как и предусмотрено программой, в книге не приводятся. Делается акцент на разъяснение смысла формулировок, понятий, иллюстрацию их примерами. Изложение теоретического материала сопровождается примерами и задачами с их подробным решением, а также упражнениями, позволяющими глубже проанализировать данный теоретический материал. В конце каждой главы приведены задачи для самостоятельного решения. В конце книги помещен предметный указатель.
В связи с профессиональной направленностью курса математики почти во всех главах ученика рассмотрены задачи из области физики и техники. Это будет способствовать формированию у студентов уверенности в п р о ф е с с и о н а л ь н о й з н а ч и м о с т и и з у ч а е м о г о п р е д м е т а .
Второй том имеет ту же структуру, что и первый, и здесь использована та же система ссылок. Например, выражение «по формуле (2.3.1)» означает, что эта формула под номером один находится в третьем параграфе второй главы.
Авторы надеются, что предложенная схема построения учебника будет полезной и студентам с разными требованиями к объему математических знаний, и преподавателям, владеющим предметом, а сама книга будет содействовать повышению математической культуры читателя.
Авторы выражают искреннюю благодарность рецензенту доктору физико-математических наук, профессору Кротову В.Г., коллективу кафедры математических методов теории управления БГУ, и рецензенту доктору физико-математических наук, профессору Рябушко А.П. за полезные советы и ценные замечания, которые помогли значительно улучшить содержание рукописи книги.
4

ГЛАВА 1
ЧИСЛОВЫЕ РЯДЫ
§ 1. Числовой ряд и его сумма
10. |
Понятие числового |
ряда. Пусть |
{a |
} |
– числовая |
последовательность, где an , |
n . |
n |
|
|
|
|
|
|
|||
Выражение вида |
∞ |
|
|
|
|
|
|
|
|
|
|
|
a1 + a2 + a3 +K + an +K = åan |
|
(1) |
||
|
|
n=1 |
|
|
|
называется числовым рядом. Числа a1,a2 ,...,an ,... |
называются членами |
||||
ряда, а an |
– n-ым или общим членом ряда (1). |
|
|
|
|
Сумма первых n членов ряда (1) называется n-ой частичной суммой данного ряда и обозначается Sn :
n
Sn = a1 + a2 + a3 +K+ an = åak .
k=1
Имеем
S1 = a1, S2 = a1 + a2 , S3 = a1 + a2 + a3,K, Sn = a1 + a2 +K + an ,K.
Рассмотрим последовательность частичных сумм ряда (1)
S1, S2 ,K, Sn ,K.
Если последовательность частичных сумм {Sn} имеет конечный
предел S, то числовой ряд (1) называется сходящимся, а число S называется суммой ряда (1):
|
∞ |
|
S = lim Sn или S = åan . |
|
|
n→∞ |
n=1 |
|
Если же предел последовательности {Sn } |
не существует или |
|
бесконечен, то ряд (1) называется расходящимся. |
{ xn } , где xn R , |
|
Обратно, с каждой последовательностью |
||
n N , можно связать ряд |
|
|
x1 + (x2 − x1) + (x3 − x2 ) + ... + (xn − xn−1) + ...,
для которого частичными суммами будут последовательные значения x1, x2 ,..., xn ,...
5

и при этом сумма указанного ряда совпадает с пределом последовательности { xn } .
Иными словами, рассмотрение ряда и его суммы − своеобразный перевод на другой язык изучения последовательности и ее предела, имеющей, как будет показано позже, свои преимущества как при установлении самого существования предела, так и при его вычислении.
Пример 1. Исследовать на сходимость ряд
1+ q + q2 +K + qn +K, q Î .
Решение. Составим его n-ую частичную сумму
Sn =1+ q + q2 +K + qn−1 .
Известно, что сумма первых n членов геометрической
прогрессии равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Sn = |
1- qn |
, |
q ¹ 1, и lim Sn = lim |
1- qn |
= |
1 |
lim (1- qn ) . |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1- q |
n→∞ |
n→∞ |
1- q |
|
|
|
1- q n→∞ |
|
||||||||||||
Если |
|
q |
|
<1, |
то lim (1- qn ) =1 и |
S = lim Sn |
= |
|
|
1 |
, т.е. |
||||||||||
|
|
|
|
||||||||||||||||||
|
|
1 |
- q |
||||||||||||||||||
|
|
|
|
|
|
|
n→∞ |
|
1 |
|
|
n→∞ |
|
|
|||||||
|
|
|
|
|
|
1+ q + q2 +K + qn +K = |
|
, |
|
q |
|
<1 . |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1- q |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Получили известную формулу суммы бесконечной убывающей геометрической прогрессии.
Если q >1 или q =1, то, очевидно, последовательность {Sn} является бесконечно большой последовательностью, если же q = −1, то предел {Sn} не существует. □
Выражение вида
∞ |
|
ai+1 + ai+2 +K = å ak |
(2) |
k=i+1
также представляет собой ряд. Он называется i-ым остатком ряда (1) и обозначается ri .
|
Теорема 1. Числовой ряд и любой его остаток сходятся или |
|
расходятся одновременно. |
|
|
|
Доказательство. По определению, n-ая частичная сумма ряда |
|
( |
1 |
) |
|
Sn = a1 + a2 +K + an , |
|
аm-ая частичная сумма ряда (2)
σm = ai+1 + ai+2 +K + ai+m .
6
Следовательно, σm = Si+m − Si .
Так как i фиксировано, то предел {σm} существует тогда и
только тогда, когда существует lim Si+m , т.е. последовательность
m→∞
S1, S2 ,K, Sn ,K имеет предел. □
Из этой теоремы следует, что сходимость ряда не нарушается, если изменить конечное число его членов.
Заметим также, что, если ряд (1) сходится, то
n |
∞ |
|
S = åak + |
å ak или S = Sn + rn , |
(3) |
k=1 |
k=n+1 |
|
где Sn – n -ая частичная сумма ряда (1), rn – его n-ый остаток.
|
|
|
|
|
|
∞ |
|
|
|
|
|
Теорема 2. |
Если ряд |
åan |
сходится к |
S , то сходится ряд |
|||||||
∞ |
|
|
|
|
∞ |
n=1 |
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|||
åk an , k = const |
и |
kS = åkan . Если же сходятся ряды |
åan и |
||||||||
n=1 |
|
|
|
|
n=1 |
|
|
|
|
n=1 |
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
åbn , и их суммы равны S и σ, соответственно, то сходится ряд |
|||||||||||
n=1 |
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
å(an ± bn ), |
и его сумма равна S ± σ . |
|
|
|
|||||||
n=1 |
|
|
|
|
|
|
|
|
|
|
|
Доказательство |
второго |
утверждения |
теоремы |
2. |
Пусть |
||||||
n |
|
|
|
|
n |
|
|
∞ |
n |
|
|
Sn = åak |
и |
σn = åbk . |
Тогда: |
å(an ± bn ) = lim å(ak ± bk ) = |
|||||||
k=1 |
|
|
|
k=1 |
|
|
n=1 |
n→∞ k=1 |
|
||
n |
|
|
n |
|
|
|
|
|
|
|
|
= lim åak ± lim åbk |
= lim Sn ± lim σn = S ± σ . □ |
|
|
||||||||
n→∞ k=1 |
n→∞ k=1 |
|
n→∞ |
n→∞ |
|
|
|
||||
Заметим, |
что |
утверждение, |
обратное |
доказанному, |
вообще |
||||||
|
|
|
|
|
|
|
∞ |
|
|
∞ |
|
говоря, неверно. |
Например, |
ряд |
å(1−1) сходится, а |
ряды å1 , |
|||||||
|
|
|
|
|
|
|
n=1 |
|
|
n=1 |
|
∞
å(−1) расходятся.
n=1
Упражнение 1. Доказать первое утверждение теоремы 2.
20. Необходимое условие сходимости числового ряда.
7

|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
Теорема 3. Если ряд åan |
сходится, то |
|
|
||||||||||
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim a = 0 . |
|
|
|
(4) |
||
|
|
|
|
|
|
|
n→∞ |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
сходится, тогда lim Sn = S . |
|||
Доказательство. |
Пусть ряд |
åan |
|||||||||||
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно, S |
n |
- S |
n−1 |
= a |
n |
и |
lim a |
n |
= lim S |
n |
- lim S |
n−1 |
= S - S = 0 . □ |
|
|
|
|
n→∞ |
n→∞ |
n→∞ |
|
||||||
Итак, если ряд сходится, то его общий член стремится к нулю
при n → ∞ . Отсюда следует, что, если lim an ¹ 0 или не существует,
n→∞
∞ |
|
|
|
|
|
|
|
|
|
|
|
то ряд åan расходится. |
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
Однако, условие (4) не является достаточным, т.е., если оно |
|||||||||||
выполняется, то это не означает, что ряд сходится. |
|
||||||||||
Пример 2. Исследовать на сходимость гармонический ряд |
|
||||||||||
|
1 |
|
1 |
|
|
1 |
|
∞ |
|
||
1+ |
+ |
+L + |
+L = å |
1 |
. |
(5) |
|||||
|
|
|
|
||||||||
2 |
3 |
|
n |
n=1 n |
|
||||||
Решение. Необходимое |
условие |
сходимости числовых |
рядов |
||||||||
выполняется: lim 1 = 0 . Однако, этот ряд расходится. Действительно,
n→∞ n
предположим противное. Пусть ряд (5) сходится и lim Sn = S . Тогда: |
|||
|
|
n→∞ |
|
lim (S2n - Sn ) = lim S2n - lim Sn = S - S = 0 . |
(6) |
||
n→∞ |
n→∞ |
n→∞ |
|
С другой стороны,
S2n - Sn = n1+1 + n +1 2 +L+ 21n ³ n +1 n + n +1 n +L+ 21n = n 21n = 12 ,
что противоречит (6). Следовательно, гармонический ряд расходится.
□
Пример 3. Исследовать сходимость ряда
∞ |
1 |
|
|
|
ånsin |
. |
(7) |
||
|
||||
n=1 |
n |
|
||
Решение. Проверим выполнение необходимого условия сходимости ряда:
8
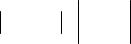
|
|
|
1 |
|
|
|||
|
1 |
|
sin |
|
|
=1 ¹ 0 . Значит, ряд (7) расходится. □ |
||
lim nsin |
= lim |
n |
||||||
n |
|
|
|
|||||
n→∞ |
n→∞ |
1 |
|
|
|
|
||
|
|
|
|
n |
|
|
||
§ 2. Критерий Коши. Достаточные признаки сходимости знакопостоянных рядов
Необходимый признак сходимости в общем случае не дает возможности судить о том, сходится данный ряд или нет. Поэтому нужно иметь критерии сходимости рядов или установить достаточные условия сходимости.
Рассмотрим знакоположительный ряд
∞ |
|
åan , an ³ 0, nÎ . |
(1) |
n=1
Отметим, что знакоотрицательный ряд, т.е. ряд с неположительными членами переходит в знокоположительный путем умножения его на (−1) , что, в силу теоремы 2, не влияет на
сходимость ряда.
10. Критерии сходимости ряда (1).
Теорема 1. Для того, чтобы ряд (1) сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограниченной.
Доказательство достаточности. Пусть последовательноcть {Sn} ограничена. Заметим, что Sn+1 = Sn + an+1 ³ Sn , nÎ N , так как an ³ 0 . Тогда последовательность {Sn} – неубывающая и ограничена. Значит, по теореме Вейерштрасса, она имеет предел. □
Упражнение 1. Доказать необходимость условий теоремы 1. Наличие общего критерия Коши для сходимости числовой
последовательности позволяет установить соответствующий критерий и для числового ряда.
Теорема 2. Для сходимости ряда (1) необходимо и достаточно, чтобы для любого ε > 0 существовал номер N(ε ) такой, что при
всяком натуральном p и всех n > N(ε ) имело место неравенство
n+ p
Sn+ p - Sn = å am < ε . m=n+1
9

Доказательство. Утверждение теоремы 2 равносильно критерию Коши для сходимости последовательности {Sn} частичных сумм ряда, что, согласно определению, и есть сходимость ряда (1). □
20. Признаки сравнения рядов. Сходимость или расходимость знакоположительного ряда (1) часто можно установить путем сравнения его с другим («эталонным») рядом, о котором известно, сходится он или нет.
Теорема 3 (признак сравнения). Пусть даны два ряда с
∞ |
∞ |
неотрицательными членами åan (обозначим (А)) и |
åbn |
n=1 |
n=1 |
(обозначим (В)), и пусть n N |
|
an ≤ bn . |
(2) |
Тогда из сходимости ряда (В) следует сходимость ряда (А), а из расходимости ряда (А) – расходимость ряда (В).
Доказательство. Обозначим n-е частичные суммы рядов (А) и (В), соответственно, Sn(1) и Sn(2) . Из неравенства (2) следует, что
|
|
|
Sn(1) ≤ Sn(2) . |
|
(3) |
|
Пусть ряд (В) сходится, тогда |
lim Sn(2) = S2 . Следовательно, с |
|||||
|
|
|
|
n→∞ |
|
|
учетом |
неравенства |
(3), |
lim Sn(1) |
≤ lim Sn(2) ≤ S2 , |
т.е. |
|
|
|
{Sn(1)} |
|
n→∞ |
n→∞ |
|
последовательность |
неубывающая |
и ограничена |
сверху. |
|||
Поэтому, по теореме Вейерштрасса, |
lim Sn(1) |
существует. Значит, ряд |
||||
(А) сходится. |
|
|
n→∞ |
|
|
|
|
|
|
|
|
||
Пусть теперь ряд (А) расходится. Так как члены ряда |
||||||
неотрицательны, то |
lim Sn(1) |
= ∞ . С учетом неравенства (3), получаем |
||||
|
|
n→∞ |
|
|
|
|
lim S(2) = ∞ , т.е. ряд (В) расходится. □
n→∞ n
Замечание 1. Теорема 3 справедлива и в том случае, когда неравенство (2) выполняется не для всех членов рядов (А) и (В), а начиная с некоторого номера N. Это вытекает из теоремы 1.1.
Теорема 4 (предельный признак сравнения). Пусть даны два знакоположительных ряда (А) и (В). Если существует конечный,
отличный от нуля, предел lim an = A (0 < A < ∞) , то ряды (А) и (В)
n→∞ bn
одновременно сходятся или расходятся.
10

Доказательство. По определению предела |
"ε > 0 |
$Nε Î , |
|||
что при n ³ Nε выполняется неравенство |
an |
- A |
< ε |
или |
|
|
|
||||
|
bn |
|
|
|
|
(A - ε)bn < an < (A + ε )bn , n ³ Nε . |
|
(4) |
|||
Если ряд (А) сходится, то, согласно левому неравенству (4) и |
|||||
∞ |
|
|
|||
теореме 3, ряд å(A - ε)bn также сходится. Но |
тогда, |
согласно |
|||
n=1
теореме 1.2, ряд (В) сходится.
Если ряд (А) расходится, то, согласно правому неравенству (4), теореме 3 и теореме 1.2, ряд (В) расходится.
Аналогично, если ряд (В) сходится (или расходится), то сходящимся (или расходящимся) будет и ряд (А). □
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1. Исследовать сходимость ряда å |
1 |
, |
p <1. |
|
|
|
|
|
|
||||||||||||
|
|
|
|
p |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Применим признак сравнения, воспользовавшись тем, |
|||||||||||||||||||||
что |
|
|
гармонический ряд |
расходится. |
Очевидно, |
что |
1 |
|
³ |
1 |
, |
||||||||||||||
|
|
|
np |
|
|
||||||||||||||||||||
n , |
p ≤ 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
||
|
|
|
|
Ряд å |
1 |
расходится, поэтому расходится и ряд å |
1 |
, |
|
p £1. |
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
□ |
|
|
|
|
n=1 n |
|
|
|
|
|
|
|
|
|
|
n=1 n p |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Можно |
показать, что |
ряд |
å |
1 |
при |
p >1 |
сходится. |
|
Ряд |
||||||||||||
|
|
|
|
p |
|
||||||||||||||||||||
∞ |
|
|
|
|
|
|
|
|
n=1 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
å |
|
|
называется рядом Дирихле. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
n=1 n |
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|||
|
|
|
|
Пример 2. Исследовать сходимость ряда åtg |
. |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
3n |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
Решение. Применим предельный признак сравнения. Поскольку |
|||||||||||||||||||||
|
|
|
tg |
π |
= π ¹ 0 и гармонический |
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
3n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
lim |
|
|
|
ряд |
å |
1 |
расходится, |
|
то, по |
||||||||||||||||
|
|
1 |
n |
|
|||||||||||||||||||||
n→∞ |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
n=1
n
теореме 4, расходится и исходный ряд. □
30. Признаки Д’Аламбера и Коши.
11

∞
Теорема 5 (признак Д’Аламбера). Пусть дан ряд åan с
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
||
положительными |
членами |
и существует предел |
|
lim |
an+1 |
= q , |
|||||||||||
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
an |
|||||
тогда при q <1 ряд сходится, а при q >1 ряд расходится. |
|
|
|
|
|
||||||||||||
Доказательство. Пусть q <1 . Выберем число ε > 0 так, чтобы |
|||||||||||||||||
q + ε <1 . По |
определению |
предела |
последовательности, |
N0 |
|||||||||||||
|
|
|
n > N0 выполняется |
|
an+1 |
− q |
|
< ε или |
|||||||||
такой, что |
неравенство |
|
|||||||||||||||
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
an |
|
|
|
|
|
|||
q − ε < |
an+1 |
< q + ε . |
Таким образом, |
n > N |
0 |
имеем a |
n+1 |
< (q + ε )a . |
|||||||||
|
|||||||||||||||||
|
an |
|
|
|
|
|
|
|
|
|
|
n |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
aN0 +2 < (q + ε )aN0 +1 , |
aN0 +3 < (q + ε )aN0 +2 < (q + ε )2 aN0 +1, |
||||||||||||||||
aN0 +4 < (q + ε )aN0 +3 < (q + ε )3 aN0 +1 и т. д.
Ряд (q + ε) aN0 +1 + (q + ε )2 aN0 +1 + (q + ε )3 aN0 +1 +K сходится, так как q + ε (0,1) . Следовательно, по признаку сравнения, сходится и
∞ |
+∞ |
ряд å |
an , а с ним и ряд åan . |
n=N0 +2 |
n=1 |
Случай q >1 доказывается аналогично. □ Упражнение 2. Доказать теорему 5 в случае q >1.
Если же q =1, то ряд может сходиться, а может и расходиться.
|
|
|
|
|
|
∞ |
Теорема 6 (признак Коши с корнем). Если для ряда åan с |
||||||
|
|
|
|
|
|
n=1 |
неотрицательными членами существует предел lim |
n |
|
= q , то при |
|||
a |
||||||
|
|
|
n→∞ |
|
n |
|
q <1 ряд сходится, при q >1 ряд расходится. |
|
|
|
|||
Доказательство. По условию, lim |
n |
|
= q . Пусть q <1 . По |
|||
a |
||||||
n→∞ |
|
n |
|
|
|
|
|
|
|
|
|
|
|
теореме о связи функции, ее предела и бесконечно малой величины,
n |
|
= q +α, |
α → 0 |
при |
n → ∞. |
Отсюда, |
a |
|
= (q +α)n , |
но при |
|
a |
n |
||||||||||
|
n |
|
|
|
|
|
|
|
∞ |
||
|
|
|
|
|
|
|
an < ρn . |
|
|||
больших n |
имеем |
q +α < ρ <1, |
поэтому |
Ряд |
åρn , |
||||||
представляющий собой |
сумму |
членов бесконечно |
|
n=1 |
|||||||
убывающей |
|||||||||||
12
геометрической прогрессии, сходится. В силу признака сравнения, ряд
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
åan |
также сходится. При q >1 доказательство аналогично. □ |
|
|
|||||||||||||||||||||
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Упражнение 3. Доказать теорему 6 при q >1. |
|
|
|
|
|
|
||||||||||||||||
|
|
Пример 3. Исследовать сходимость следующих рядов: |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
∞ |
|
2n |
|
|
∞ æ 2n +1 |
ön |
|
|
|
|
|
|
||||
|
|
|
|
|
|
a) |
å |
|
|
; |
б) |
åç |
|
|
|
|
÷ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
n=1 n! |
|
|
n=1è n |
+ 2 |
|
ø |
|
|
|
|
|
|
||||
|
|
Решение. а) Применим признак Д’Аламбера. Имеем: |
|
|
|
|
||||||||||||||||||
|
2n |
|
|
2n+1 |
|
|
|
|
a |
|
|
|
2n+1n! |
|
|
2 |
|
|
|
|||||
a = |
|
|
, |
a |
= |
|
|
, |
q = lim |
n+1 |
= lim |
|
|
|
|
= lim |
|
|
|
= 0 |
<1. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
n |
|
n! |
n+1 |
|
(n +1)! |
|
|
|
n→∞ |
an |
n→∞ (n +1)!2n n→∞ n +1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
Исходный ряд сходится.
б) К данному ряду удобно применить признак Коши:
|
|
|
|
|
|
|
1 |
|
|
|
2 + |
1 |
|
|
|
|
|
|
é |
|
|
|
n ù |
|
|
|
|
|
|
||
|
|
|
2n +1 |
|
n |
|
2n +1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
q = lim |
n |
a |
= lim êæ |
ö |
ú |
|
= lim |
= lim |
|
n |
= 2 >1 . |
||||
|
|
÷ |
|
|
|
||||||||||
n→∞ |
|
n |
ç |
n + 2 |
|
|
n→∞ n + 2 n→∞ |
|
2 |
|
|
||||
|
|
n→∞ êè |
ø ú |
|
|
|
|
||||||||
|
|
|
ë |
|
|
|
û |
|
|
|
|
1+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|||||
Исходный ряд расходится. □
Теорема 7 (интегральный признак Коши). Если члены
∞
знакоположительного ряда åan монотонно убывают и существует
n=1
положительная невозрастающая функция f (x) , такая, что f (n) = an
∞
при n ³1 , то ряд и несобственный интеграл ò f (x)dx сходятся или
1
расходятся одновременно.
Доказательство. По условию, f (n +1) < f (n) . Согласно теореме об оценке определенного интеграла, имеем
k+1
f (k +1) £ ò f (x)dx £ f (k), k =1, 2,K .
Суммируя |
|
k |
неравенства по k, получаем |
|
полученные |
||||
n |
n+1 |
|
n |
|
å f (k +1) £ |
ò f (x)dx £å f (k) или |
|||
k=1 |
1 |
n+1 |
k=1 |
n+1 |
n+1 |
|
n |
||
å ak £ |
ò |
f (x)dx £åak , |
Sn+1 - a1 £ ò f (x) dx £ Sn . |
|
k=2 |
|
1 |
k=1 |
1 |
13
