Tom_2

Так как P = xy = u5v - u2v4 , Q = yz = u3v3, R = zx = u4v2 - uv5,

будем иметь

154

(u,v) W.

Следовательно, по формуле (4) поток

11

П= -òòDdu dv = òduò(-3u8v2 - 3u7v3 + 6u6v4 - 3u5v5 +3u4v6 + 3u3v7 +

= - 19 - 323 + 356 - 121 + 353 + 323 + 92 = 1260359 . □

20. Поток вектора через замкнутую поверхность. Формула Остроградского. Если поверхность S замкнута, то в качестве нормали к ней возьмем внешнюю нормаль.

Теорема 1 (Остроградского). Если в некоторой пространственной области V координаты P, Q, R вектора a

непрерывны и имеют непрерывные частные производные

¶¶Px , ¶¶Qy , ¶¶Rz , то поток вектора a через замкнутую кусочно-гладкую

поверхность S, расположенную в области V, равен тройному интегралу по области V, ограниченной этой поверхностью, то есть

Доказательство. Пусть замкнутая поверхность S ограничена поверхностями S1 и S2 , являющимися графиками функций z1 = f1(x, y) , z2 = f2 (x, y) соответственно, и цилиндрической

155

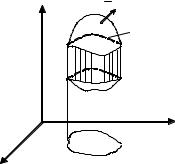
поверхностью S3 с направляющей − границей области D (проекции поверхности S на плоскость Oxy ) и образующей, параллельной оси

Oz (рис. 2). Пользуясь формулой (4.4.1) приведения тройного интеграла к повторному, будем иметь:

òòR(x, y, z)dx dy = òò(0 ×α + 0× β + R ×0)ds = 0.

Прибавляя к поверхностным интегралам в формуле (6) равный нулю интеграл òòR(x, y, z) dx dy, будем иметь

+òòR(x, y, z)dx dy =òòR(x, y, z)dx dy.

Складывая формулы (6΄) и (7), получим формулу (5). □

Формула (5) называется формулой Остроградского.

156

Пусть a – поле скоростей движения несжимаемой жидкости. Если П = 0 , то это означает, что из объема V, ограниченного поверхностью S, вытекает столько жидкости, сколько и прибывает в него. Если П > 0 , то жидкости вытекает больше, чем прибывает. Это

S: {x2 + y2 + z2 = 2Rz, 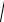x2 + y2 = z3} .

Решение. Подставляя a в формулу (5), получим, что поток поля a равен: П = òòò3z2dxdydz , где область V изображена на рис. 3.

157

30. Дивергенция векторного поля. Количественной характеристикой векторного поля a является дивергенция (расходимость).

Рассмотрим векторное поле a = Pi + Qj + Rk и выделим в нем

малое тело V объемом v , ограниченное замкнутой поверхностью S . Предел отношения потока вектора a через поверхность S к объему v при стягивании объема v в некоторую точку M V

называется дивергенцией вектора a в точке M или расходимостью и обозначается diva(M ) .

координат в пространстве, поэтому оно называется инвариантным определением.

Вычислим дивергенцию в декартовой прямоугольной системе

по x, y, z , соответственно, функции в области V.

Используя формулу Остроградского, определение (8) и теорему о среднем значении для тройного интеграла, получим

Как видно из определения, дивергенция векторного поля в точке является скалярной величиной. Она образует скалярное поле в данном векторном поле.

Исходя из физического смысла потока (условно считается, что a(M ) есть поле скоростей фиктивного стационарного потока

несжимаемой жидкости), можно сказать, что: при div a(M ) > 0 точка

следует из равенства (8), величина div a(M ) характеризует мощность (интенсивность, плотность) источника или стока в точке M . В этом

158

состоит физический смысл дивергенции. Понятно, что, если в объеме V , ограниченном замкнутой поверхностью S , нет ни источников, ни стоков, то div a = 0 .

то есть поток вектора a через замкнутую поверхность равен тройному интегралу от дивергенции вектора по области, ограниченной этой поверхностью.

159

точках M некоторой области V, если дивергенция этого поля в этих точках равна нулю, т.е.

Соленоидальное поле не имеет в области V ни источников, ни стоков и обладает следующими свойствами.

1) В соленоидальном поле поток вектора a (M ) через любую

замкнутую поверхность S равен нулю.

Это свойство следует из формулы (10).

2) В соленоидальном поле потоки вектора через различные сечения векторной трубки равны между собой (принцип сохранения интенсивности векторной трубки).

Доказательство. Рассмотрим два сечения S1 и S2 векторной трубки (рис. 4), которые образуют вместе с боковой поверхностью S3 замкнутую поверхность S. Вследствие соленоидальности поля a , получим

160

П = òò(a, n)ds + òò(a, n)ds + òò(a, n)ds =

значит поток вектора a через любое сечение векторной трубки имеет одно и то же значение. □

С точки зрения гидродинамики этот факт означает следующее: если a − поле скоростей несжимаемой жидкости, то ее объем, протекающий через любое сечение векторной трубки в единицу времени, сохраняется неизменным.

3) В соленоидальном поле векторные линии не могут ни начинаться, ни оканчиваться внутри поля. Они либо замкнуты, либо начинаются и оканчиваются на границе поля, либо имеют бесконечные ветви (в случае неограниченного поля).

Упражнение 2. Установить справедливость свойства 3) соленоидального поля.

Пример 7. Определить, являются ли соленоидальными следующие поля:

1)a1(M ) = xi - 2yj - zk ;

2)a2 (M ) = x(z2 - y2 )i + y(x2 - z2 ) j + z(y2 - x2 )k .

поле a2 (M ) соленоидально. □

161

§3. Линейный интеграл, циркуляция и ротор векторного поля

10. Линейный интеграл в векторном поле. Пусть в области V

заданы непрерывное векторное поле a = Pi + Qj + Rk и

ориентированная гладкая линия L. Обозначим через τ единичный вектор касательной к линии L, направление которого совпадает с выбранным направлением на линии.

Линейным интегралом вектора a вдоль линии L называется криволинейный интеграл первого рода от скалярного произведения

г д е d l – д и ф ф е р е н ц и а л д л и н ы д у г и л и н и и L

( dl = 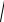(dx)2 + (dy)2 + (dz)2 ).

Линейный интеграл (1) может быть записан в различных видах.

+ R(x(t), y(t), z(t))z′(t))dt.

Если a − силовое поле, то линейный интеграл равен работе, которую поле совершает по перемещению материальной точки вдоль ориентированной кривой.

Вычисление линейного интеграла в случае плоского поля проводится по формулам (5.2.8).

162

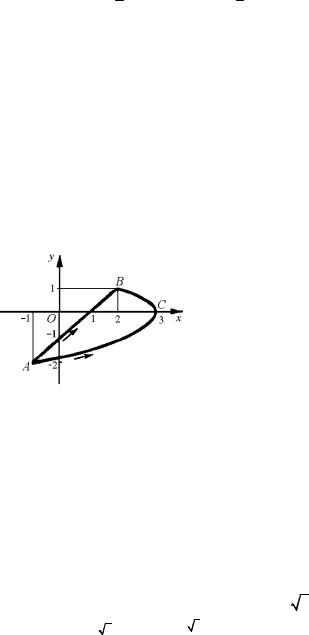
Пример 1. Вычислить линейный интеграл плоского векторного поля a = (2x − y2 +1) i + (3x + 2y2 −10) j по линии L, если L − дуга

параболы x = 3 − y2 , заключенная между точками A(–1;–2) и B(2;1),

(рис.1).

Решение. Согласно формуле (2), имеем

ò(2x − y2 +1)dx + (3x + 2y2 −10)dy ,

L

где линия L = ACB (рис. 1) задана уравнением x = 3 − y2 . Подставляя

x = 3 − y2 в выражение (2) и учитывая, что y изменяется вдоль L от –2 до 1, получаем

1

ò ((2(3 −y2 ) − y2 +1)(−2y) + (3(3 − y2 ) + 2y2 −10))dy =

−2

1

= ò (6y3 −y2 −14y −1)dy = −7,5 .