Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гродненский государственный университет им. Я. Купалы

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Tom_2

.pdf

Скачиваний:

Добавлен:

18.02.2016

Размер:

3.2 Mб

Скачать

☆

<<< < Предыдущая 23 24 25 26 27 28 29 30 31 32 33 3435 / 4935 36 37 38 39 40 41 42 43 44 45 46 47 > Следующая >>>

E ωch

æ lp ö

E ω

U (x, p) =

+ ω

æ lp ö

( p2 + ω2 )sh ç

l - x ö

a ø

sh ç p

= E0ω

a ø

æ lp ö

( p

+ ω

)sh ç

è a

Найдем оригинал u(x,t) для полученной функции U (x, p) ,

которая имеет простые полюсы в точках

±iω, ±

iakπ

(k = 1,2,...)

( p = 0 – устранимая особая точка для U (x, p) ). Используя формулы

(1.4) и (1.6), находим

u(x,t) =

Res

U (x, p)e

+ 2

∞

Res

(U (x, p)e

)

ω ç 2 Re

)÷

(

iakπ

è p=iщ

k=1

ç p=

l - x ö

ç sh ç p

l - x

ç sh p

sh lp

∞

p2 + ω2

= E0ω ç

2 Reç

+ 2åRe

÷ =

(p2

lp ö¢

+ ω2 )

k=1

p=iω

çsh

iakπ

a ø

l - x

iakπt

öö

sh çiω

÷eiωt

2a ∞

sh çikπ

÷e

÷÷

= E0ω ç Re

åReç

iωl

÷÷ =

iω sh

k=1

ω2

÷ch(ikπ ) ÷÷

÷÷

øø

l - x ö

ç i sin ç

(cosωt + isinωt) ÷

= E ω

ç Re

ωl

ω sin

l - x öæ

akπ t

∞

ç isin çkπ

÷çcos

+ isin

+ 2a åRe

øè

÷ =

a2k2π

k=1

ω2

2 ö

÷coskπ

344

l - x ö

kπ x

akπt ö

ç sin ç

÷sinωt

∞

sin

= E0

a ø

+ 2aωlå

÷ .

□

l2ω2 - a2k2π 2

sin

ωl

k=1

Таким образом, найдена функция u(x,t) , определяющая величину напряжения по истечению времени t от начального состояния.

Задания для самостоятельной работы

1.Установить, какие из данных функций являются оригиналами:

ì0	при t < 0;	ì0			при t < 0;
ï		ï
а) f (t) = í	при t > 0;	б) f (t) = í	t	2
ïe(3+i)t	при t > 0;		t		при t ³ 0.
î		ï2			при t ³ 0.
		î

2.Пользуясь определением, найти изображения функций:

а) f (t) = sin3t ; б) f (t) = ch(4 − 3i)t .

3.Используя свойства линейности и подобия, найти изображения оригиналов:

а) cos4 t - sin4 t ; б) sin2 5t ; в) cos3 2t .

4.Пользуясь свойствами смещения и запаздывания найти изображения оригиналов:

а)

ch 4t sin 3t ;

б)

e−2t cos2 t ; в) et−3 sin(t - 3) .

Найти оригиналы по их изображениям:

p - 3

e−2 p

а)

;

б)

;

2 p2 - 6 p -1

p2 + 4 p + 3

p3 ×e−2 p

в)

;

г)

p4 +13p2 + 36

( p2 + 9)2

С помощью вычетов найдите оригиналы для изображений:

а)

5p2 + 60 p +146

; б)

;

( p2 + 4)( p + 5)2

( p -1)3

4 - p - p2

в)

;

г)

p3 - p2

( p -1)3 ( p3 +1)

345

7.Решить следующие дифференциальные уравнения при заданных начальных условиях:

а)

x′′ + 2x′ + x = sin t,

x(0) = 0, x′(0) = -1;

б)

x′′′ + x′ = t,

x(0) = 0, x′(0) = -1,

x′′(0) = 0 ;

в)

- x

¢¢

¢¢¢

= 1, x(0) = x (0)

= x (0)

= x (0) = 0 .

С помощью формулы Дюамеля найти решение задачи Коши:

а)

x¢¢ - x¢ =

e2t

x(0) = x¢(0) = 0 ;

(

+ e

¢¢

+ x

б)

4 + tg2 t ,

x(0) = x (0) = 0 ;

в)

x¢¢¢ + x¢ =

x(0) = x¢(0) = x¢¢(0) = 0 .

2 + sin t

Решить системы уравнений при заданных начальных условиях

а)

ïx + x¢

= y + e

x(0) = y(0) = 1 ;

ïy + y

= x + e

б)

ìx¢ - y¢ - 2x + 2y = 1- 2t,

= 0 ;

¢ + x =

x(0) = y(0) = x (0)

îx¢¢ + 2y

ìx¢ = -y - z,

в) íï y¢ = -x - z,

x(0) = -1,

y(0) = 0, z(0) = 1 .

- y,

îz¢ = -x

10.Электрон вылетает из начала координат с начальной скоростью v0 , направленной по оси Ox . Найти закон движения электрона, предполагая, что напряжение магнитного поля H постоянно и направлено перпендикулярно к плоскости Oxy .

Указание. Уравнения движения электрона:

ì	&&	= -		eH			&
									&
ïmx					c		× y,	x(0) = 0,		= v0 ,
í									x(0)
			eH					y(0) = 0,	&	= 0.
ï	&&	=					&		y(0)
			c
îmy						× x,

346

11.Снаряд вылетает из орудия со скоростью v0 м/сек под углом 45° к горизонту. Найти, пренебрегая сопротивлением воздуха, наибольшую высоту, на которую поднимется снаряд, и место его падения.

Указание. Уравнение движения

{

= 0,

x(0) = 0,

= −gm,

y(0) = 0,

y(0)

2 .

12. Решить интегральные уравнения:

а)

y(t) = t +

ò(t −τ )2 y(τ )dτ ; б)

y(t) = cost + òet−τ y(τ )dτ ;

в)

òcos(t −τ )y(τ )dτ = sin t ; г) òch(t −τ )y(τ )dτ = sh t .

13.Найти ток i(t) в RC-цепи (последовательно включены

сопротивление R и емкость C) при подключении постоянной э.д.с. e(t) = E , если uC (0) = u0 .

14.Найти ток i(t) в RL-цепи (последовательно включены

сопротивление R и емкость L) при подключении постоянной э.д.с. e(t) = E .

15. Температура u(x,t) в тонком стержне удовлетворяет уравнению

∂u	= a2	∂2u	, a2	= const .
∂t		∂x2

Найти распределение температур в полупространстве x > 0 , если известен закон изменения температуры его левого конца, а

начальная температура стержня равна нулю:		u	t=0 = 0 ,


u	x=0 = f (t)	.

16.Стержень длины l находится в состоянии покоя, его конец закреплен. В момент времени t = 0 к свободному концу стержня приложена сила F (на единицу площади), направленная вдоль стержня. Найти колебания стержня.

Указание. Дифференциальное уравнение имеет вид

∂2u	=	1 ∂2u		, 0	≤ x ≤ l, t > 0 ,
∂x2		c2	∂t2

347

t=0 = 0,

¶u

= 0,

u(0,t) = 0,

¶u(l,t) =

F .

¶t

x=0

¶x

¶2u

17. Найти

решение

волнового

уравнения

¶x2

¶t2

удовлетворяющее

начальным

условиям u(x,0) = Acos

nπ x

¶u(x,0)

= 0 ,

0 ≤ x ≤ l ,

граничным

условиям

¶t

¶u(0,t)

¶u(l,t)

= 0 .

¶x

18. Найти решение уравнения теплопроводности удовлетворяющее

u(x,0) = 0, x ³ 0, u(0,t) = A, lim u(x,t) = 0 .

x→∞

¶2u = α 2 ¶u , ¶x2 ¶t

условиям

348

349

ГЛАВА 10

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

§ 1. Основные понятия теории вероятностей

Обозначим предмет теории вероятностей, дадим понятия события и его вероятности.

10. Предмет теории вероятностей. Большое количество явлений и фактов, встречающихся в повседневной жизни, имеют случайную природу. Например, выпадение герба при бросании монеты является случайным событием, однако при многократном бросании монеты выясняется, что примерно в половине случаев выпадает герб. Когда рассматриваются массовые количества однородных явлений или фактов, то вскрываются определенные закономерности. Изучение этих закономерностей и составляет предмет теории вероятностей и

основанной на ней математической статистики. При этом изучаемые явления рассматриваются в абстрактной форме, независимо от их конкретной природы, что дает возможность использования определенного математического аппарата. Установленные общие закономерности и положения могут применяться к широкому классу явлений.

20. Случайные события и вероятность. В основе теории вероятностей лежит понятие случайного эксперимента.

Эксперимент считается случайным, если он может закончиться любым из некоторой совокупности известных результатов, но до осуществления эксперимента нельзя предсказать, каким именно. Различные результаты эксперимента будем называть исходами.

Множество всех взаимно исключающих исходов эксперимента называется пространством элементарных событий. Взаимно исключающие исходы эксперимента – это те исходы, которые не могут наступить одновременно.

Исходы пространства элементарных событий называются элементарными событиями. Произвольное подмножество пространства элементарных событий будем называть случайным событием и обозначать А, В, С, …

Пространство элементарных событий будем обозначать Ω , а его элементы − ω . Если эксперимент заканчивается одним из элементарных событий ωk , входящих в случайное событие А, то говорят, что наступило событие А. Поэтому элементарные события,

350

входящие в событие А, называются благоприятствующими этому

событию.

Два случайных события имеют специальные названия: W называется достоверным событием (эксперимент обязательно заканчивается каким-то исходом), а − невозможным событием.

Случайные события могут быть получены из элементарных событий довольно сложным образом. Определим правила, по которым они образуются из элементарных событий.

Суммой событий А и В называется событие А+В, состоящее из всех элементарных событий, входящих либо в А, либо в В, то есть А+В= A È B . Другими словами, событие А+В состоит в том, что произошло хотя бы одно из событий А или В.

Произведением событий А и В называется событие АВ,

состоящее из всех элементарных событий, входящих и в А, и в В, т.е. AB = A Ç B . Другими словами, событие АВ состоит в том, что события А и В произошли одновременно.

Разностью событий А и В называется событие А–В, состоящее из всех элементарных событий, входящих в А, но не входящих в В, т.е. A − B = A \ B . Другими словами, событие А–В состоит в том, что событие А произошло, а событие В не произошло.

События А и В называются несовместными, если нет элементарных событий, входящих в А и В одновременно, т.е. AB = .

Это означает, что события А и В не могут произойти одновременно.

Событие

, состоящее из элементарных событий,

не входящих

в А,

называется противоположным к событию А, т.е.

= Ω \

A .

Другими словами, событие

состоит в том, что событие А не

Говорят, что событие А влечет событие В (и в этом случае

пишут A p B ), если

все

элементарные

события,

входящие в

А,

содержатся также и в В, т.е. A B . Другими словами,

это означает,

что при наступлении события А обязательно произошло и событие В. Рассмотрим простой пример. Пусть множество всех взаимно

исключающих исходов эксперимента Ω = {1,2,3,4,5,6} – множество

цифр k, выпадающих при бросании игральной кости (кубика).
Тогда событиями будут любые подмножества Ω , например, A = {1}		–
выпадение цифры 1, B = {2,4,6} – выпадение четной цифры и т.д. При
этом Ω является достоверным событием и	6
	Ω = U ωk , где ωk	–
выпадение цифры k, причем события ωk	k=1
	будут элементарными
событиями в данном эксперименте.

351

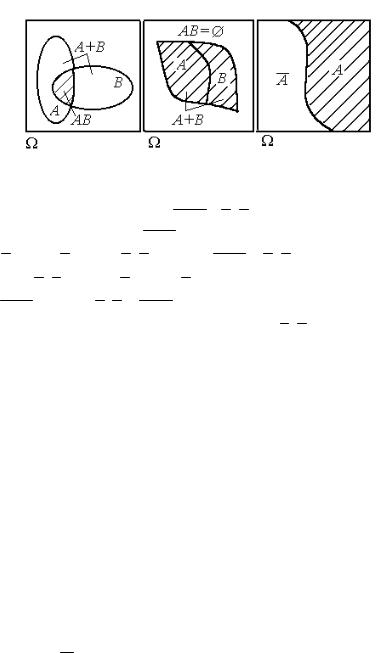
При решении задач, относящихся к событиям, полезно

использовать графические представления операций над множествами, изображенные на рис. 1.

Рис. 1

Пример 1. Доказать, что A + B = A× B .

Решение. Пусть ω Î A + B , тогда ω Ï A + B Þ ω Ï A и ω Ï B Þ ω Î A и ω Î B Þ ω Î A× B , значит, A + B Ì A× B . С другой стороны, если ω Î A× B , то ω Î A и ω Î B Þ ω Ï A и ω Ï B Þ ω Ï A + B Þ ω Î A + B , значит, A× B Ì A + B . □

Упражнение 1. Показать, что A + B = W \ ( A× B).

Пусть выделено некоторое подмножество событий F, причем операции сложения, умножения и вычитания не выводят из F. На этом множестве событий F и определяется вероятность. Числовая функция Р: F ® называется вероятностью, если выполнены следующие условия:

1)P(A) ³ 0 для любого события AÎF;

2)P(W) =1 (нормировка вероятности);

если

события

A, B ÎF

несовместны,

то

P(A + B) = P(A) + P(B) (аддитивность вероятности).

Вероятность не определяется однозначно указанной системой аксиом – на одном и том же пространстве элементарных событий вероятность можно определить различными способами. Выбор вероятностной модели осуществляется на основе дополнительных соображений с привлечением проверки практикой и экспериментом.

30. Частота и классическое определение вероятности. Пусть при проведении N испытаний некоторое событие A появилось m раз.

Отношение mN называется относительной частотой или, для

352

краткости, частотой события A. Многочисленные эксперименты такого рода показывают, что при большом N это отношение остается примерно постоянным. На этом факте основано статистическое определение вероятности, которое заключается в том, что за вероятность принимается постоянная величина, вокруг которой колеблются значения частот события при неограниченном возрастании числа N.

Если число элементарных событий n конечно и они равновозможны, то говорят о классическом определении вероятности.

m	ωk , то за вероятность события A принимается число
Если A = U	ωk , то за вероятность события A принимается число
k=1	P(A) = m .
	P(A) = m .	(1)
	n

Другими словами, вероятность события A равна отношению числа исходов, благоприятствующих появлению события, к числу всех исходов данного эксперимента. Из классического определения вероятности следует, что P( ) = 0 , P(Ω) = 1 и

0 ≤ P(A) ≤ 1.

При решении вероятностных задач постоянно приходится иметь дело с выбором из некоторого множества объектов подмножества элементов с заданными свойствами. Такие задачи выбора называются комбинаторными. Они изучены во введении в математику к первому тому (параграф 3, п. 20 , с. 25 – 35).

Рассмотрим некоторое множество A, содержащее n элементов. Это множество можно упорядочить различными способами. Например,

из множества,	состоящего	из трех элементов A = {a,b,c}, можно
получить 6	различных	упорядоченных	множеств:	A1 = {a,b,c} ,
A2 = {a,c,b},	A3 = {b, a,c} ,	A4 = {b,c, a},	A5 = {c, a,b} ,	A6 = {c,b, a}.

Напомним, что каждое упорядоченное подмножество, состоящее из k элементов, называется размещением из n элементов по k. Через Ank

обозначают число всех таких размещений из n элементов по k элементов, которое можно определить формулой

Ak	=	n!	= n(n −1)(n − 2)...(n − k +1).	(2)

n		(n − k)!

Каждое подмножество из A, содержащее k элементов, называется

сочетанием из n элементов по k элементов. Число всех сочетаний из n

элементов по k элементов обозначается Cnk . Имеет место формула

353

<<< < Предыдущая 23 24 25 26 27 28 29 30 31 32 33 3435 / 4935 36 37 38 39 40 41 42 43 44 45 46 47 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.02.2016218.62 Кб36TEST-Kontrolnaya_po_istorii (1).doc
#
18.02.2016107.52 Кб12TEST-Kontrolnaya_po_istorii (1).doc
#
10.11.20196.55 Mб3Tezisy_chast_1._Avtomatizacija_i_mekhanizacija....docx
#
06.09.2019169.47 Кб5Thatcherism.doc
#
18.07.201945.06 Кб2The Baltic Sea Basin .doc
#
18.02.20163.2 Mб59Tom_2.pdf
#
28.09.2019184.55 Кб2Trebovania.rtf
#
18.02.2016176.64 Кб9trebovania_k_oformleniyu.doc
#
18.02.2016284.67 Кб3Trebovania_k_oformleniyu_otchyota_o_praktike.doc
#
28.09.2019248.83 Кб4Trebovania_k_oformleniyu_otchyota_o_praktike.doc
#
18.02.2016248.32 Кб3trebovania_k_oformleniyu_poyasnitelnoy_zapiski.doc