Tom_2

6.Задана случайная функция X (t) = sin(t + ϕ) , где ϕ – случайная величина, распределенная равномерно в интервале (0;2π ) . Доказать, что X (t) – стационарная функция.

7.Может ли функция KX (τ ) = e−τ (1+ τ +τ 2 ) быть корреляционной функцией стационарной случайной функции X (t) ?

Указание. Проверить выполнение свойств корреляционной функции.

8.Найти спектральную плотность стационарной случайной функции X (t) ,

однородной цепи Маркова. Найти матрицу переходных вероятностей P3 за три шага.

10.В условиях примера 2 найти P1(4) – вероятность полной исправности системы S в результате 4-й проверки.

424

эргодической. Найти стационарное распределение вероятностей p = ( p1, p2 ) .

425

ГЛАВА 12

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА И ПРОВЕРКА ГИПОТЕЗ

§ 1. Основные понятия математической статистики

Введем основные понятия математической статистики: генеральную и выборочную совокупности, вариационный ряд и рассмотрим их простейшие свойства.

10. Генеральная и выборочная совокупности. Основной задачей математической статистики является разработка методов исследования закономерностей массовых явлений и процессов на основании некоторых наблюдений или эксперимента. Другими словами, требуется оценить характеристики генеральной совокупности по выборочным данным.

Под генеральной совокупностью подразумеваем все исходы случайного испытания, всю совокупность значений случайной величины X или всевозможные наблюдения интересующего нас показателя или, в этом случае говорят, параметра. Примером генеральной совокупности могут быть данные о доходах всех жителей республики, партия деталей одного наименования, множество всех рыб в о з е р е и т . д .

Генеральную совокупность можно изучать путем сплошного наблюдения ее объектов. Так поступают, например, в случае переписи населения страны. Однако чаще имеют дело лишь с некоторой частью возможных наблюдений, взятых из генеральной совокупности, т.е. имеют дело с выборочной совокупностью или выборкой. Таким образом, выборка – это множество наблюдений, выбранных из генеральной совокупности. Для иллюстрации введенных понятий рассмотрим следующую задачу.

Предприятие выпустило партию продукции, состоящую из N изделий. Некоторое число изделий из этой партии может иметь дефекты. Осматривать все изделия дорого и трудоемко. Поэтому из всей партии производится выборка из n элементов, и все изделия этой выборки подвергаются проверке. На основании полученных данных требуется сделать вывод о числе дефектных деталей во всей п а р т и и .

Таким образом, задача математической статистики состоит в том, чтобы исследовать свойства выборки и обобщить эти свойства на всю генеральную совокупность.

426

Количество элементов генеральной или выборочной совокупности называют ее объемом. В приведенной выше задаче объем генеральной совокупности равен N, а объем выборки – n элементов.

Выборку следует формировать случайным образом.

Выборка называется случайной, если каждый элемент генеральной совокупности имеет равные шансы попасть в выборку.

Случайные выборки подразделяют на повторные и бесповторные. Выборка называется бесповторной, если каждый отобранный элемент перед выбором следующего обратно в генеральную совокупность не возвращается. Если же после извлечения элемента из генеральной совокупности он фиксируется и возвращается обратно, то это будет повторная выборка.

Целью математической статистики является получение выводов о параметрах, виде распределения и других свойствах случайных величин генеральной совокупности по конкретной выборке. Но всегда в этом случае возникает вопрос: насколько хорошо представляет выборка характеристики генеральной совокупности?

Выборка называется репрезентативной (представительной), если она достаточно полно представляет изучаемые признаки и параметры генеральной совокупности. Понятие “достаточно полно представляет”, безусловно, не является однозначным. В связи с этим заметим, что любая выборка, как правило, не дает точной характеристики всей генеральной совокупности. Но поскольку выборка является случайной, то к ней применимы положения и теоремы теории вероятностей. На основании закона больших чисел можно предполагать, что чем больше объем выборки, тем точнее будет она представлять генеральную совокупность. Требуемая точность представления по тем или иным параметрам и является условием для о п р е д е л е н и я о б ъ е м а в ы б о р к и .

20. Вариационный ряд и его характеристики. Предположим,

что генеральная совокупность описывается случайной величиной X. Тогда выборку можно определить как совокупность

наблюдаемых значений случайной величины X, соответствующих n независимым повторениям экспериментов. Исходы испытаний можно представить в виде табл. 1.

427

Такую таблицу называют простым статистическим рядом.

Он является первичной формой представления статистических данных. Простейшим способом организации данных в выборке является их группировка по возрастанию либо по убыванию. Если

предположить, что

x1 ≤ x2 ≤ ... ≤ xn ,

то последовательность (1) называют вариационным рядом, а члены этой последовательности – вариантами. Разность между максимальным и минимальным элементами называют размахом выборки.

Совокупность (1) может содержать равные между собой члены. Если подсчитать частоты (кратности), с которыми встречаются различные члены в последовательности (1), то можно составить следующую табл. 2.

и обычно их располагают в порядке возрастания.

Данные табл. 2 иногда представляют графически следующим образом. Взяв на плоскости систему координат, на оси абсцисс откладывают варианты, а на оси ординат – частоты. В результате на плоскости получим систему из k точек: (x1′; m1), (x2′ ; m2 ), ... ,(xk′ ; mk ) .

Если соединить эти точки, то получим ломаную линию, которая называется полигоном распределения или частотным полигоном.

Объемом вариационного ряда называют число m1 + m2 + ... + mk .

распределением выборки. Статистическое распределение также записывают в виде таблицы, первая строка которой содержит различные варианты xi′ , а вторая – их относительные частоты wi .

При неограниченном росте числа испытаний относительные частоты wi стремятся к вероятностям pi = P(xi′) значений xi′ , а

428

статистическое распределение выборки переходит в закон распределения дискретной случайной величины X.

Статистической (эмпирической) функцией распределения выборки называется функция Fn (x) , определяющая для всякого x

относительную частоту события { xi < x} , то есть

Эмпирическая (статистическая) функция распределения выборки характеризует в некоторой мере теоретическую функцию распределения генеральной совокупности, т.к. в силу теоремы Бернулли (см. п 10.8.30) Fn (x) → F(x) в вероятностном смысле.

Процедуру обработки данных выборочной совокупности рассмотрим на примере объема продаж телевизоров в универмаге за 10 рабочих дней. Пусть объемы продаж задаются следующей табл. 3.

Данная таблица представляет собой простой статистический ряд. Объем выборки равен 10. Теперь составим вариационный ряд. Он имеет вид: 2, 4, 4, 5, 5, 5, 6, 6, 6, 7.

Размах выборки, очевидно, равен 5. Подсчитав частоты, составим табл. 4:

Таблица 4

429

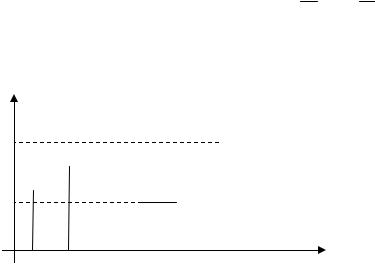
Построим полигон распределения (рис. 1).

Легко строится также график статистической функции распределения (рис. 2).

Рис. 1 Рис. 2

Выше рассматривались дискретные вариационные ряды. Если же число вариант xk′ велико или случайная величина X, описывающая

выборку, является непрерывной, то отдельные значения изучаемой случайной величины объединяют в группы или интервалы, указывая верхнюю и нижнюю границы каждого интервала. В этом случае говорят уже об интервальных вариационных рядах.

В качестве примера рассмотрим отклонения от номинального

Объем выборки N = 40 , ее размах равен 0,14 − 0,02 = 0,12 . В данном случае удобно прибегнуть к интервальному вариационному ряду. Выбор интервалов можно осуществлять исходя из каких-либо практических или иных соображений. Часто с этой целью прибегают к методу Стерджесса. В таком случае число интервалов рассчитывается по формуле

k =1+ 3,322lg N .

430

Интервальный вариационный ряд можно изобразить графически. С этой целью на плоскости строят систему координат и по оси абсцисс откладывают интервалы значений параметра. На основании

интервалов строят прямоугольники с высотой, равной mhi или whi .

Полученная фигура называется гистограммой частот или относительных частот. Для рассматриваемого примера гистограмма относительных частот изображена на рис. 3.

распределения на i-м интервале. Площадь i-го прямоугольника равна

431

mNi , т.е. сумме относительных частот вариант xi′ i-го интервала.

Площадь всей гистограммы относительных частот равна единице. При построении гистограммы, как и при построении полигона, масштаб на осях абсцисс и ординат может быть различным.

§ 2. Числовые характеристики выборки случайной величины и аппроксимация выборочного распределения

Рассмотрим числовые характеристики выборки случайной величины. Изложим метод моментов построения оценки плотности непрерывного распределения.

10. Среднее значение выборки и выборочная статистическая дисперсия. Пусть имеется генеральная совокупность, описываемая случайной величиной X. Обозначим через F(x) закон распределения этой случайной величины. Пусть совокупность (x1, x2 ,..., xn ) – какая-

либо выборка из рассматриваемой генеральной совокупности. Тогда для этой выборки можно построить эмпирическую функцию распределения Fn (x) , по которой можно оценивать функцию F(x).

Для распределения выборки можно вычислить характеристики положения центра группирования, характеристики рассеивания, асимметрию и эксцесс. Эти характеристики будут эмпирическими, полученными из наблюдений. Так как функция Fn (x) является

оценкой функции F(x) генеральной совокупности, то будем считать названные эмпирические характеристики оценками соответствующих характеристик F(x).

Так, средним значением выборки (выборочным средним)

называют число

Величину x можно считать оценкой математического ожидания MX величины X.

Легко видеть, что если xi′ – варианты выборки, mi – их частоты, i =1,k , то

432

Выборочной (статистической) дисперсией случайной величины

X называется число

Очевидно, выборочная (статистическая) дисперсия характеризует меру рассеивания вариант вокруг среднего выборочного.

Легко показать, что

Действительно, по формуле (2’), имеем

Теперь воспользуемся определением величины x и тем, что

и получим

Dn ( X ) = x2 - 2x × x + x2 = x2 - ( x )2 .

Выборочная дисперсия есть средняя величина квадратов отклонений. Чтобы получить характеристику меры разброса случайной величины вокруг выборочного среднего, имеющую ту же размерность, извлекают квадратный корень из дисперсии.

Выборочным средним квадратичным отклонением или выборочным стандартным отклонением случайной величины X называют число

Если рассматриваются интервальные вариационные ряды, то в формулах (1’), (2’) и ниже в качестве значений xi′ , как правило, берут

средние значения параметра на интервалах (xi ; xi+1) .

Пример 1. Данные о валовом сборе зерновых фермерских хозяйств района приведены в табл. 1.

Таблица 1

433