Tom_2

Пример 2. Три товарища независимо друг от друга возвращаются из дачи электричкой, содержащей 8 вагонов. Какова вероятность того, что они окажутся в разных вагонах?

Решение. Согласно классическому определению вероятности,

40. Геометрическая вероятность. В тех случаях, когда пространство элементарных событий Ω содержит бесконечно много элементарных событий, часто возникает понятие геометрической вероятности, которое заключается в следующем.

Под достоверным событием будем понимать некоторую область Ω в n-мерном пространстве. Событиями являются подмножества A Ω , а их вероятности определяются как отношение объемов:

A B , то P(A) ≤ P(B).

Пример 4 (задача о встрече). Два товарища договорились о встрече в промежутке одного часа, причем каждый из них, приходя на встречу, ожидает второго не более 20 минут. Какова вероятность того, что встреча состоится?

354

Условие встречи задается неравенством t1 - t2 < 13 , которое определяет область A, заштрихованную на рисунке 2. Тогда

§2. Теоремы сложения и умножения вероятностей, условная вероятность

Рассмотрим теоремы сложения и умножения, определения независимых событий.

10. Теорема сложения вероятностей. Найдем вероятность суммы событий, используя классическое определение вероятности. Пусть в результате некоторого эксперимента, состоящего из n исходов, событию A благоприятствуют m1 исходов, а событию B – m2 исходов.

Если при этом одновременному появлению событий A и B

Если события A и B несовместны, то из (1) получим теорему сложения вероятностей:

т.е. для несовместных событий вероятность суммы событий равна сумме вероятностей.

Так как A + A = W и A × A = Æ , то P(A + A)= P( A) + P(A) =1 и

Пример 1. Из группы студентов 10 % знают английский язык, 5 % – французский и 1 % – оба языка. Какова вероятность того, что наугад выбранный студент не знает ни одного иностранного языка?

Решение.

P =1- (0,1+ 0,05 - 0,01) = 0,86 . □

20. Условная вероятность. На практике часто возникают ситуации, когда заранее известно, что некоторое событие B произошло. В этом случае B становится

355

достоверным событием, а вероятности всех событий некоторым образом меняются. Тогда говорят об условных вероятностях, P(A B) –

вероятность события A при условии, что B произошло. Пусть имеется всего n исходов, из них m исходов благоприятствуют появлению события B, а k исходов благоприятствуют появлению события A× B

(рис. 1).

Если событие B произошло, то количество всех возможных исходов будет равно m, из них благоприятствующих событию A будет k исходов. Поэтому

k

P(A B)= mk = mn = P( A× B) .

n

Получили формулу для вычисления условных вероятностей:

и мы получаем теорему умножения вероятностей: если события

A и B независимы, то вероятность произведения событий равна произведению их вероятностей.

Отметим, что соотношение (6) можно принять за определение независимости событий A и B.

Пример 2. Среди изделий, выпускаемых заводом, 5 % бракованных, из работоспособных изделий 95 % соответствуют ГОСТу. Какова вероятность того, что наугад взятое изделие будет удовлетворять требованиям ГОСТа?

Решение. Пусть A – событие, заключающееся в том, что изделие удовлетворяет ГОСТу, B – изделие работоспособное. Тогда требуемая вероятность будет равна

356

P( A× B) = P(A B)× P(B) = 0,95(1- 0,05) = 0,9025 . □

Пример 3. При приеме сообщений каждый символ искажается с вероятностью 0,01. Какова вероятность того, что слово из 5 букв будет передано правильно?

Решение. Считая передачи сигналов независимыми событиями, используя теорему умножения вероятностей, получим:

p = (1- 0,01)5 = 0,951. □

§ 3. Испытания Бернулли. Формулы полной вероятности и Байеса

Приведем формулы Бернулли, полной вероятности и Байеса.

10. Формула Бернулли. Пусть производится n независимых испытаний, в каждом из которых возможно событие A с вероятностью

p и A – с вероятностью q, p + q =1. Такие испытания называются испытаниями Бернулли. Если наступает событие A, то говорят, что имеет место успех. Найдем Pn (m) – вероятность m успехов из n

испытаний.

Результат испытаний Бернулли можно представить

последовательностей равно числу способов выбрать m элементов из n элементов, не отличающихся порядком, т.е. числу сочетаний Cnm .

Вероятность появления каждой такой последовательности, ввиду независимости испытаний, равна произведению вероятностей, т.е.

pmqn−m . Так как события ωi несовместны, то по теореме сложения получим, что

Эта формула носит название формулы Бернулли.

Пример 1. Завод выпускает изделия, из которых 5 % являются бракованными. Для проверки взяты 5 изделий. Какова вероятность того, что среди них окажется не менее двух бракованных?

Решение. Будем считать успехом, если изделие бракованное.

Тогда вероятность успеха p = 201 , а q = 1920 . Можно считать, что имеются n = 5 испытаний Бернулли с вероятностью успеха p. Пусть

357

μ – число успехов, а B – событие, состоящее в том, что μ ³ 2 .

20. Наиболее вероятное число успехов. Определим наиболее вероятное число успехов в n испытаниях Бернулли. Для этого

Þ qm + q < pn - pm Þ ( p + q)m < np - q ,

так как p + q =1, то m < np − q .

Значит, при m < np − q указанная функция Pn (m) возрастает, а при m > np − q убывает. Тогда максимум Pn (m) достигается при m, равном

где [np - q] – целая часть числа np − q . Если число np − q – целое, то максимум Pn (m) обеспечивает также число m′ = np - q .

Пример 2. По данным наблюдений, доля солнечных дней в июне составляет 70 %. Найти наиболее вероятное количество солнечных дней.

достоверное событие. В этом случае говорят,

358

что события B1, B2 , K, Bn составляют полную группу событий, а

события называют гипотезами. Эти события разбивают пространство Ω на непересекающиеся множества (рис. 1).

Пусть A произвольное событие. Тогда A можно представить в виде суммы несовместных событий:

A = ( A× B1 ) + ( A× B2 ) +K + ( A× Bn ) .

Согласно теореме сложения, имеем

k=1

Полученная формула называется формулой полной вероятности.

Пример 3. На экзамене студенту предварительно задается один вопрос. Если он правильно ответит, то с вероятностью 0,8 может сдать экзамен, а если нет, то вероятность сдать экзамен равна 0,2. Студент освоил 80 % всех вопросов. Какова вероятность в результате получить положительную оценку?

Решение. Пусть B1 – событие, состоящее в том, что студенту попадется известный ему вопрос, а B2 – неизвестный, A – положительный исход экзамена. События B1 и B2 образуют полную группу событий, так как B1 × B2 = Æ , B1 + B2 = W . По условию задачи

P(B1 ) = 0,8 ; P(B2 ) = 0,2 ; P( A/ B1 ) = 0,8 ; P( A/ B2 ) = 0,2 .

По формуле полной вероятности получим

P( A) = P( A/ B1 ) P(B1 ) + P( A/ B2 ) P(B2 ) = 0,8×0,8 + 0,2 ×0,2 = 0,68 . □

40. Формула Байеса. Рассмотрим ситуацию, когда исход события A зависит от некоторых других событий B1, B2 , K, Bn , составляющих полную группу событий, и событие A произошло.

Возникает вопрос, какое из событий (гипотез) Bi , влекущих

появление события A, более вероятно?

Для определения вероятностей гипотез и решения этой задачи служит формула Байеса – формула апостериорных (послеопытных) вероятностей:

359

i=1

Вычисляя вероятности гипотез Bi , можно определить наиболее вероятную гипотезу. □

Пример 4. Во время боевых действий самолет противника выпускает три помехи для дезинформации системы ПВО. Оператор ПВО отличает самолет от помехи с вероятностью 0,9. Точка на экране была принята за самолет. Что более вероятно: появление самолета или помехи?

Решение. Пусть A – событие, заключающее в себе принятое решение, B1 – появление самолета, B2 – помехи. Тогда

и, по формуле Байеса, P(B1 / A) = P( A/ B(1 )P) (B1 ) , где

P A

P( A) = P( A/ B1 )P(B1 ) + P( A/ B2 )P(B2 ) .

Получим P( A) = 0,9 ×0,25 + 0,1×0,75 = 0,3 ,

что более вероятно появление самолета. □

§ 4. Случайные величины и законы их распределения

Вводится понятие случайной величины; рассматриваются функции распределения и плотности вероятностей; рассматриваются дискретные

360

и непрерывные случайные величины; определяется независимость случайных величин.

10. Случайные величины. Случайной величиной X (ω), ω Ω ,

называется функция, определенная на множестве элементарных событий Ω . Случайная величина является функцией элементарных исходов ω , поэтому говорят, что случайная величина – это величина, значения которой зависят от случая.

Примеры случайных величин.

1.Число грузовых машин, проезжающих за один час через контрольный пост ГАИ.

2.Время ожидания в очереди.

3.Момент отказа технической системы.

4.Число бракованных изделий, выпускаемых предприятием за определенное время.

Совокупность вероятностей

для различных a и b называется распределением случайной величины.

20. Функция распределения. Рассматривая для любого x вероятность события { X (ω) < x} , получим функцию действительной переменной, которая называется функцией распределения:

Функция распределения однозначно задает распределение случайной величины, так как по ней находятся вероятности вида

Этот факт следует из равенства (4).

361

4) Функция распределения непрерывна слева.

Можно показать, что любая действительная функция, удовлетворяющая перечисленным выше свойствам, является функцией распределения некоторой случайной величины.

Пример 1. Предприятие выпускает изделия, среди которых 60 % стандартных. Наугад выбираются 5 изделий. Найти функцию распределения числа стандартных изделий в выборке.

вероятности m успехов (m = 0,5) по формуле Бернулли:

Тогда: при x ≤ 0

F(x) = P{m < x} = 0;

при 0 < x ≤1

F(x) = P{m < x} = P{m = 0} = 0,01024;

при 1 < x ≤ 2

F (x) = P{m < x} = P{m = 0, m =1} = P5 (0) + P5 (1) = 0,08704 ;

при 2 < x ≤ 3

F (x) = P{m = 0, m =1, m = 2} = 0,08704 + P5 (2) = 0,31744 ;

при 3 < x ≤ 4

F (x) = P{m < x} = P{m = 0,1,2,3} = 0,31744 + P5 (3) = 0,66304 ;

при 4 < x ≤ 5

F (x) = P{m < x} = P{m = 0,1,2,3,4} = 0,66304 + P5 (4) = 0,92224 ;

при x > 5

F (x) = P{m < x} = P{m = 0,1,2,3,4,5} = 0,92224 + 0,07776 =1.

График функции F(x) имеет вид, изображенный на рис. 1:

362

F(x)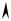

1

Рис.1 □

Пример 2. Функция распределения случайной величины X есть FX (x) . Найти функцию распределения случайной величины Y = a + σX ,

σ > 0 .

Решение.

30. Дискретные случайные величины. Случайная величина X

называется дискретной, если она принимает конечное или счетное множество значений xi , i =1, 2, K Распределение дискретной случайной

где å pi =1.

i

Если число значений X конечно и равно n, то распределение X задается таблицей, называемой также рядом распределения:

типичный пример функции распределения дискретной случайной в е л и ч и н ы .

40. Непрерывные случайные величины. Случайная величина называется непрерывной, если ее функция распределения F(x)

непрерывна. Для непрерывной случайной величины X вероятность того, что она примет конкретное числовое значение, равна нулю.

Действительно,

{ X = x0} Ì {x0 £ X < x0 + Dx} ,

363