Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гродненский государственный университет им. Я. Купалы

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Tom_2

.pdf

Скачиваний:

Добавлен:

18.02.2016

Размер:

3.2 Mб

Скачать

☆

<<< < Предыдущая 18 19 20 21 22 23 24 25 26 27 28 2930 / 4930 31 32 33 34 35 36 37 38 39 40 41 42 > Следующая >>>

¶um,n

¶2um,n

¶3um,n

êum,n + h

¶x

¶x2

¶x3

¶4um,n

h5 ¶5um,n

¶6um,n

- 2um,n +

4! ¶x4

5! ¶x5

¶x6

+um,n - h

¶um,n

h2 ¶2um,n

h3 ¶3um,n

h4 ¶4um,n

¶x

2! ¶x2

¶x3

¶x4

¶5u

m,n

¶6u

m,n

¶u

m,n

êum,n + μh2

5! ¶x5

6! ¶x6

μh2 ë

¶t

+ μ

um, n

+ O(h6 ) =

- um, n ú

¶t2

¶t3

= a2

¶2um, n

¶um, n

h2 æ

¶4um, n

- μ

¶2um, n ö

¶x2

¶t

¶x4

¶t2 ÷

um,n

(

6 )

+ O

360

¶x6

¶t3

Разность

L(u) -

(u) = R(u)

(7)

называется ошибкой аппроксимации, происшедшей от замены дифференциального уравнения конечно-разностным.

Дифференцируя уравнение (4), получаем соотношения

a	2 ¶4u	=	¶2u		, a	2	¶6u	=	¶3u	,
	¶x4		¶t	2			¶x6		¶t3

подставляя которые в тейлорово разложение величины L(u) находим новую форму записи:

¶4um, n

μ2

ö ¶6um, n

L (u) =

- μ

+ h4

+ O

¶x

360

¶x

Подберем

теперь

число

так,

чтобы

(u)

содержащий h2 , т.е. положим

- μ = 0,

μ =

1 .

Теперь, при выбранном μ ,

имеем

(h6 ) .

исчез член,

(8)

294

(u) = -

¶6um,n

+ O (h6 ) .

(9)

¶x6

540

Подставив найденное значение μ =

в равенство (6), получим

основную вычислительную формулу

n+1

éa2u

m+1, n

+ 2(3 - a2 )u

m, n

+ a2u

(10)

m−1, n û

порядок точности которой определяется величиной O(h4 ) . С помощью формулы (10) и решается основная задача. Значения u(x,t) , входящие в правую часть формулы (10), сперва вычисляются для строки (слоя),

где t = 0 , что	возможно сделать, зная начальные условия
u(xm ,0) = f (xm )	(m = 1,2,...). Для узлов последующих слоев значения

функции вычисляются по формуле (10), кроме крайне левого и крайне

правого узлов каждого слоя,	в которых значения u(x,t) могут быть
вычислены на основании	граничных условий: u(0,tn ) = ϕ(tn ) ,
u(l,tn ) =ψ (tn ) .

Предположим теперь, что в начале вычислений в точках нулевого

слоя допущена некоторая погрешность εm,0 :
u(xm ,0) = f (xm ) + εm,0	(11)

и проследим влияние этой погрешности на процесс вычислений, на его устойчивость.

Пусть v(xm ,tn ) –			решение уравнения (6) при условии, что в
точках начального слоя допущена погрешность (11), т.е.
μa2v	m+1,n	+ (1	- 2a2μ )v	+ a2μv	- v	= 0 ,	(12)
	m+1,n		m,n	m−1,n	m,n+1

причем v(xm ,0) = f (xm ) + εm,0 , v(0,tn ) = ϕ(tn ) , v(l,tn ) =ψ (tn ) .

Обозначим разность v(xm ,tn ) - u(xm ,tn ) = w(xm ,tn ) . Вычитая почленно из уравнения (12) уравнение (6), находим:

μa2w	+ (1- 2a2μ )w	+ a2μw	- w	= 0 ,	(13)
m+1,n	m,n	m−1,n	m,n+1
w(xm ,0) = v(xm ,0) - u(xm ,0) = εm,0 ,
	w(0,tn ) = v(0,tn ) - u(0,tn ) = 0 ,
	w(l,tn ) = v(l,tn ) - u(l,tn ) = 0 .
Решение уравнения (13), удовлетворяющее условиям
	w(0,tn ) = 0,	w(l,tn ) = 0 ,			(14)

будем искать в форме

295

= λtn sin px

( p > 0) .

(15)

m,n

На

основании

условий

(14)

имеем:

λtn

= sin p × 0 = 0,

λtn sin pl = 0 ,

можем

вычислить

число

pl = kπ ,

p =

kπ

(k = 1,2,...) , и функцию

kπ

= λtn

sin

(16)

m,n

Найденное решение подставим в уравнение (13)

μa2λtn sin

kπ

+ h) + (1- 2a2μ)λtn sin

kπ

+a2μλtn sin

- h) - λtn +τ sin

= 0

и вычислим множитель λ :

μa2λtn

ésin kπ (x

+ h) - 2sin kπ x

+ sin kπ (x - h)ù

+λ

tn (

- λ

)

kπ

= 0,

sin

μa2λtn é2sin kπ x

cos kπ h - 2sin kπ x

+λtn (1- λτ )sin kπ x

m ú

= λtn sin

kπ

éμa2 æ

2cos

kπ

h - 2

+ (1- λτ )ù

= λtn sin

kπ

-4μa2 sin

kπ

= 0 ;

´ê

h + (1- λτ )ú

kπ

1- λτ - 4μa2 sin2

λ =

4μa2 sin2

h = 0,

ç1

h÷

Таким образом, получено множество частных решений

уравнения (13):

kπ

wk (xm ,tn ) =

ç1- 4μa2 sin2

sin

xm .

Из теории конечно-разностных уравнений известно, что линейная

комбинация этих решений есть также решение уравнения (13)

N −1

N−1

kπ

w(xm ,tn ) =

å Ck wk (xm ,tn ) =

å Ck ç1- 4μa2 sin2

h÷

sin

xm .

k=1

296

Коэффициенты Cm подбираются так,

чтобы

выполнялось

условие w(xm ,θ ) = εm,0 .

Конечно-разностная схема будет устойчивой, если при любых Cm

функция w(xm ,tn ) останется ограниченной при

t → ∞ ;

а для этого

достаточно, чтобы при всех k выполнялось неравенство

kπ

≤ 1,

1− 4μa2 sin2

или

kπ

1 ;

0 ≤ μa2 ≤ 1 ,

0 ≤ μa

2 sin2

h ≤

0 < μ ≤

(17)

2a2

Неравенство (17) определяет достаточное условие устойчивости.

Пример 2. Найти для x = 0, 2m ,

m = 0,1,...,5 , t = 0,08 решение

уравнения

∂u

∂2u

, 0 ≤ x ≤ 1,

0 ≤ t ≤ 0,08 ,

удовлетворяющее

∂t

∂x2

условиям u(0,t) = t ,

u(1,t) = 0,5 + t ,

0 ≤ t ≤

0,08 ,

u(x,0) =

0 ≤ x ≤ 1 , взяв h = 0,2 , τ = 0,02 .

Решение.

Конечно-разностная

форма

уравнения

теплопроводности имеет вид (6). Для данного уравнения

теплопроводности имеем a = 1, μ =	τ	=	0,02	=	1	. Таким образом из
	h2		0,04		2

(6) и заданных условий, разностная схема для нашей задачи запишется в виде

	u	m,n+1	=	1	(u	m−1,n	+ u		m+1,n	) , u		= t	n	,	u	= 0,5 + t		n	, u	m,0	=	x2	,
	u		=		(u		+ u			) , u		= t		,	u	= 0,5 + t			, u		=		,
				2							0,n				5,n						2
m = 1,2,3,4,5 ,					n = 0,1,2,3 . Результаты вычислений приведем в таблице 1.
																			Таблица 1

		n			u0,n			u1,n			u2,n				u3,n		u4,n			u5,n
		0			0,00			0,02			0,08				0,18		0,32			0,50
		1			0,02			0,04			0,10				0,20		0,34			0,52
		2			0,04			0,06			0,12				0,22		0,36			0,54
		3			0,06			0,08			0,14				0,24		0,38			0,56				□
		4			0,08			0,10			0,16				0,26		0,40			0,58				□

297

40. Уравнение Лапласа в конечных разностях. Задача Дирихле.

Представим уравнение Лапласа

(m-1;n+1) (m+1;n+1)

(m;n)

(m-1;n-1) (m+1;n-1)

Рис. 1

¶2u + ¶2u = 0 ¶x2 ¶y2

в конечных разностях. Выберем систему узлов (m;n) , (m +1;n +1) , (m −1;n +1) ,

(m −1;n −1) , (m +1;n −1) квадратной сетки

(рис. 1) и выразим правую часть уравнения Лапласа через значение функции u = u(x, y)

в выбранных узлах. Пусть h – шаг сетки. Воспользовавшись формулой Тейлора для функции двух переменных, найдем разности функций:

um+1,

um−1,

um+1,

æ ¶um, n

¶um, n ö

¶2um, n

2¶

2um, n

¶2um, n

n+1 - um, n = h

è ¶x

¶y ø

¶x

¶x¶y

¶y

+ h

um, n

+ O(h4

+ 3

¶x

¶y

¶x¶y

¶y

¶um, n

¶um, n ö

¶2um, n

n+1 - um, n = hç

- 2

¶x

¶x¶y

¶y

¶y ø 2! è

um, n

+ h

ç -

um, n

- 3

um, n

+ O(h4 ),

¶y3

¶x3

¶x2¶y

¶x¶y2

¶um, n

¶um, n ö

¶2um, n

n−1 - um, n = hç

+ 2

¶x

¶y ø 2!

¶x

¶x¶y

¶y

um, n

+ h

ç -

- 3

+ O(h4 ),

¶y3

¶x3

¶x2¶y

¶x¶y2

æ ¶um, n

¶um, n ö

h2 æ

2um, n

¶2um, n

n−1

- u

= h

m, n

¶x

¶y

¶x

¶x¶y

¶y

2! è

um, n

+ O(h4

- 3

+ 3

¶x

¶y

¶x¶y

¶y

298

Сложив полученные разложения, вычислим конечно-разностную форму уравнения Лапласа:

+ u

= 2h

¶2u

¶2u ö

+ O

(

)

m+1, n+1

m−1, n+1

m−1, n−1

m+1, n−1

m, n

¶x

¶y

¶2u

+ ¶2u

= éu

m+1, n+1

+ u

m−1, n+1

+ u

m−1, n−1

+ u

m+1, n−1

- 4u

+ O

(

)

= 0,

¶x

¶y

m, n û

откуда следует разностное уравнение

m,n

1 éu

m+1, n+1

+ u

m−1, n+1

+ u

m−1, n−1

+ u

ù .

(18)

m+1, n−1 û

узлов (m;n) ,

(m +1;n) ,

(m;n +1) ,

(m −1;n) ,

Избрав систему

(m;n −1)

(рис.

2) и выполнив вычисления, аналогичные только что

изложенным, получим иную конечно-разностную форму уравнения Лапласа:

¶2u +

¶2u

éu

m+1, n

+ u

m, n+1

+ u

m−1, n

+ u

m, n−1

- 4u

m,n

ù + O(h2 ) = 0 .

¶x

¶y

2 ë

Пренебрегая величиной O(h2 ) , будем иметь разностное уравнение

m,n

= 1 éu

+ u

m, n+1

+ u

m−1, n

+ u

m, n−1

ù .

(19)

m+1, n

Возможны

иные,

чем нами

(m;n+1)

рассмотренные, системы узлов и,

следовательно, иные конечно-разностные

(m;n)

представления уравнения Лапласа.

Рассмотрим

теперь

применение

(m-1;n)

(m+1;n)

метода сеток к решению внутренней

задачи Дирихле для уравнения Лапласа.

(m;n-1)

Пусть

надо

вычислить функцию

Рис. 2

u = u(x, y) ,

удовлетворяющую в некоторой

конечной области D уравнению

¶2u

= 0 , а на границе Г области D

¶x2

¶y2

условию

uГ = f (x, y) ,

(20)

где f (x, y) – заданная, непрерывная на границе Г функция.

Для конечно-разностной аппроксимации заданного уравнения можно воспользоваться одной из формул (18) или (19). Все те узлы, лежащие в области D, для которых можно написать то или иное конечно-разностное соотношение, называются внутренними узлами сеточной области. На рис. 3 они отмечены кружками. Для узлов,

299

Рис. 3

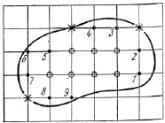
отмеченных цифрами и звездочками, конечно-разностные соотношения написать невозможно. Эти последние узлы называются граничными узлами сеточной области. Для узлов, лежащих на границе Г (они отмечены звездочками (рис. 3)), значения функции u(x, y) могут быть

определены из граничных условий. Для вычисления значения функции в узлах, отмеченных цифрами, может быть рекомендована специальная

методика. Так, например, если область D имеет криволинейную границу Г, то значения um,n для граничных узлов можно найти путем

переноса значений u(x, y) из точек на границе Г. Погрешность аппроксимации условия (20) в узле (xm ; yn ) будет величиной O(δ ) ,

где δ – расстояние от этого узла до точки на границе Г, с которой переносится значение функции.

Погрешность аппроксимации граничного условия можно


уменьшить, если		для определения um,n				в граничном узле
воспользоваться значением u(x, y)					в некоторой точке границы Г и в
близком внутреннем узле.
Пример 3. Найти решение уравнения
∂2u(x, y)	+	∂2u(x, y)		= 0,	0 ≤ x ≤ 0,8,	0 ≤ y ≤ 0,8 ,
∂x2		∂y2

удовлетворяющее граничным условиям
u(x,0) = x2 ,			u(x;0,8) = x2 − 0,64, 0 ≤ x ≤ 0,8
u(0, y) = −y2 ,			u(0,8; y) = 0,64 − y2 ,			0 ≤ y ≤ 0,8,

на сетке (xm ; yn ), xm = 0,2m, yn = 0,2n, m, n = 0,1,2,3,4.

Решение. Для конечно-разностной аппроксимации заданного уравнения воспользуемся формулой (19).

Так как область D является прямоугольником, то поставленная граничная задача будет аппроксимироваться следующей системой алгебраических уравнений

um,n−1 + um−1,n − 4um,n + um+1,n + um,n+1 = 0, m,n = 1,2,3,

um,0 = xm2 , um,4 = xm2 − 0,64, m = 0,1,2,3,4, u0,n = − yn2 , u4,n = 0,64 − yn2 , n = 0,1,2,3,4.

300

Эту систему перепишем в виде

m−1,1

- 4u

m,1

+ u

m,2

+ u

m+1,1

= -x2

um−1,2 + um,1 - 4um,2 + um,3 + um+1,2

= 0,

m−1,3

+ u

m,2

- 4u

m,3

+ u

m+1,3

= 0,64 - x2 ,

m = 1,2,3,

0,1

= -y2 , u

0,2

= -y2 , u

0,3

= -y2 ,

4,1

= 0,64 - y

2 , u

4,2

= 0,64 - y2 , u

4,3

= 0,64 - y2 .

Введем обозначения

æ um,1

æ -4 1 0 ö

-x2

-4

= çum,2

÷, A =

÷, Fm = ç

-4

0,64 - x2

m,3

m ø

-y2

-0,04ö

0,64 - y2

0,60ö

Ф0 =

-0,16

, Ф1

= ç

0,48

-y2

= ç

0,64 - y2

= ç

÷. .

-y2

-0,36

0,64 - y2

0,28

С учетом введенных обозначений система принимает вид

U0 + AU1 +U2 = F1,

U1 + AU2 +U3 = F2 ,

U2 + AU3 +U4 = F3 ,

U0 = Ф0 , U4 = Ф1.

Для ее решения применим метод исключения.

Умножив второе уравнение слева на −A , а затем сложив полученное выражение с первым и третьим уравнениями, найдем

U0 + (2E - A2 )U2 +U4 = F1 - AF2 + F3.

Отсюда

(A2 - 2E)U			2	= T, T = Ф + Ф - F + AF - F ,
			2				0			1	1		2	3
				æ	-15 -8		1 ö					æ	1,6	ö
A	2			ç	-8	16	-8	÷	,		T =	ç	0,64	÷
A		- 2E = ç			-8	16	-8	÷	,		T =	ç	0,64	÷.
				ç	1	-8	15	÷				ç	-2,88	÷
				è	1	-8	15	ø				è	-2,88	ø

Таким образом, для определения		величин u2,n (n = 1,2,3)
требуется решить систему
15u2,1 − 8u2,2 + u2,3	= 1,6,
-8u2,1 +16u2,2 - 8u2,3		= 0,64,
u2,1 - 8u2,2 +15u2,3	= -2,88.

301

Умножив второе уравнение на 2, а затем сложив полученное выражение с первым и третьим уравнениями, найдем u2,2 = 0 . Из

15u2,1 + u2,3

= 1,6,

-u2,1 - u2,3 = 0,08

0,12 ö

имеем u2,1

= 0,12 , u2,3 = -0,20 . Значит,

U2 = ç

÷ .

è -0,20

Найдем U1,U3 . Для этого воспользуемся равенствами

AU1 = T1, T1 = F1 -U0 -U2 ,

AU3 = T3 , T3 = F3 -U2 -U4 ,

æ -0,12ö

æ -1,08ö

T =

0,16

÷,

-0,48

÷.

1,16

0,20

Для вычисления U1 решаем систему

-4u1,1 + u1,2 = -0,12,

u1,1 - 4u1,2 + u1,3 = 0,16, u1,2 - 4u1,3 = 1,16.

Умножив второе уравнение на 4 и сложив полученное равенство с первым и третьим уравнениями, найдем u1,2 = -0,12 . Из первого и

третьего уравнений найдем u1,1 = 0, u1,3 = -0,32 .

	Аналогично	из системы			AU3 = T3				имеем u3,1 = 0,32 ,
u3,2 = 0,20 , u3,3 = 0 .		□
	Задания для самостоятельной работы
1.	Проверить, является ли функция				exp(x2 + y2 )(ϕ(x) +ψ (y)) , где
	ϕ(x),ψ ( y) – произвольные дважды дифференцируемые функции,
	общим решением уравнения		¶2u	- y		¶u	- x	¶u	+ xyu = 0 .
			¶x¶y			¶x		¶y

2.	Найти общее решение уравнений:

302

а)

¶2u

= x + 2y ;

б)

¶2u

= x2 + y2 ;

в)

¶2u

= x2 + y - xy .

¶x2

¶x¶y

3. Привести к каноническому виду уравнения

а)

¶2u

= 0 ;

¶x2

¶x¶y

¶y

б)

¶2u

+ 3

¶u

- 2

¶u

+ 4

= 0 ;

¶x2

¶x¶y

¶y2

¶x

¶y

в) (1+ x2 ) ¶2u + (1+ y2 )¶2u

+ x

¶u

+ y

¶u

= 0 ;

¶x2

¶y2

¶x

¶y

г) x

2 ¶2u

+ 2xy

¶2u

+ y

2 ¶2u

= 0 ;

¶x2

¶x¶y

¶y

д)

¶2u

- 4

¶2u

- 2

¶u

+ 6

¶u

= 0 ; е)

¶2u

= 0 .

¶x2

¶x¶y

¶y2

¶x

¶y

¶x2

¶y2

4.Используя уравнение малых колебаний струны, поставить задачу о вынужденных колебаниях закрепленной на концах x = 0 и x = l горизонтальной однородной струны, если в момент времени t = 0 струна имела форму ϕ(x) , 0 ≤ x ≤ l и скорость струны в каждой ее точке задается функцией ψ (x) . (Указание. Неизвестная функция

u(x,t) , определенная при		0 ≤ x ≤ l		и		0 ≤ t ≤ +∞ , будет являться
решением уравнения	¶2u	= a	2 ¶2u	+	1	F(x,t) , где	a	2	=	T	; T –
	¶t2		¶x2		ρ					ρ

напряжение струны, ρ –		плотность струны, F(x,t)					–		плотность
распределения внешних сил).

5. Используя уравнение малых колебаний струны, поставить задачу о свободных колебаниях закрепленной на конце x = l горизонтальной однородной струны, левый конец которой (при x = 0 ) движется так, что касательная в этом конце (при x → +0 ) в любой момент времени горизонтальна. В момент времени t = 0 струна имела форму ϕ(x) , а скорость каждой точки равна нулю.

(Указание. Функция u(x,t) удовлетворяет уравнению ¶2u = a2 ¶2u ).

¶t2 ¶x2

6.Поставить задачу о распределении температуры внутри однородного изотропного стержня, начальная температура которого равна u0 ,

303

<<< < Предыдущая 18 19 20 21 22 23 24 25 26 27 28 2930 / 4930 31 32 33 34 35 36 37 38 39 40 41 42 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.02.2016218.62 Кб36TEST-Kontrolnaya_po_istorii (1).doc
#
18.02.2016107.52 Кб12TEST-Kontrolnaya_po_istorii (1).doc
#
10.11.20196.55 Mб3Tezisy_chast_1._Avtomatizacija_i_mekhanizacija....docx
#
06.09.2019169.47 Кб5Thatcherism.doc
#
18.07.201945.06 Кб2The Baltic Sea Basin .doc
#
18.02.20163.2 Mб59Tom_2.pdf
#
28.09.2019184.55 Кб2Trebovania.rtf
#
18.02.2016176.64 Кб9trebovania_k_oformleniyu.doc
#
18.02.2016284.67 Кб3Trebovania_k_oformleniyu_otchyota_o_praktike.doc
#
28.09.2019248.83 Кб4Trebovania_k_oformleniyu_otchyota_o_praktike.doc
#
18.02.2016248.32 Кб3trebovania_k_oformleniyu_poyasnitelnoy_zapiski.doc