18. Квадратурные формулы Гаусса

Опр. Говорят, что квадратурная формула

(1)

имеет алгебраическую степень точности m, если она является точной для любого многочлена степени m и существует многочлен степени , для которого квадратурная формула не является точной.

Квадратурные формулы наивысшей алгебраической степени точности называют квадратурными формулами Гаусса (при этом n считается фиксированным). Квадратурное правило имеет алгебраическую степень точности не ниже n тогда и только тогда, когда оно является интерполяционным. Следовательно, коэффициенты квадратурных правил Гаусса определяются формулой

. (2)

Таким образом, остается найти оптимальный набор узлов, при котором интерполяционная квадратурная формула будет иметь наивысшую алгебраическую степень точности. Последняя, как будет доказано, равна .

Лемма 1. Если квадратурное правило (1) имеет алгебраическую степень точности , то многочленстепени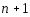ортогонален с весомна отрезкелюбому многочлену меньшей степени.

Д-во. Так как квадратурное правило (1) является точным для любого многочлена степени и,то приимеем, что док-ет лемму.

Из леммы 1 следует, что для построения квадратурного правила алгебраической степени точности необходимо найти многочлен степени, который был бы ортогонален любому многочлену меньшей степени.

Лемма 2. Если почти всюду на, то приведенный многочлен степени, ортогональный нас весомлюбому многочлену меньшей степени, существует и является единственным. При этом все его корни простые и находятся на отрезке.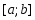

Д-во. Для искомого приведенного многочлена степениусловия ортогональности любому многочлену меньшей степени дают систему линейных алгебраических уравнений(3)

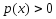относительно неизвестных коэффициентов . Системе (3) соответствует однородная система(4). Уравнения системы (4) умножим на соответствующие коэффициенты и сложим. Из полученного при этом выраженияи условия леммывытекает, что, т.е.. Поскольку однородная система (4) имеет только тривиальное решение, то соответствующая неоднородная система (3) имеет единственное решение.

Пусть - корни нечетной кратности многочлена, лежащие на отрезке. Требуется доказать, что. Допустим противное:. Тогда, в силу ортогональности, выполняется. С другой стороны, так какипочти всюду наимеем. Полученное противоречие доказывает, что. Лемма доказана.

Лемма 3. Если узлами интерполяционной квадратурной формулы (1) являются нули ортогонального многочлена , то квадратурная формула точна для любого мн-на степени.

Д-во. Пусть - произвольный многочлен степени. Представим его в виде,гдеи-многочлены степениn. Имеем

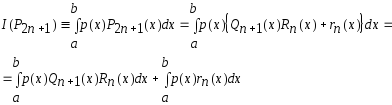Здесь в силу ортогональностии, так как квадратурное правило интерполяционное, то

. Лемма доказана.

Теорема. Если 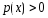почти всюду на, то существует квадратурное правило (1) наивысшей алгебраической степени точности.

Д-во. Существование квадратурного правила (1) алгебр-кой степени точности 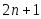непосредственно следует из доказанных лемм. Остается доказать, что нельзя построить квадратурное правило (1), точное для любого многочлена степени. Для многочленастепениимеем значение интегралаи значение квадратурной суммы

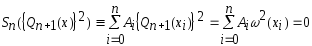.Т-ма док-на.

19. Квадр-ные формулы Гаусса с постоянной весовой ф-ей. Рассмотрим интеграл , (1) где- достаточно гладкая функция. Любой конечный отрезок интегрированиялинейным преобразованием приводится к отрезку. Поскольку в данном случае весовая функция, то квадратурное правило наивысшей алгебраической степени точности (2) существует. Его узлами явл-ся корни мн-на , ортогонального мн-нам меньшей степени с весом 1 на отрезке [-1;1].

_{Обозначим} . Очевидно, и. Возьмем произвольный многочленстепени. Используя условия ортогональности и проводя интегрирование по частям, получим

.

Продолжая процесс интегрирования по частям получим

Отсюда для 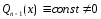, следует, что. Используя произвольность многочлена, последовательно получаем далее.

Таким образом, многочлен степени, производные которого определяются формулойимеет корни, каждый кратностиn. Следовательно, этот многочлен представляется в виде . Для искомого ортогонального многочлена в результате

получим выражение . (3)

Ортогональные многочлены, определяемые формулой (3) называют многочленами Лежандра. В случае выбора константы по правилу будут получаться приведенные многочлены. В практике вычислений для многочленов Лежандра используется формула Родрига.(4)

При этом получается квадрат нормы и рекуррентная формула.(5)

По формуле (3) находим . По формуле (4) находим. Отсюда определяем последовательно

и . Построим несколько квадратурных формул Гаусса вида (2).

При из уравненияполучаем один корень,и один коэффициент. Приходим к квадратурной формуле, имеющей наивысшую алгебраическую степень точности 1.

При из уравненияполучаем два корня,и два коэффициентаи. Приходим к квадратурной формуле, имеющей наивысшую алгебр-скую степень точности 3.

Формула для вычисления коэффициентов квадратурной формулы (2) может быть преобразована к виду(6)

При из уравненияполучаем три корняи три коэффициентаи. Приходим к квадратурной формуле, имеющей наивысшую алгебраическую степень точности 5.