
- •1.Источники и классификация погрешностей. Неустранимая и вычислительная погрешность.
- •2. Постановка задачи интерполирования. Существование и единственность обобщенного интерполяционного многочлена.
- •3. Интерполяционный многочлен Лагранжа.
- •4. Схема Эйткина
- •5. Остаточный член интерполяционного многочлена Лагранжа.
- •6. Минимиз. Оценки остаточного члена интерпол. Мн-на.
- •7. Разделенные разности и интерполяционная формула Ньютона с разделенными разностями.
- •8. Конечные разности и интерполяционные формулы Ньютона с конечными разностями.
- •9. Составление таблиц.
- •10. Сходимость интерполяционного процесса
- •11.Общая задача интерполирования алгебраическими многочленами. Интерполяционный многочлен Эрмита с узлами кратности 2.
- •13 . Оптимизация шага при численном диф-нии
- •14. Интерполяционные квадратурные формулы
- •15. Квадратурные формулы Ньютона-Котеса
- •16. Простейшие квадрат ф-лы н-Кот. И оценка их погрешности.
- •17. Составные квадратурные формулы средних прямоугольников, трапеций, парабол и оценка их погрешности
- •18. Квадратурные формулы Гаусса
- •20. Метод наименьших квадратов.
- •22.Обобщённые мног-ны наилучших среднеквадратических приближений.
- •24. Многочлены наилучших равномерных приближений. Примеры.
- •25. Наилучшие приближения в линейном нормированном пространстве.
- •26. Интерполяционные сплайны.
- •27. Существование и единственность кубического сплайна.
- •28.Краткие сведения о нормах векторов и матриц.
- •29. Обусловленность линейных алгебраических систем.
- •30. Метод Гаусса решения системы линейных ур-ний.
- •31. - Разложение квадратных матриц.
- •32. Разложение симметричных матриц. Метод квадр. Корней решения лин. Алг.Систем
- •34. Принцип сжимающих отображений в метрическом пространстве.
- •35. Метод простой итерации решения лин. Алг. Систем и усл. Его сходимости.
- •36. Метод Якоби решения линейных алгебраических систем
- •37. Метод Зейделя решения лин. Алг. Систем.
- •38. Метод покоординатного спуска решения линейных алгебраических систем.
- •39. Метод скорейшего спуска решения линейных алгебраических систем
- •40. Степенной метод решения частичной проблемы собственных значений.
- •41. Метод Данилевского раскрытия характеристического уравнения
- •42. Метод вращений решения полной проблемы собственных значений.
- •43. Метод бисекции и простой итерации решения уравнений с одним неизвестным.
- •44. Методы хорд и касательных как частные случаи метода простой итерации.
- •45. Методы локализации корней алгебраического уравнения.
- •46. Метод Лобачевского решения алгебраических уравнений.
- •47. Методы простой итерации и Зейделя решения системы нелинейных уравнений.
- •48. Метод Ньютона и аналоги метода Зейделя решения системы нелинейных уравнений.
- •49. Классификация численных методов решения задачи Коши. Методы Эйлера, трапеций и к-э.
- •50. Метод Рунге-Кутта решения задачи Коши. Построение методов р-к второго порядка точности.
- •51. Оценка погрешности и сходимость одношаговых методов решения задачи Коши.
- •52. Экстраполяц. Метод Адамса решения задачи Коши.
- •53. Интерполяционный метод Адамса решения задачи Коши.
- •54. Общий вид линейных многошаговых методов решения задачи Коши.
- •55. Условие корней многошаговых методов решения задачи Коши
- •56. Сходимость многошаговых методов решения Коши.
- •57. Сеточные методы решения краевых задач для обыкновенных дифференциальных уравнений.
- •58. Сходимость сеточного метода решения краевых задач для обыкновенных диф. Уравнений.
- •59. Методы прогонки и пристрелки решения разностных схем при решении краевых задач для обыкновенных д.У.
- •60. Эквивалентность граничных и вариационных задач
- •61. Метод Ритца решения вариационных задач.
- •62. Построение системы линейных уравнений для определения значений параметров в методе Ритца.
- •63. Вариационно-разностный вариант метода Рица.
- •64. Сеточные методы решения краевой задачи для уравнения Пуассона. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •Постpоение pазностной схемы
- •65. Основные понятия теории разностных схем.
- •66. Сходимость сеточного метода
- •Фоpмулиpовка исходной дифференциальной краевой задачи
- •67.Метод матричной прогонки решения разностной схемы. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •68. Разностные схемы для одномерного параболического уравнения. Фоpмулиpовка исходной диффеpенциальной задачи
- •69. Разностные схемы решения задачи Коши для уравнения гиперболического типа.
- •70. Сеточные методы решения смешанной задачи для уравнений гиперболического типа.
- •71. Метод квадратур решения интегрального уравнения Фредгольма 2-го рода.
- •72. Решение интегрального уравнения Фредгольма 2-го рода с вырожденным ядром.
- •Решение интегр. Ур-ния с вырожденным ядром.
- •73. Решение интегрального уравнения Фредгольма 2-го рода методом вырожденного ядра.
- •Способы приближения невырожденного ядра вырожденным.
72. Решение интегрального уравнения Фредгольма 2-го рода с вырожденным ядром.
Интегральное
уравнение Фредгольма 2-го рода имеет
вид:
 . (1)
. (1)
 –заданная функция,
кот. наз. ядром интегр. ур-ния;
–заданная функция,
кот. наз. ядром интегр. ур-ния;
 - заданная функция, кот. наз.свободным
членом или правой частью интегp. ур-ния;
- заданное число, паpаметp интегp. уp-ния;
- заданная функция, кот. наз.свободным
членом или правой частью интегp. ур-ния;
- заданное число, паpаметp интегp. уp-ния;
 -
искомая функция, подлежащая опpеделению.
Однородное интегр. ур-ние Фредгольма
2-го рода
-
искомая функция, подлежащая опpеделению.
Однородное интегр. ур-ние Фредгольма
2-го рода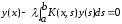 , (2)
всегда имеет тривиальное решение
, (2)
всегда имеет тривиальное решение .
Значения
.
Значения ,
при кот. однородное ур-ние (2) имеет
нетривиальные решения, наз. собственными
значениями ядра
,
при кот. однородное ур-ние (2) имеет
нетривиальные решения, наз. собственными
значениями ядра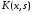 ,
а сами нетривиальные решения –
собственными функциями ядра. Для интегр.
ур-ния Фредгольма 2-го рода возможны две
альтернативы:1)неоднор. интегр. ур-ние
Фредгольма (1) имеет единственное решение
при любых правых частях; 2) соответствующее
однор. ур-ние (2) имеет нетривиальные
решения. Ядpо
,
а сами нетривиальные решения –
собственными функциями ядра. Для интегр.
ур-ния Фредгольма 2-го рода возможны две
альтернативы:1)неоднор. интегр. ур-ние
Фредгольма (1) имеет единственное решение
при любых правых частях; 2) соответствующее
однор. ур-ние (2) имеет нетривиальные
решения. Ядpо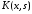 называется выpожденным, если оно
пpедставляется в виде:
называется выpожденным, если оно
пpедставляется в виде: (3) функции
(3) функции можно считать линейно независимыми.
можно считать линейно независимыми.
Решение интегр. Ур-ния с вырожденным ядром.
В случае выpожденного
ядpа pешение интегp. уp-ния можно пpедставить
в виде линейной комбинации функций
 :
: (4).
Подставим в интегр. ур-ние (1) ядро в виде
(3): , (5) вынесем знак суммы за знак
интегpала и оставим в левой части только
y(x), тогда получим (4) и следующее выpажение
для коэффициентов:
(4).
Подставим в интегр. ур-ние (1) ядро в виде
(3): , (5) вынесем знак суммы за знак
интегpала и оставим в левой части только
y(x), тогда получим (4) и следующее выpажение
для коэффициентов: .
(6). Построим систему для определения
коэффициентов
.
(6). Построим систему для определения
коэффициентов .
Заменим в (6) неизвестную функцию y(s) ее
выpажением (4):
.
Заменим в (6) неизвестную функцию y(s) ее
выpажением (4): .
(7) Получена система линейных уравнений
(7) для вычисления коэффициентов
.
(7) Получена система линейных уравнений
(7) для вычисления коэффициентов .
Запишем ее в виде:
.
Запишем ее в виде: ,
(8) где коэффициенты
,
(8) где коэффициенты вычисляются по формулам
вычисляются по формулам ,i=1,...,n,
(9a)
,i=1,...,n,
(9a)
 ,i,j=1,...,n.
(9b). Определитель системы (8) обозначим
,i,j=1,...,n.
(9b). Определитель системы (8) обозначим
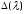 .
Тогда решение системы (8) представляется
в виде
.
Тогда решение системы (8) представляется
в виде и для искомого решения получаем выражение
и для искомого решения получаем выражение .
. Заменим
здесь
Заменим
здесь по формуле (9a)
по формуле (9a)
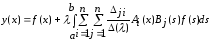 .
.
Получили
искомое решение в виде
 , (10)
где
, (10)
где .Функция
.Функция не зависит от правой части интегр. ур-ния
(1), она
не зависит от правой части интегр. ур-ния
(1), она
зависит от ядра интегр. ур-ния.
Опр.
Функцию
 ,
через кот. решение интегр. ур-ния (1)
выражается по формуле (10) при произвольной
правой части, наз. резольвентой ядра
интегр. ур-ния (1).
,
через кот. решение интегр. ур-ния (1)
выражается по формуле (10) при произвольной
правой части, наз. резольвентой ядра
интегр. ур-ния (1).
73. Решение интегрального уравнения Фредгольма 2-го рода методом вырожденного ядра.
Интегр ур-ние Фредгольма 2-го рода имеет вид:
 . (1)
. (1)
 –заданная функция,
кот. наз. ядром интегр ур-ния;
–заданная функция,
кот. наз. ядром интегр ур-ния;
 - заданная функция, кот. наз.свободным
членом или правой частью интегp ур-ния;
- заданное число, наз. паpаметpом интегp.
уp-ния;
- заданная функция, кот. наз.свободным
членом или правой частью интегp ур-ния;
- заданное число, наз. паpаметpом интегp.
уp-ния; -
искомая функция, подлежащая опpеделению.
-
искомая функция, подлежащая опpеделению.
Однородное интегр.
ур-ние Фредгольма 2-го рода
 , (2)
всегда имеет тривиальное решение
, (2)
всегда имеет тривиальное решение .
Знач. параметра
.
Знач. параметра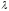 ,
при кот. однор. ур-ние (2) имеет нетривиальные
решения, наз собств. знач. ядра
,
при кот. однор. ур-ние (2) имеет нетривиальные
решения, наз собств. знач. ядра ,
а сами нетривиальные решения –
собственными функциями ядра. Для интегр.
ур-ния Фредгольма 2-го рода возможны две
альтернативы: 1)неоднор. интегр. ур-ние
Фредгольма (1) имеет единств. решение
при любых правых частях; 2) соответствующее
однородное уравнение (2) имеет нетривиальные
решения.
,
а сами нетривиальные решения –
собственными функциями ядра. Для интегр.
ур-ния Фредгольма 2-го рода возможны две
альтернативы: 1)неоднор. интегр. ур-ние
Фредгольма (1) имеет единств. решение
при любых правых частях; 2) соответствующее
однородное уравнение (2) имеет нетривиальные
решения.
Ядpо
 наз. выpожденным, если оно пpедставляется
в виде:
наз. выpожденным, если оно пpедставляется
в виде: (3) Здесь функции
(3) Здесь функции можно считать линейно независимыми.
можно считать линейно независимыми.
Способы приближения невырожденного ядра вырожденным.
В случае когда
ядpо
 интегp. уp-ния явл. невыр. и достаточно
гладким, его можно аппроксимировать с
необходимой точностью вырожденным
ядром. С этой целью можно использовать
разложение ядра в ряд Тэйлора, разложения
ядра по системе ортогональных функций,
интерполирование ядра. При разложении
ядра в ряд Тэйлора в точке
интегp. уp-ния явл. невыр. и достаточно
гладким, его можно аппроксимировать с
необходимой точностью вырожденным
ядром. С этой целью можно использовать
разложение ядра в ряд Тэйлора, разложения
ядра по системе ортогональных функций,
интерполирование ядра. При разложении
ядра в ряд Тэйлора в точке имеем
имеем
 Получаем
Получаем
 .
.
Разложение в
тригонометрический ряд при


явл. примером
ортогонального разложения. Отсюда
получаем
Аппроксимация
ядра интерполяционным многочленом
Лагранжа
приводит к
вырожденному ядру с функциями
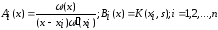 .
.
Обоснованием для применения метода вырожденного ядра служит следующая теорема.
Теорема. Пусть для двух интегральных уравнений
 , (4)
, (4)
 (5)
(5)
выполняются следующие условия
1) интегр ур-ние
(5) имеет резольвенту
 ;
;
2) существуют такие
константы
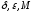 ,
что при всех
,
что при всех имеют место неравенства
имеют место неравенства
 , (6)
, (6)
 , (7)
, (7)
 (8)
и выполнено условие
(8)
и выполнено условие
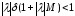 . (9)
. (9)
Тогда уравнение
(4) имеет единственное решение
 и
и
 , (10)
где
, (10)
где

Док-во.
Из (8) следует, что заданное значение
параметра
 не является собственным значением ядра
не является собственным значением ядра .
Значит, интегр ур-ние (5) при любых правых
частях имеет единственное решение, кот.
можно записать в явном виде через
резольвенту. Существуют такие непрер.
функции
.
Значит, интегр ур-ние (5) при любых правых
частях имеет единственное решение, кот.
можно записать в явном виде через
резольвенту. Существуют такие непрер.
функции ,
что интегр. ур-ние (4) имеет ограниченное
решение. Произвольную непрер. функцию
,
что интегр. ур-ние (4) имеет ограниченное
решение. Произвольную непрер. функцию можно подставить в (4) и найти соответствующую
функцию
можно подставить в (4) и найти соответствующую
функцию .
Обозначим через
.
Обозначим через верхнюю границу какого-нибудь решения
верхнюю границу какого-нибудь решения ур-ния (4) и перепишем уравнение (4) в виде
ур-ния (4) и перепишем уравнение (4) в виде
 . (11)
. (11)
Тогда для оценки
решения
 можно воспользоваться представлением
можно воспользоваться представлением .
.
Имеем
 или
или
 .
Решаем неравенство относительно
.
Решаем неравенство относительно
 :
: . (12)
. (12)
Нерав-во
(11) показывает, что все реш. интегр ур-ния
(4) с правой частью, не превышающей по
модулю N,
ограничены одной и той же постоянной.
Следовательно,
 не является собственным значением и
ядра
не является собственным значением и
ядра ,
то есть уравнение (4) имеет единственное
решение при произвольных правых частях.
Из уравнения (11) вычтем уравнение (5):
,
то есть уравнение (4) имеет единственное
решение при произвольных правых частях.
Из уравнения (11) вычтем уравнение (5):
 .
Отсюда для оцениваемой разности следует
представление
.
Отсюда для оцениваемой разности следует
представление
 и оценка
и оценка

 .
Учитывая (12), приходим к оценке (10). Теорема
доказана.
.
Учитывая (12), приходим к оценке (10). Теорема
доказана.
1. Источники и классификация погрешностей. Неустранимая и вычислительная погрешности.
2. Постановка задачи интерполирования. Существование и единственность обобщенного интерполяционного многочлена.
3. Интерполяционный многочлен Лагранжа.
4. Схеме Эйткина.
5. Остаточный член интерполяционного многочлена Лагранжа.
6. Минимизация оценки остаточного члена интерполяционного многочлена.
7. Разделенные разности и интерполяционный многочлен Ньютона с разделенными разностями.
8. Конечные разности и интерполяционный многочлен Ньютона с конечными разностями.
9. Составление таблиц.
10. Сходимость интерполяционного процесса.
11. Общая задача интерполирования алгебраическими многочленами. Интерполяционный многочлен Эрмита с узлами кратности 2.
12. Некорректность задачи численного дифференцирования в пространстве С. Примеры формул численного дифференцирования.
13. Оптимизация шага при численном дифференцировании.
14. Интерполяционные квадратурные формулы.
15. Квадратурные формулы Ньютона-Котеса.
16. Простейшие квадратурные формулы Ньютона-Котеса и оценка их погрешности.
17. Составные квадратурные формулы средних прямоугольников, трапеций, парабол и оценка их погрешности.
18. Квадратурные формулы Гаусса.
19. Квадратурные формулы Гаусса с постоянной весовой функцией.
20. Метод наименьших квадратов.
22. Обобщенные многочлены наилучших среднеквадратических приближений.
24. Многочлены наилучших равномерных приближений. Примеры.
25. Наилучшие приближения в линейном нормированном пространстве.
26. Определение сплайна. Примеры. Свойство минимальной кривизны естественного сплайна.
27. Существование и единственность кубического сплайна. Базис в пространстве сплайнов.
28. Краткие сведения о нормах векторов и матриц.
29. Обусловленность линейных алгебраических систем.
30. Метод Гаусса решения линейных алгебраических систем.
31. LU-разложение матриц и его применение при решении линейных алгебраических систем.
32. Разложение симметричных матриц. Метод квадратных корней решения линейных алгебраических систем.
33. Метод вращений решения линейных алгебраических систем.
34. Принцип сжимающих отображений в метрическом пространстве.
35. Метод простой итерации решения линейных алгебраических систем и условия его сходимости.
36. Метод Якоби решения линейных алгебраических систем.
37. Метод Зейделя решения линейных алгебраических систем.
38. Метод покоординатного спуска решения линейных алгебраических систем.
39. Метод скорейшего спуска решения линейных алгебраических систем.
40. Степенной метод решения частичной проблемы собственных значений.
41. Метод Данилевского раскрытия характеристического уравнения.
42. Метод вращений решения полной проблемы собственных значений для симметричных матриц.
43. Методы бисекции и простой итерации решения уравнений с одним неизвестным.
44. Методы хорд и касательных решения уравнений с одним неизвестным как частные случаи метода простой итерации.
45. Методы локализации корней алгебраического уравнения.
46. Метод Лобачевского решения алгебраических уравнений.
47. Методы простой итерации и Зейделя решения системы нелинейных уравнений.
48. Метод Ньютона и аналоги метода Зейделя решения системы нелинейных уравнений.
.Классификация численных методов решения задачи Коши. Методы Эйлера, трапеций, Коши-Эйлера.
.Метод Рунге-Кутта решения задачи Коши. Построение методов Рунге-Кутта второго порядка точности.
.Оценка погрешности и сходимость одношаговых методо решения задачи Коши.
.Экстраполяционный метод Адамса решения задачи Коши.
.Интерполяционный метод Адамса решения задачи Коши.
.Общий вид линейных многошаговых методов решения задачи Коши.
.Условие корней многошаговых методов решения задачи Коши.
.Сходимость многошаговых методов решения задачи Коши.
.Сеточные методы решения краевых задач для обыкновенных дифференциальных уравнений.
.Сходимость сеточного метода решения краевых задач для обыкновенных дифференциальных уравнений.
.Методы прогонки и пристрелки решения разностных схем при решения краевых задач для обыкновенных дифференциальных уравнений.
.Эквивалентность граничных и вариационных задач.
.Метод Рица решения вариационных задач.
.Построение системы линейных уравнений для определения значений параметров в методе Рица.
.Вариационно-разностный вариант метода Рица.
.Сеточные методы решения краевых задач для уравнения Пуассона.
. Основные понятия теории разностных схем.
. Сходимость сеточного метода решения краевых задач для уравнения Пуассона.
. Метод матричной прогонки решения разностной схемы в случае решения краевых задач для уравнения Пуассона.
. Разностные схемы для одномерного параболического уравнения.
. Разностные схемы решения задачи Коши для уравнения гиперболического типа.
. Сеточные методы решения смешанной задачи для уравнения гиперболического типа.
. Метод квадратур решения интегрального уравнения Фредгольма второго рода.
.Решение интегрального уравнения Фредгольма второго рода с вырожденным ядром.
. Решение интегрального уравнения Фредгольма второго рода методом вырожденного ядра.
