
- •1.Источники и классификация погрешностей. Неустранимая и вычислительная погрешность.
- •2. Постановка задачи интерполирования. Существование и единственность обобщенного интерполяционного многочлена.
- •3. Интерполяционный многочлен Лагранжа.
- •4. Схема Эйткина
- •5. Остаточный член интерполяционного многочлена Лагранжа.
- •6. Минимиз. Оценки остаточного члена интерпол. Мн-на.
- •7. Разделенные разности и интерполяционная формула Ньютона с разделенными разностями.
- •8. Конечные разности и интерполяционные формулы Ньютона с конечными разностями.
- •9. Составление таблиц.
- •10. Сходимость интерполяционного процесса
- •11.Общая задача интерполирования алгебраическими многочленами. Интерполяционный многочлен Эрмита с узлами кратности 2.
- •13 . Оптимизация шага при численном диф-нии
- •14. Интерполяционные квадратурные формулы
- •15. Квадратурные формулы Ньютона-Котеса
- •16. Простейшие квадрат ф-лы н-Кот. И оценка их погрешности.
- •17. Составные квадратурные формулы средних прямоугольников, трапеций, парабол и оценка их погрешности
- •18. Квадратурные формулы Гаусса
- •20. Метод наименьших квадратов.
- •22.Обобщённые мног-ны наилучших среднеквадратических приближений.
- •24. Многочлены наилучших равномерных приближений. Примеры.
- •25. Наилучшие приближения в линейном нормированном пространстве.
- •26. Интерполяционные сплайны.
- •27. Существование и единственность кубического сплайна.
- •28.Краткие сведения о нормах векторов и матриц.
- •29. Обусловленность линейных алгебраических систем.
- •30. Метод Гаусса решения системы линейных ур-ний.
- •31. - Разложение квадратных матриц.
- •32. Разложение симметричных матриц. Метод квадр. Корней решения лин. Алг.Систем
- •34. Принцип сжимающих отображений в метрическом пространстве.
- •35. Метод простой итерации решения лин. Алг. Систем и усл. Его сходимости.
- •36. Метод Якоби решения линейных алгебраических систем
- •37. Метод Зейделя решения лин. Алг. Систем.
- •38. Метод покоординатного спуска решения линейных алгебраических систем.
- •39. Метод скорейшего спуска решения линейных алгебраических систем
- •40. Степенной метод решения частичной проблемы собственных значений.
- •41. Метод Данилевского раскрытия характеристического уравнения
- •42. Метод вращений решения полной проблемы собственных значений.
- •43. Метод бисекции и простой итерации решения уравнений с одним неизвестным.
- •44. Методы хорд и касательных как частные случаи метода простой итерации.
- •45. Методы локализации корней алгебраического уравнения.
- •46. Метод Лобачевского решения алгебраических уравнений.
- •47. Методы простой итерации и Зейделя решения системы нелинейных уравнений.
- •48. Метод Ньютона и аналоги метода Зейделя решения системы нелинейных уравнений.
- •49. Классификация численных методов решения задачи Коши. Методы Эйлера, трапеций и к-э.
- •50. Метод Рунге-Кутта решения задачи Коши. Построение методов р-к второго порядка точности.
- •51. Оценка погрешности и сходимость одношаговых методов решения задачи Коши.
- •52. Экстраполяц. Метод Адамса решения задачи Коши.
- •53. Интерполяционный метод Адамса решения задачи Коши.
- •54. Общий вид линейных многошаговых методов решения задачи Коши.
- •55. Условие корней многошаговых методов решения задачи Коши
- •56. Сходимость многошаговых методов решения Коши.
- •57. Сеточные методы решения краевых задач для обыкновенных дифференциальных уравнений.
- •58. Сходимость сеточного метода решения краевых задач для обыкновенных диф. Уравнений.
- •59. Методы прогонки и пристрелки решения разностных схем при решении краевых задач для обыкновенных д.У.
- •60. Эквивалентность граничных и вариационных задач
- •61. Метод Ритца решения вариационных задач.
- •62. Построение системы линейных уравнений для определения значений параметров в методе Ритца.
- •63. Вариационно-разностный вариант метода Рица.
- •64. Сеточные методы решения краевой задачи для уравнения Пуассона. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •Постpоение pазностной схемы
- •65. Основные понятия теории разностных схем.
- •66. Сходимость сеточного метода
- •Фоpмулиpовка исходной дифференциальной краевой задачи
- •67.Метод матричной прогонки решения разностной схемы. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •68. Разностные схемы для одномерного параболического уравнения. Фоpмулиpовка исходной диффеpенциальной задачи
- •69. Разностные схемы решения задачи Коши для уравнения гиперболического типа.
- •70. Сеточные методы решения смешанной задачи для уравнений гиперболического типа.
- •71. Метод квадратур решения интегрального уравнения Фредгольма 2-го рода.
- •72. Решение интегрального уравнения Фредгольма 2-го рода с вырожденным ядром.
- •Решение интегр. Ур-ния с вырожденным ядром.
- •73. Решение интегрального уравнения Фредгольма 2-го рода методом вырожденного ядра.
- •Способы приближения невырожденного ядра вырожденным.
50. Метод Рунге-Кутта решения задачи Коши. Построение методов р-к второго порядка точности.
Рассмотрим
задачу Коши
 (1)
(1) ,y(a)=y0
(2).
Будем предполагать, что задача (1)(2) на
,y(a)=y0
(2).
Будем предполагать, что задача (1)(2) на
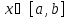 имеет точное решениеy(x).
Определим сетку a=x0<x1<……..<xn=b.
Методы Рунге-Кутта опред. 3 наборами
параметров
имеет точное решениеy(x).
Определим сетку a=x0<x1<……..<xn=b.
Методы Рунге-Кутта опред. 3 наборами
параметров

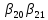
…………….. ( )
)


(3). Алгоритм задается так:
1)полагаем

2)
вычисляем функции

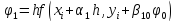
…

3)
вычисляем

4)
вычисляем
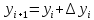
Рассмотрим
схему построения методов Рунге – Кутта
в случае q=1.
В этом случае метод явл. 2 порядка
точности, при q=1
исп. 4 параметра:
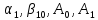 .
.
Расчетная
ф-ла примет вид
 (3).
(3).
Обозначим
через
 интегральную кривую уравнения (1), проход
через точку
интегральную кривую уравнения (1), проход
через точку ,
удовлетворяющую условию
,
удовлетворяющую условию .
Подставляя ее в (3) получим
.
Подставляя ее в (3) получим (4)
(4)
разложим левую и правую части равенства (4) по степеням h. Для левой части будем иметь
 ,
где
,
где
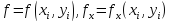 ,
где
,
где ,
,
Правую
часть рассмотрим как сложную ф-цию
переменной h
и произведем разложение в нуле. Будем
иметь
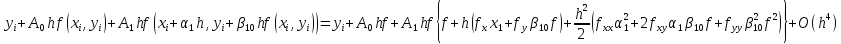
Разложение в левых и правых частях слагаемые совпадают
 .
.
Т.о. для определения 4 параметров метода получаем

Задавая
произвол образом
 легко найдем остальные парам-ы
легко найдем остальные парам-ы т.о. приq=1
получим бесконеч. методов Рунге-Кутта
2-го порядка точн-и. Иногда исп. термин
однопараметр-ое семейство Рунге-Кутта.
При
т.о. приq=1
получим бесконеч. методов Рунге-Кутта
2-го порядка точн-и. Иногда исп. термин
однопараметр-ое семейство Рунге-Кутта.
При
 ,
, ,
,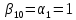 получаем метод Коши Эйлера.
получаем метод Коши Эйлера.
51. Оценка погрешности и сходимость одношаговых методов решения задачи Коши.
Рассмотрим
 (1)
(1) (2).
Пусть задача Коши (1), (2) имеет точное
решение
(2).
Пусть задача Коши (1), (2) имеет точное
решение .
На отрезке
.
На отрезке зададим сетку
зададим сетку .
Для численного решения задачи Коши (1),
(2) будем использ. одношаг. метод с
расчетной формулой вида
.
Для численного решения задачи Коши (1),
(2) будем использ. одношаг. метод с
расчетной формулой вида (3). Приближ. значения решения задачи
Коши в узлах сетки
(3). Приближ. значения решения задачи
Коши в узлах сетки ,
получаемые реально при вычисл. по формуле
(3), обозн. через
,
получаемые реально при вычисл. по формуле
(3), обозн. через .
Эти значения удовл. Рав-ам
.
Эти значения удовл. Рав-ам (4).
Здесь
(4).
Здесь - вычислит. погр-ть на шаге при вычислениях
по формуле (3). Обозначим через
- вычислит. погр-ть на шаге при вычислениях
по формуле (3). Обозначим через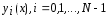 точные решения задач Коши
точные решения задач Коши (5),
(5), (6).
Подставляя в (3)
(6).
Подставляя в (3) имеем
имеем
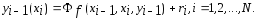 (7).
Здесь
(7).
Здесь
 - погр-ть метода на соотв. шаге. Вычитая
из равенств (7) равенства (4), получим
общую погр-ть на шаге
- погр-ть метода на соотв. шаге. Вычитая
из равенств (7) равенства (4), получим
общую погр-ть на шаге . (8).
Проведем оценку погрешности
. (8).
Проведем оценку погрешности решения задачи Коши, получаемого по
расчетной формуле (3) в узле
решения задачи Коши, получаемого по
расчетной формуле (3) в узле .
Очевидно, искомую погрешность можно
записать в виде
.
Очевидно, искомую погрешность можно
записать в виде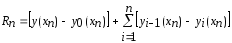 . (9).
Здесь
. (9).
Здесь - неустранимая погр-ть решения в узле
- неустранимая погр-ть решения в узле ,
которая вызвана погр-ю
,
которая вызвана погр-ю задания нач. условия; а по-ть
задания нач. условия; а по-ть вызвана пог-ми метода и вычислит.
вызвана пог-ми метода и вычислит. на соотв. шаге. Для проведения преобразований
в формуле (9) нам понадобится след. лемма.Лемма.
Пусть
на соотв. шаге. Для проведения преобразований
в формуле (9) нам понадобится след. лемма.Лемма.
Пусть
 - решения д. у.
- решения д. у. где
где - непрерывная и непрерывно диф-я по
переем.
- непрерывная и непрерывно диф-я по
переем. ф-я. Тогда
ф-я. Тогда (10),
где
(10),
где заключено между
заключено между и
и .Док-во.
По условию леммы
.Док-во.
По условию леммы
 ,
, .
. .
Здесь
.
Здесь заключено между
заключено между и
и .
Так как
.
Так как явл. на расс-ом отрезке непрерывной
ф-ей, то
явл. на расс-ом отрезке непрерывной
ф-ей, то ,
а отсюда следует (10). Лемма доказана.
Использ. доказ. лемму, преобр. выражение
(9) к виду
,
а отсюда следует (10). Лемма доказана.
Использ. доказ. лемму, преобр. выражение
(9) к виду
 . (11)
. (11)
Здесь
 заключено между
заключено между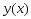 и
и ,
а
,
а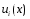 - между
- между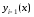 и
и .
. Пусть
имеют место оценки
Пусть
имеют место оценки
 и
и
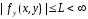 в рассматр. области изменения аргументов.
Тогда из (11) имеем следующую оценку
искомой погр-ти
в рассматр. области изменения аргументов.
Тогда из (11) имеем следующую оценку
искомой погр-ти .
Обознач.
.
Обознач. .
Т.к.
.
Т.к. ,
то оценку можно переписать в виде
,
то оценку можно переписать в виде
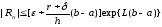 . (12).
Введем обозначение
. (12).
Введем обозначение
 .
На основании оценки (12) сформулируем
достаточные условия сходимости.
Одношаговый метод с расчетной формулой
(3) сходится, если
.
На основании оценки (12) сформулируем
достаточные условия сходимости.
Одношаговый метод с расчетной формулой
(3) сходится, если ,
, при
при . (13).
Итак, получена искомая оценка погрешности
(12) и достаточные условия сходимости
(13).
. (13).
Итак, получена искомая оценка погрешности
(12) и достаточные условия сходимости
(13).
