36. Метод Якоби решения линейных алгебраических систем

Рассмотрим систему линейных алгебраических уравнений (1)

Представим матрицу в виде:, где

, ,. Тогда (1) перепишем в виде:

(2)

Предположим, что , . Тогда существует и (2) можно записать в виде:

(3)

К (3) применим метод простой итерации:

(4)

Метод, определяемый формулой (4), называется методом Якоби.

Теорема Если матрица имеет диагональное преобразование, то метод, определяемый расчетной формулой (4), сходится.

Док-во Обозначим . Тогда

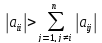Диагональное преобразование матрицы обозначает, что следует .

Отсюда . Теорема доказана.

Отметим, что для сходимости метода (4) необходимо и достаточно, чтобы все корни уравнения:

были по модулю . Последнее уравнение равносильно уравнению: . Откуда следует теорема.

Теорема Для сходимости метода (4) необходимо и достаточно, чтобы все корни уравнения:

по модулю были .

Замечание К системе уравнений, записанных в форме (3), можно применить метод Зейделя.

Такой метод всегда будет сходится, если матрица имеет диагональные преобразование или матрицаявляется положительно определенной системой. Отметим, что любую систему (1) всегда можно записать системой: симметричной положительной определенной матрицей.

37. Метод Зейделя решения лин. Алг. Систем.

Метод Зейделя применяется для решения систем линейных алгебраических уравнений, заданных в виде . (1)

Здесь исходными данными являются - квадратная матрица порядкаn и вектор . Метод Зейделя решения системы алгебраических уравнений (1) описывается расчетной формулой

. (2)

Введем в рассмотрение матрицы

и , гдеF=B*H.

С их использованием расчетную формулу (2) можно записать в матрично-векторной форме

. (2’)

Отсюда имеем . (3)

Теорема 1. Для сходимости метода Зейделя (2) при любом начальном приближении необходимо и достаточно, чтобы все собственные значения матрицы по модулю были меньше единицы.

Теорема 2. Если выполняется одно из условий

1) ; 2),

то метод Зейделя (2) сходится.

Доказательство. По теореме 1 все собственные значения матрицы по модулю должны быть меньше единицы. Собственные значения являются решениями уравнения. Так как, то отсюда следует равносильное уравнение

Проведем доказательство теоремы для случая, когда выполняется условие 1). Допустим, что существует собственное значение , такое, чтои. Тогда система однородных уравнений

(4) должна иметь нетривиальное решение, для которого . Из уравненияi системы (4) получаем

. (5)

Для суммы модулей недиагональных элементов в уравнении i системы (4) имеем оценку

, что противоречит равенству (5).

38. Метод покоординатного спуска решения линейных алгебраических систем.

Этот метод предназначен для решения системы линейных алгебраических уравнений (1) с вещественной симметричной положительно определенной матрицей. Обозначим решение системы (1) через. Из положительной определенности и симметричности матрицы следует

,

При этом знак равенства возможен лишь при . Отсюда видно, что минимум функционала

(2) достигается на решении 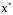системы (1). Т. о., решение системы (1) сводится к минимизации функционала. Для минимизации функционала воспользуемся методом покоординатного спуска. Обозначим начальное приближение через. Пусть уже найдено приближениеи компоненты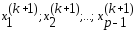приближения. Рассмотрим, как в методе покоординатного спуска вычисляется значение очередной компоненты. Найдем частную производную функционала по координате:

Значение этой производной в точке определяет скорость изменения функционала при движении из этой точки в направлении координатной оси. Очевидно, минимальное значение функционал будет достигать на рассматриваемом координатном направлении в точке, где частная производная равна нулю. Таким образом, для нахожденияполучаем уравнение с одним неизвестным:

.

Отсюда получаем расчетные формулы метода покоорд. спуска: (3)

Вычисления прекращаются при достижении заданной точности , то есть при значенииk, для которого выполняются условия . (4)

Метод покоординатного спуска с расчетными формулами (3) называют обычно методом Зейделя.

Теорема. Если матрица A сим-ая и положит. определен., то последовательные приближения , построенные по методу покоорд. спуска, сходятся к решению системысо скоростью геометрической прогрессии.

Доказательство. Метод Зейделя (3) эквивалентен методу простой итерации , (5) где элементы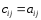прии равны нулю в остальных случаях,. Вычитая из (5) равенство, получаем равенство(6) для погрешностей.

Пусть . Тогда хотя бы одно уравнение системы (1) не удовлетворяется и по формулам (3) будет найдено приближение, для которого вып-ся нер-во, то есть,

. (7)

Отметим, что (7) выполняется для любого . Рассмотрим функцию. Эта функция непрерывна на единичной сфереи поэтому принимает на ней свое максимальное значение. Т. о.,и.

У симметричной положительно определенной матрицы все собственные значения положительны и существует полная ортонормированная система собственных векторов. Раскладывая векторs по собственным векторам матрицы A, имеем ,,, откуда

. (8)

Следовательно, для погрешности можно записать оценку

,

которая показывает, что норма погрешности стремится к нулю, как геометрическая последовательность со знаменателем 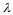. Теорема доказана.