2. Постановка задачи интерполирования. Существование и единственность обобщенного интерполяционного многочлена.

Интерполирование или интерполяция – это один из наиболее часто применяемых на практике методов приближения функций. Задача интерполирования ставится следующим образом.

Рассмотрим пространство функций, определенных на отрезке. Пусть в пространстве задана последовательность линейно независимых функций . Пусть также на отрезкезадана последовательность попарно неравных точекпри. Образуем линейную комбинацию(1)

Линейную комбинацию вида (1) называют обобщенным многочленом по системе функций .

Систему функций называют системой Чебышева на отрезке, если любой нетривиальный обобщенный многочлен по этой системе обращается в нуль на отрезкене более чем вn точках.

В задаче интерполирования функцию нужно приблизить обобщенным многочленом (1) так, чтобы значения функции и обобщенного многочлена совпадали в заданных точках:

. (2)

Обобщенный многочлен , удовлетворяющий условиям (2), называют интерполяционным обобщенным многочленом. При этом функцию, для которой строится интерполяционный обобщенный многочлен, называют интерполируемой функцией, а точкиназывают узлами интерполяции. Равенства (2) будем называть интерполяционными условиями.

Теорема существования и единственности интерполяционного обобщенного многочлена. Для того чтобы для любой функции при любых наборах попарно неравных узлов существовал интерполяционный обобщенный многочлен по системе функций, необходимо и достаточно, чтобы эта система функций была системой Чебышева на отрезке. При этом интерполяционный обобщенный многочлен будет единственным.

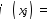
Доказательство. Возьмём из (1) интерполяционные условия (1)

Интерполяционные условия представляют собой систему линейных алгебраических уравнений относительно неизвестных коэффициентов . Система (1) имеет решение при любых правых частях тогда и только тогда, когда ее определительотличен от нуля.

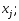
Докажем необходимость. Допустим противное: при любых наборах попарно неравных узлов на отрезке , а система функций не является системой Чебышева на этом отрезке. Тогда существует нетривиальный обобщенный многочлен, который обращается в нуль наболее чем вn точках. Возьмем n+1 из них в качестве узлов . Следовательно,. Это означает, что столбцы определителялинейно зависимы и. Полученное противоречие доказывает необходимость.

Достаточность. Допустим противное: система функций является системой Чебышева на отрезке, апри некотором наборе попарно неравных узлов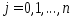на этом отрезке. Следовательно, столбцы определителя линейно зависимы:. Последнее означает, что нетривиальный обобщенный многочленобращается в нуль наболее, чем вn точках, то есть, система функций не является на этом отрезке системой Чебышева. Полученное противоречие доказывает достаточность.

Поскольку при система (1) имеет единственное решение, то интерполяционный обобщенный многочлен также будет при этом единственным. Теорема доказана.

3. Интерполяционный многочлен Лагранжа.

Запишем решение с-мы (1) по ф-лам Крамера и выполним разложениепо столбцуi: . Т.о., инт. об. мн-н м. представить в виде (2)

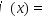
.Интерполяционный многочлен Лагранжа. С-ма ф-ций , (1) в силу осн. теоремы алгебры, явл. с-мой Чебышева на любом отрезке. Для любой ф-циипо этой с-ме ф-ий при любом наборе попарно неравных узлов! инт. обоб. мн-н, к-ый м. б. записан в виде, (2) где обоб. мн-ныне зависят от ф-ии.Зафикс.j и рассм. ф-ию , приним. в узлах значения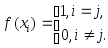 Для этой ф-ии имеем инт. обоб. мн-н . Т.к. вып-ся инт. усл-я, то. Т.о., для обоб. мн-новимеет место св-во(3) Если построить обоб. мн-ны, удовл. св-ву (3), то тем самым б. построен инт. обоб. мн-н (2). Для с-мы ф-ий(1),очевидно, мн-ныобл. св-м (3). Т.о., по с-ме ф-ий (3) инт-ый мн-н получается в виде(4). (4) наз. инт.мн-м Лагранжа для ф-ипо. Обозн..имееми.С исп-ем мн-наинт.мн-н Лагранжа примет вид. (4’)