34. Принцип сжимающих отображений в метрическом пространстве.

Теорема (принцип сжимающих отображений). Пусть в полном метрическом пространстве задан операторA, осуществляющий сжатое отображение этого пространства в себя. Тогда оператор A в пространстве имеет единственную неподвижную точку, то есть, уравнениеимеет в пространствеединственное решение. Эта неподвижная точка может быть найдена как предел последовательности, образованной по правилу

(1) при .

Доказательство. Возьмем произвольное , зафиксируем его и построим последовательность (1). Докажем, что построенная последовательность является фундаментальной. Для этого оценим расстояниев предположении.

Так как оператор A сжимающий, то существует положительное число , такое, что. Повторяя эти рассуждения, получаем оценку. (2)

По аксиоме треугольника имеем . Применяя оценку (2) к каждому слагаемому в правой части последнего неравенства, получим

. (3)

Из оценок (2) и (3) следует оценка

, (4) доказывающая фундаментальность последовательности (1).

Фундаментальная последовательность в полном пространстве имеет предел . Покажем, что этот предел является неподвижной точкой оператораA. Перейдем к пределу в равенстве (1). Так как предел левой части существует , то существует и предел правой части. Покажем, что предел правой части равен. Действительно,. Таким образом,.

Осталось доказать единственность неподвижной точки. Допустим противное: пусть существуют две неподвижные точки . Тогда имеем. Полученное противоречие доказывает единственность. Теорема доказана.

35. Метод простой итерации решения лин. Алг. Систем и усл. Его сходимости.

Пусть система линейных алгебраических уравнений получена в виде. (1) Здесь заданыквадратная матрица порядка n и вектор.

Метод простой итерации решения системы алгебраических уравнений (1) описывается расчетной формулой.,(2) что соответствует скалярной записи.(2’)

Для проведения вычислений по расчетной формуле (2) требуется задать начальное приближение к решению.Достаточные условия сходимости метода простой итерации определяет следующая

Теорема 1. Если какая-либо подчиненная норма матрицы меньше единицы, то метод простой итерации (2) сходится при любом начальном приближении.До-во. Пространство n-мерных векторов, очевидно, является полным. Определим в нем оператор A равенством. Очевидно, этот оператор отображает векторное пространство в себя. Возьмем произвольные векторы. Для них выполняется равенство

.(3)

В выражении (3) используется векторная норма. Для нормы матрицы, подчиненной этой векторной норме, будет выполняться неравенство

.(4)

Отсюда следует, что при отображениебудет сжимающим и будут выполнены все условия принципа сжатых отображений из параграфа 3. Таким образом, последовательность, образованная по правилубудет сходиться при любом начальном приближении. Теорема доказана.

Теорема 2. Если выполняется одно из следующих трех условий

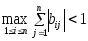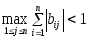1) , 2), 3),

где - собственные значения матрицы,

то метод простой итерации (2) сходится.

Доказательство. Матричная норма, подчиненная векторной, по определению равна . Для кубической нормы вектора, определяемой равенством, получаем

Отсюда определяется кубическая норма матрицы . Аналогично определяется октаэдрическая норма матрицы, подчиненная октаэдрической векторной норме.Евклидова векторная норма, называемая еще сферической, определяется равенствоми сферическая норма векторавыражается формулой. Так как вещественная симметричная матрицаобладает полной ортонормированной системой собственных векторови положительными собственными значениями, то можно воспользоваться разложениеми получитьи.

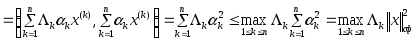Отсюда следует, что .

Таким образом, теорема 2 является следствием теоремы 1 для кубической, октаэдрической и сферической норм матрицы, подчиненных соответствующим векторным нормам. Теорема 2 доказана.

Теорема 3. Для того чтобы метод простой итерации (2) сходился при любом начальном приближении необходимо и достаточно, чтобы все собственные значения матрицы B по модулю были меньше единицы.

До-во. Необx. Из равенств (2) вычтем равенство , тогда для погрешностиполучим равенства(5)

Возьмем начальное приближение так, чтобы его погрешностьбыла собственным вектором матрицы B, соответствующим собственному значению, для которого. В этом случае имеем, то есть, погрешность не стремится к нулю. Необходимость доказана.Достаточность. Возьмем произвольное положительное число и рассмотрим матрицу. Для собственных значений матриц, очевидно, выполняются равенства. Как известно из линейной алгебры, для любой квадратной матрицы S существует неособенная матрица Q, такая, что преобразование подобия с ней приводит матрицу S к модифицированной жордановой форме:. На главной диагонали матрицынаходятся собственные значения, на наддиагонали – единицы и нули, остальные элементы равны нулю. Преобразование подобия не меняет собственных значений. Определим векторную норму равенством.Поскольку, то для подчиненной ей нормы матрицы B имеем

.

Таким образом при достаточно большом выполняется неравенствои по теореме 1 метод простой итерации (2) сходится при любом начальном приближении. Теорема доказана.