10. Сходимость интерполяционного процесса

Рассмотрим последовательность интерполяционных многочленов , которые строятся для функциипо системе узлов. Говорят, что задаваемая при этом треугольная матрица

(1) определяет интерпол-ный процесс.

Интерполяционный процесс называется сходящимся, если . (2)

Если сходимость выражения (2) равномерная, т.е. прито интерполяционный процесс называют равномерно сходящимся.

Теорема.Для целой функции интерполяционный процесс сходится на отрезкеравномерно.

Д-во. Целая функция по определению представляется в виде степенного ряда

, (3)

сходящегося при всех значениях x. Пусть остаточный член интерпол. Многочлена Лагранжа.Так как целая функция имеет производные любого порядка, то можно воспользоваться оценкой

, (4)

где . Покажем, что правая часть в неравенстве (4) стремится к нулю при.

Дифференцируя (3), имеем

(*)

(*) перепишем ввиде

Отсюда получим

Из неравенства приследует. Т.о.,.

Умножим обе части последнего неравенства на , гдеS – произвольное, но фиксированное положительное число:

.

Вводя обозначение , отсюда имеем.

Так как последнее неравенство справедливо для всех , то получаем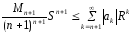. (5)

Из теоремы Абеля следует, что степенной ряд (3), сходящийся на всей числовой оси, сходится абсолютно и равномерно на любом отрезке, то есть, при любом фиксированном правая часть в неравенстве (5), а значит и левая при любом фиксированном, стремится к нулю при. Представим правую часть неравенства (4) в виде

.

С учетом очевидного неравенства имеем

.

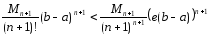Принимая , получаеми приходим к искомому результатус равномерной сходимостью на. Теорема доказана.

11.Общая задача интерполирования алгебраическими многочленами. Интерполяционный многочлен Эрмита с узлами кратности 2.

Общая задача интерполирования обобщенными многочленами формулируется следующим образом. Для функции и набора попарно неравных узловтребуется построить обобщенный многочленпо системе функцийтак, чтобы значения обобщенного многочлена и его производных до определенного порядка в узлах совпадали с соотв-щими значениями функции и ее производных:

.

Ограничимся рассмотрением здесь случая, когда , то есть, общей задачей интерполирования алгебраическими многочленами. Для функциии набора попарно неравных узлов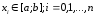требуется построить многочлен, удовлетворяющий условиям

. (1)

Рассмотрим разность , где- интерпол-ный многочлен Лагранжа дляпо узлам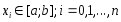. Так какпри, то. (2)

Исходная задача сведена к построению многочлена .

Продиф-руем равенство (2): . Для узлов, в которых заданы значения производнойотсюда имеем. (3)

Дифференцируя равенство (2) дважды, получим

Отсюда для узлов , в которых заданы значения производной, имеем

Далее, приходим к задаче построения многочлена степени, удовл. усл.. (4)

Для построения многочлена по условиям (4) применяем тот же прием, что и при построении многочлена по условиям (1). Повторяя процесс, приходим к задаче построения интерполяционного многочлена по его значениям в узлах, где в (1) задавались значения старшей производной. Последняя задача решается единственным образом и, следовательно, искомый многочлен имеет степень и является единственным.

Многочлен , удовлетворяющий условиям (1), называют многочленом Эрмита для функциипо набору попарно неравных узловс соответствующими кратностями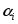узлов.

Проведем построение многочлена Эрмита для случая, когда все узлы имеют одинаковую кратность, равную двум. Условия (1) при этом принимают вид

. (5)

Используя формулы (2) и (3), получим ;

.

Т.о., построен искомый интерпол-ный многочлен Эрмита

. (6)

Проведем в выражении (6) алгебраические преобразования. Учтем, что 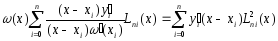и

Тогда формула (6) примет вид

(7)

Рассмотрим выражение в фигурных скобках . Это многочлен степени. При этом

Следовательно, рассматриваемый многочлен представляется в виде . (8)

Полагая в (8) , имееми. Из условия

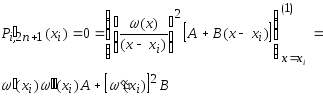находим

. Подставляя полученные выражения коэффициентов в (8), имеем

.

Заменим в (7) многочлен в фигурных скобках найденным выражением, тогда для многочлена Эрмита с узлами кратности 2 получим окончательное выражение

. (9)

12. Некорректность задачи численного диф-я в пр-ве ℂ.Пусть функция задана на отрезкетаблицей значенийи надо найти приближенное значение ее производной в некоторой точке этого отрезка.

Решение поставленной задачи можно провести с использованием интерполяционного многочлена Лагранжа порядкаn, который приближает функцию с погрешностью . Дифференцируя равенство,(1) m раз имеем погрешность .(2)

Таким образом, производная многочлена приближает производную функциис погрешностью, т.е., приближенное равенство(3) имеет погрешность .

_{Покажем, что в общем случае малая разность между двумя функциями на отрезке еще не означает, что малой будет и разность их производных на этом отрезке. В качестве примера рассмотрим функции} ℂ и . Найдем отклонениеот. Расстояние между этими функциями в пространствеℂ равно

а расстояние между их производными в этом пр-ве 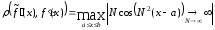. Некорректность в пространствеℂ задачи численного дифференцирования заключается в том, что из сходимости в этом пространстве последовательности функций не следует, что последовательность производных этих функций также будет сходиться.

Примеры формул численного дифференцирования

В качестве примера рассмотрим использование для интерполирования в начале таблицы интерполяционного многочлена Ньютона:

.

Дифференцируя приближенное равенство будем иметь:

_.В случае 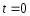формула приобретает вид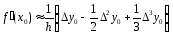. Для второй производной получаем соответственно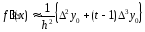и.

Третья производная многочлена третьей степени является константой .

При неравноотстоящих узлах для построения формул численного дифференцирования используются интерполяционный многочлен Лагранжа

и интерполяционная формула Ньютона с разделенными разностями

.