1.Источники и классификация погрешностей. Неустранимая и вычислительная погрешность.

В вычислительной математике, как правило, рассматривается решение корректно поставленных задач. Это значит, что исходная задача имеет единственное решение, которое в некоторой области непрерывно зависит от исходных данных задачи. Другими словами, при малой погрешности в задании исходных данных решение корректно поставленной задачи также изменяется на малую величину. На практике значения почти всех величин задаются и определяются приближенно. Это обстоятельство для вычислительной математики имеет исключительную важность. Решение каждой задачи должно быть получено с точностью, позволяющей использовать его на практике. Провести решение задачи нужно так, чтобы погрешность полученного решения не превышала допустимую. Рассмотрим несколько подробнее источники погрешностей на конкретном примере. Пусть требуется вычислить площадь фигуры, состоящей из прямоугольного треугольника и полукруга, построенного на одном из катетов как на диаметре. При этом заданы значения угла 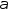и гипотенузы, полученные в результате измерения. Точные значения исходных величин обозначим соответственн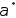ои . 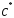Таким образом, точное значение площади выражается формулой .

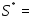
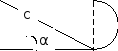
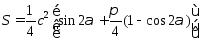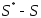Значение площади через заданные значения исходных величин определяется выражением . Разностьназывают неустранимой погрешностью. Эта погрешность обусловлена неточным заданием исходных данных. Чтобы уменьшить неустранимую погрешность, нужно более точно измерить значения исходных величин, а это входит в обязанности заказчика, а не математика, решающего задачу. Для вычисления значений тригонометрических функций воспользуемся их разложениями в ряд Тэйлора, тогда придем к равенству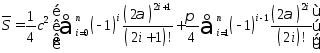. 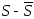Разностьназывают погрешностью метода. Погрешность метода можно сделать достаточно малой. В нашем примере математику для этого нужно взять в разложениях достаточно большое значение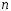. Исходные данные и иррациональные числа округляются при вводе в вычислительную машину, округляются также промежуточные и окончательные результаты. Фактически вычисленное значение площади обозначим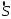. Разностьназывают вычислительной погрешностью. Уменьшить вычислительную погрешность можно за счет использования ЭВМ с большей разрядной сеткой, а также за счет программирования операций над числами с большой разрядностью. Полная погрешностьскладывается из трех указанных видов погрешности:.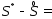

Неустранимая погрешность. Обозначим 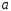– приближенное значение величины,- ее точное значение. Погрешность приближенной величины определим равенством.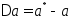

Если дробь приближается числом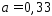, то для погрешности такого приближения получим.

На практике редко можно получить точное значение погрешности приближенной величины. Поэтому используется понятие абсолютной погрешности. Абсолютная погрешность определяется неравенством .

Конечно, стремятся найти как можно меньшее значение абсолютной погрешности , удовлетворяющее указанному неравенству. Например, в случае приближения иррационального числачислом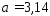в качестве абсолютной погрешности можно взять или 0.002 или 0.0016, но не 2 или 3, хотя под определение абсолютной погрешности последние числа и подходят.

Величину 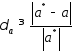называют относительной погрешностью приближенного числа. Если, то в качестве относительной погрешности можно взять число.

Значащими цифрами числа называют все его ненулевые цифры и нули, которые находятся между значащими цифрами или являются представителями сохраненного десятичного разряда.

Значащая цифра приближенного числа называется верной, если абсолютная погрешность числа не превосходит половины единицы разряда, в котором эта цифра находится.

Замечание 1. Абсолютные и относительные погрешности записывают с точностью до одной или двух значащих цифр.

Замечание 2. Абсолютные и относительные погрешности округляют только с избытком.

Рассмотрим вопрос оценки неустранимой погрешности решения задачи на примере вычисления значения функции 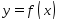по заданному значению аргумента. Значение аргумента задано с абсолютной погрешностью. Требуется оценить абсолютную погрешность.

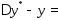
Используя формулу конечных приращений Лагранжа, получим . Отсюда имеем неравенство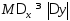, где. Таким образом, можно положить.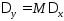

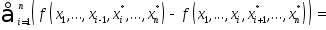
Аналогично оценивается неустранимая погрешность в случае функции нескольких переменных . Имеем. Отсюда для абсолютной погрешности функции получаем искомое выражени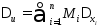е, где,.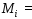

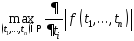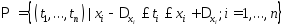Вычислительная погрешность.

Пусть квадратное уравнение решается с помощью вычислительного устройства, которое выполняет арифметические операции с точностью до четырех значащих десятичных цифр. Рассмотрим вычисление меньшего корня в соответствии с равенством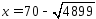. При извлечении корня на устройстве получится. При вычитании на устройстве получится 70.00-69.99=0.01. Таким образом, окончательный результат получается с точностью до одной значащей цифры.

Изменим алгоритм вычислений в соответствии с выражением .

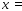
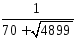Результат первого действия 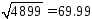остается таким же. Результат второго действия 70.00+69.99=140.0 проходит с округлением до четырех значащих цифр. В третьем действии получается окончательный результат 1/140.0=0.007143 с точностью до четырех значащих цифр. Данный пример показывает, что избранный алгоритм вычислений может существенно влиять на величину вычислительной погрешности.

В качестве второго примера рассмотрим вычисление суммы чисел на том же вычислительном устройстве: x = 1.23+9.374+0.0046+0.0039+0.0141. Пусть проводится сложение слева направо: 1.23+9.374=10.60; 10.60+0.0046=10.60; 10.60+0.0039=10.60; 10.60+0.0141=10.61.

А теперь проведем на устройстве сложение тех же чисел в порядке справо налево: 0.0141+0.0039=0.0180; 0.018+0.0046=0.0226; 0.0226+9.374=9.397; 9.397+1.23=10.63. Как видите, при вычислениях на реальном устройстве сумма слагаемых зависит от их порядка (суммирования).