43. Метод бисекции и простой итерации решения уравнений с одним неизвестным.

Уравнение с одним неизвестным имеет следующий общий вид , (1), где– функция, заданная на всей числовой оси или на конечном ее отрезке.

Теорема1. Если функция непрерывна на отрезкеи принимает на концах этого отрезка значения разных знаков, то уравнение (1) имеет внутри отрезка хотя бы один корень.

Доказательство. Обозначим . Пусть построены отрезки, удовлетворяющие условиям:

1) ; 2); 3).

Рассмотрим построение очередного отрезка Найдем середину отрезка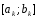:(2) и вычислим. Если, то утверждение теоремы справедливо.

Пусть . Положим, еслиив противном случае. Очевидно выполнение равенства(3). Так как последовательностьне убывает и ограничена сверху, то она имеет предел. Из (3) следует, что и. Поскольку, то. Отсюда и из непрерывности функции получаем. Теорема доказана. Метод решения уравнения (1), построенный при доказательстве теоремы называют методом бисекции или методом половинного деления отрезка.

Метод простой итерации.

Пусть на отрезке задано уравнение в виде. (4)

Метод простой итерации для уравнения (4) имеет расчетную формулу . (5)

Теорема2. Пусть уравнение (4) имеет корень и существует такое, что на отрезкепроизводная функциисуществует, непрерывна и по модулю строго меньше единицы:. Тогда метод простой итерации (5) сходится при.

Доказательство. Очевидно, отрезок является полным метрическим пространством. Длявыполняетсяи, по формуле конечных приращений Лагранжа, получается

.

Это значит, что функция 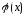отображает отрезокв себя.

Для справедливо

.

Это значит, что отображение функции на отрезкесжатое. Таким образом, справедливость данной теоремы следует из принципа сжатых отображений. Теорема доказана.

44. Методы хорд и касательных как частные случаи метода простой итерации.

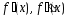Квадратический характер сходимости метода касательных (Ньютона). Пусть на отрезке задано уравнение в виде. (1) Будем считать, что на отрезкеуравнение (1) имеет кореньи производныенепрерывны на отрезке и сохраняют знак. Введем в рассмотрение функцию, которая непрерывна наи не обращается на нем в нуль. При этих условиях уравнение(2) будет равносильно на отрезкеуравнению (1). Уравнение (2) имеет вид, где. Возьмем. Тогда уравнение (2) приобретает вид. (3)

Запишем расчетные формулы метода простой итерации для уравнения (3) . (4)

Построенный метод решения уравнения (1) с расчетными формулами (4) называют методом хорд.

Исследуем сходимость метода хорд. Проводя дифференцирование в (3), получаем . (5) Используя разложение в ряд Тейлора, имеем. Положив в последнем равенстве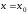, выразим остаточный член формулы Тейлора. После подстановки в (5) и применении к знаменателю в (5) формулу конечных приращений Лагранжа, получим

.

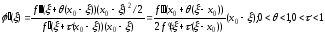Отсюда имеем оценку , (6), где. Оценка (6) показывает, что если взятьдостаточно близким к корню, то будет выполняться неравенство. В силу непрерывности производной, существует- окрестность точкиотрезка, где выполняются условия теоремы о сходимости метода простой итерации.

Возьмем теперь . Тогда уравнение (2) приобретает вид. (7)

Запишем расчетные формулы метода простой итерации для уравнения (7) (8)

Построен. метод решения ур-я с расчетными ф-ми (8) наз. методом Ньютона (касательных). Исследуем сх-ть метода Ньютона. Проводя диф-е в (7) получаем . Метод Ньютона имеет квадратич. хар-р сх-ти. Действительно, из (8) имеем. (9) Используя разложение в ряд Тэйлоранаходим. Заменяя в (9) правую часть полученным выражением, приходим к формулеи оценке, где.