30. Метод Гаусса решения системы линейных ур-ний.

Рассм. сис-му лин. алгебр. уравнений Ax=b (1), где . Будем предполагать, чтоdet(A)≠0, т.е. система (1) однозначно разрешима при любой правой части. Перепишем (1) в развернутом виде (2). Идея метода Гаусса в приведении матрицы А в (1) к треугольному виду. После этого нахождение вектора x не будет составлять труда. На (k-1)-ом шаге метода Гаусса система (2) приводится к виду:, (3)

. (4) На k-ом шаге метода Гаусса обрабатыв. только подсистема (4). Вначале приводим 1-ый коэффициент 1-ого уравнения в (4) к единице, т.е. , коэфф-ты которого вычис. через коэффициенты системы (4) по расчетной формуле

(5). Далее из всех уравнений подсистема (4) начиная со 2-го исключает неизвестную ,т.е. все ур-ния подсистемы (4) начинаясо 2-го приводим к виду

Коэффициенты системы рассчитываются по формуле (6)

На этом заканчивается k-ый шаг метода и начин. очередной k+1 шаг. Указанные шаги повторяются до тех пор, пока исходная система (2) не будет приведена к виду:

,(7) (8). На этом заканчивается прямой ход метода Гаусса и начинается обратный. Из последнего ур-ния(8)Далее, двигаясь по системе снизу-вверх находим

Замечание1. При реализации вычислений по ф-лам (5) (6) прдполагаем . В случае нарушения этого услов необходимо соответств образом переставить ур-ния в (4).Замечание2. В ходе вычислен по (5) определитель м-цы А делится на величину . Определит системы (7)(8) очевидно равен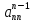поэтому.

31. - Разложение квадратных матриц.

Пусть данная квадратная матрица. Будем строить разложение этой матрицы в виде: (1), где - нижняя (левая) треугольная матрица, - верхняя (правая) треугольна матрица.

Теорема: Пусть все главные миноры матрицы отличны от, тогда (1) существует.

При этом, если диагональ одной из матриц или фиксированы, то такое разложение единственное.

Вместо доказательства укажем способ построения разложения (1) . Зафиксируем элементы главной диагонали матрицы положив их равными. Матричному равенству (1) поставим в соответствие равенство:

(2)

Выполнив умножение в левой части (2) получим систему уравнений относительно неизвестных ,.

(3)

Специфика данной системы позволяет решать её следующим образом: из 1 строки в (3) находим ,. Из оставшейся части 1-ого столбца находим,,. Далее, из оставшейся части 2-ой строки находим,. Из оставшейся части 2-ого столбца находим,, и т.д. Последним определяем элемент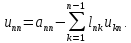

Указанный процесс решения системы (3) можно описать посредством двух формул: 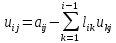,(4)

, (5)

При практическом счёте необходимо вовремя переключаться с формулы (4) на формулу (5) в соответствии с указанной выше последовательностью. При выполнении условий теоремы формула (5):. Действительно,и т.д.

Замечание: Разложение (1) всегда осуществимо, если матрица. А является матрицей с диагональным преобразованием, т.е. для такой матрицы выполняется ,

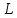Рассмотрим систему линейных алгебраических уравнений (6). Применим к матрице-разложение. В итоге, будем иметь(7)

Систему (7) представим в виде двух систем (8)

Поскольку матрицы итреугольные, то решения каждой из подсистем (8) идентично обратному ходу метода Гаусса.