24. Многочлены наилучших равномерных приближений. Примеры.

Рассмотрим пр-во - непрерывных наф-ий. Пусть. Будем рассматривать задачу аппроксимации ф-ииf многочленом степениn.Если степень n не фиксир., то ф-ию f можно с любой точностью приблизить к соответствующим многочленам более точно справедлива следующая теорема.

Теорема Веерштрасса. и что

Если число n –фиксировано, то ф-ию f уже нельзя приблизить с любой точностью к многочлену однако для любой ф-циистепениn, такой что , гдеберётся по всевозможным многочленам степениn. Такой многочлен наз. многочленом наилучшего равномерного приближения или Чебышевским приближением. Отметим, что не существует общего алгоритма построения мног.однако для построения этого многочлена можно использовать след. утв.:

Теорема Чебышева:Для того, чтобы многочлен степени n был многочленом наилучшего равномерного приближения для ф-ии f необх. и достат., чтобы насуществовали по крайней мереn+2 точки в которыхгде.

Другими словами, теорема говорит о том, что в точках поочерёдное отклонение ф-ции f от многочленадостигает наиб. значений . При этом точкиназ. точками Чебышевского альтернанса.

Пример1.Будем аппроксимировать ф-ию f многочлена нулевой степени 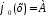. Положим.

Положим . Покажем , что в этом случае многочленесть многочлен наилучшего равномерного приближения. Имеем

А точки в которых f(x)=m и f(x)=М образуют Чебышевский альтернанс.

Пример2.Пусть и является выпуклой . Будем аппроксимировать ф-цию f многочленом.

Составим разность Пусть С – точка экстремума ф-ции(очевидно, что такая точка существует, причём). Потребуем, чтобы точкиа,с,в в указанном порядке образ. Чебышевский альтернанс. В этом случае будем иметь две системы уравнений:

Относительно неизвестных Е, с, .Заметим, что в данных системах через Е обозначено, а 4-ое уравнение каждой из систем есть условие того, что точка С – точка экстремума ф-ции.

25. Наилучшие приближения в линейном нормированном пространстве.

Пусть 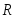- линейное нормированное пространство и в нем задана последовательность линейно независимых элементов. Рассмотрим множество линейных комбинаций

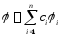, где - числовые коэффициенты.

Будем аппроксимировать ф-ию f ф-ей т.о., что(1)

При этом наз-ть эл-ом наилучшего приближения.

Теорема. В ЛНП элемент наилучшего приближения всегда существует.

Д-во. Обозначим 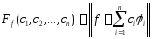. Покажем, что функциянепрерывно зависит от своих аргументов.

Для приращения функции

используя для нормы аксиому треугольника, имеем

(2). Отсюда получаем оценку:

, из которой следует непрерывность ф-ии .

На единичной сфере , которая является замкнутым ограниченным множеством, непрерывная функцияпринимает свое минимальное значение. Обозначим его через. В силу аксиомы тождества для нормы и линейной независимости элементов, должно выполняться. В случае произвольного набора коэффициентов имеем

. (3) Выберем число . Ф-иянепрерывна на шаре, поэтому достигает на нём своей нижней грани

Заметим, что (4) . Вне шара, т.е. при с учётом (3) и (4) имеем оценку:Показали, что на шареф-иядостигает своего минимума, а вне шаравып-ся.

ЛНП наз-ся строго нормированным, если из условия следует, что, гдечисло.