46. Метод Лобачевского решения алгебраических уравнений.

В соответствии с основной теоремой алгебры имеет место тождество , (1). где- действительные и комплексные корни многочлена. Отсюда получаем соотношения между корнями и коэффициентами многочлена:

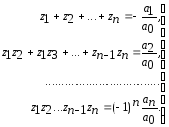(2)

Если все корни многочлена действительны и сильно отличаются по абсолютной величине между собой:

, (3), то последовательно из уравнений системы (2) получим:

(3)

Лобачевский предложил следующий способ получения из данного уравнения нового уравнения, корни которого равны квадратам корней исходного уравнения. Заменяя в тождестве (1)на, получим

(4). Очевидно, корни многочлена отличаются от соответствующих корней многочленатолько множителем (-1). Из тождеств (1) и (4) имеем

.

Таким образом, получается многочлен , корни кот. равны квадратам корней многочлена, умноженным на (-1). Коэффициенты многочленаопределяются из тождества

:

, (5), где при.

Полагая , получаем расчетные формулы

(6) для последовательного построения многочленов с корнями. Процесс расчетов по формулам (6) называют квадрированием.

Вычисления по формулам (6) прекращают при достижении итерации j, для которой в пределах заданной точности при всех k = 1, 2, …,n будут выполняться приближенные равенства . После этого в случае всех действительных простых и различных по модулю корней вычисляют искомые корни.

Знак корней определяют непосредственной подстановкой в исходное уравнение.

47. Методы простой итерации и Зейделя решения системы нелинейных уравнений.

Метод простой итерации

Рассмотрим систему нелинейных уравнений, заданную в виде , (1), где–n-вектор-функция, заданная в n-мерном векторном пространстве или на некотором его множестве. Решение уравнения (1) равносильно нахождению неподвижной точки оператора . Метод простой итерации решения системы (1) имеет расчетную формулу(2).

Достаточные условия сходимости метода простой итерации (2) дает следующая

Теорема. Пусть система (1) имеет решение и выполнены условия:

1) функции определены и непрерывно дифференцируемы в области

2) и удовлетворяют там неравенствам

, (i=1,2,…,n).

Тогда при любом начальном приближении метод простой итерации (2) сходится к решению.

Доказательство. Очевидно, n-мерный параллелепипед П является полным метрическим пространством. Покажем, что оператор отображает его в себя. Определим посредством кубической нормы расстояние между двумя точками вn-мерном пространстве. Используя теорему о среднем для функции сn аргументами имеем , где.Отсюда, учитывая условие 2) теоремы получимпри. Теперь покажем, что отображение с функциейявляется сжимающим в области П. Для любыхвыполняется

Здесь промежуточные точки определяются аналогично точкам. Таким образом, в данном случае выполняются все условия принципа сжатых отображений в полном метрическом пространстве П. Отсюда следует справедливость утверждения теоремы и единственность решения системы (1) в П. Теорема доказана.

Погрешность последовательных приближений в методе простых итераций (2) при выполнении условий теоремы стремится к нулю не хуже, чем члены геометрической погрешности со знаменателем . Это непосредственно следует из проведенных ниже преобразований.

Здесь .

Метод Зейделя для решения нелинейной системы (1) имеет расчетную формулу. (3).

Достаточные условия сходимости метода Зейделя (3) такие же, как и сформулированные в теореме достаточные условия сходимости метода простой итерации (2). Действительно, поскольку

где ,

то посл-но получаем

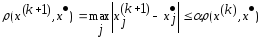Отсюда имеем . Утверждение доказано.