4.6. Пересечение прямой с плоскостью.

Задача на пересечение прямой линии с плоскостью является также одной из основных задач начертательной геометрии. Она входит составной частью в решения различных задач по всем разделам курса.

Пример: Определить точку пересечения прямой ЕF с плоскостью β (рис.32).

Порядок решения задачи (алгоритм решения):

1. Провести через данную прямую вспомогательную плоскость (удобнее проецирующую);

2. Построить линию пересечения данной и вспомогательной плоскостей 1-2= β ∩ α ;

3. Отметить искомую точку на пересечении данной прямой с линией пересечения плоскостей. К=(1-2)∩ ЕF К=ЕF∩ β (рис.32а)

Плоскость β (АВСD) пересекается с прямой ЕF (рис.32б).

1. Через прямую ЕF провести плоскость (α П₂); α₂ ≡Е₂F ₂;

2. Построить линию пересечения плоскостей β и α: (1 - 2) =( β ∩ α);

3. Отметить точку К пересечения линии EF и (1 - 2): К = (ЕF) ∩ (1 - 2); К₁ = (Е₁ F₁) ∩ (1₁ - 2₁).

Решение задачи завершается определением видимых участков прямой относительно плоскости β, считая ее непрозрачной.

4.7. Вопросы для самопроверки.

1. В каком случае прямая параллельна плоскости?

2. Назовите признак параллельности плоскостей.

3. Назовите признак перпендикулярности прямой плоскости.

4. Сформулируйте условие перпендикулярности двух плоскостей.

5. Как построить линию пересечения плоскостей?

6. Какова последовательность построения точки пересечения прямой с плоскостью общего положения.

5. Лекция 5. Способы преобразования проекций.

5.1. Общие положения.

Способы преобразования проекций предназначены для решения метрических задач, связанных с определением действительных размеров и формы изображаемых на эпюре геометрических объектов.

Преобразование проекций имеет целью привести данные геометрические образы в некоторое частное положение относительно плоскостей проекций. Новое положение выбирается так, чтобы упростилось решение поставленной задачи.

Изменять положение заданных образов по отношению к плоскостям проекций можно двумя путями:

1. геометрический объект в пространстве остается неподвижным, изменяет положение аппарат проецирования (способ замены плоскостей проекций);

2. геометрический объект изменяет свое положение в пространстве, аппарат проецирования неподвижен (способы вращения, способ перемещения).

5.2. Способ замены плоскостей проекций.

Сущность способа заключается в том, что при неизменном положении объекта в пространстве производится замена данной системы плоскостей новой системой взаимно - перпендикулярных плоскостей. При переходе к новой системе одну из плоскостей проекций заменяют новой плоскостью так, чтобы заданный геометрический элемент (прямая, плоскость …) занял частное положение и проецировался без искажения на новую плоскость проекций.

При этом должны соблюдаться два условия:

1. вновь вводимая плоскость должна быть перпендикулярна оставшейся плоскости;

2. направление проецирования к новой плоскости должно быть ортогональ­ным.

В системе П₁ и П₂ задана точка А. (рис. 33).

Рис. 33

Плоскость П₂ заменяем на плоскость П₄.

П₄П₁, П₄ ∩ П₁ = X_1,4.

Точку А ортогонально спроецируем на плоскость П₄.

Плоскость П₁ является общей для старой и новой систем, и поэтому координата Z точки сохраняется.

A₄A_X1,4 = A₂A_X1,2=Z_A

Для получения эпюра плоскость П₄ вращением вокруг оси Х_1,4 совмещается с плоскостью П₁.

Порядок построения новой проекции точки (рис. 34).

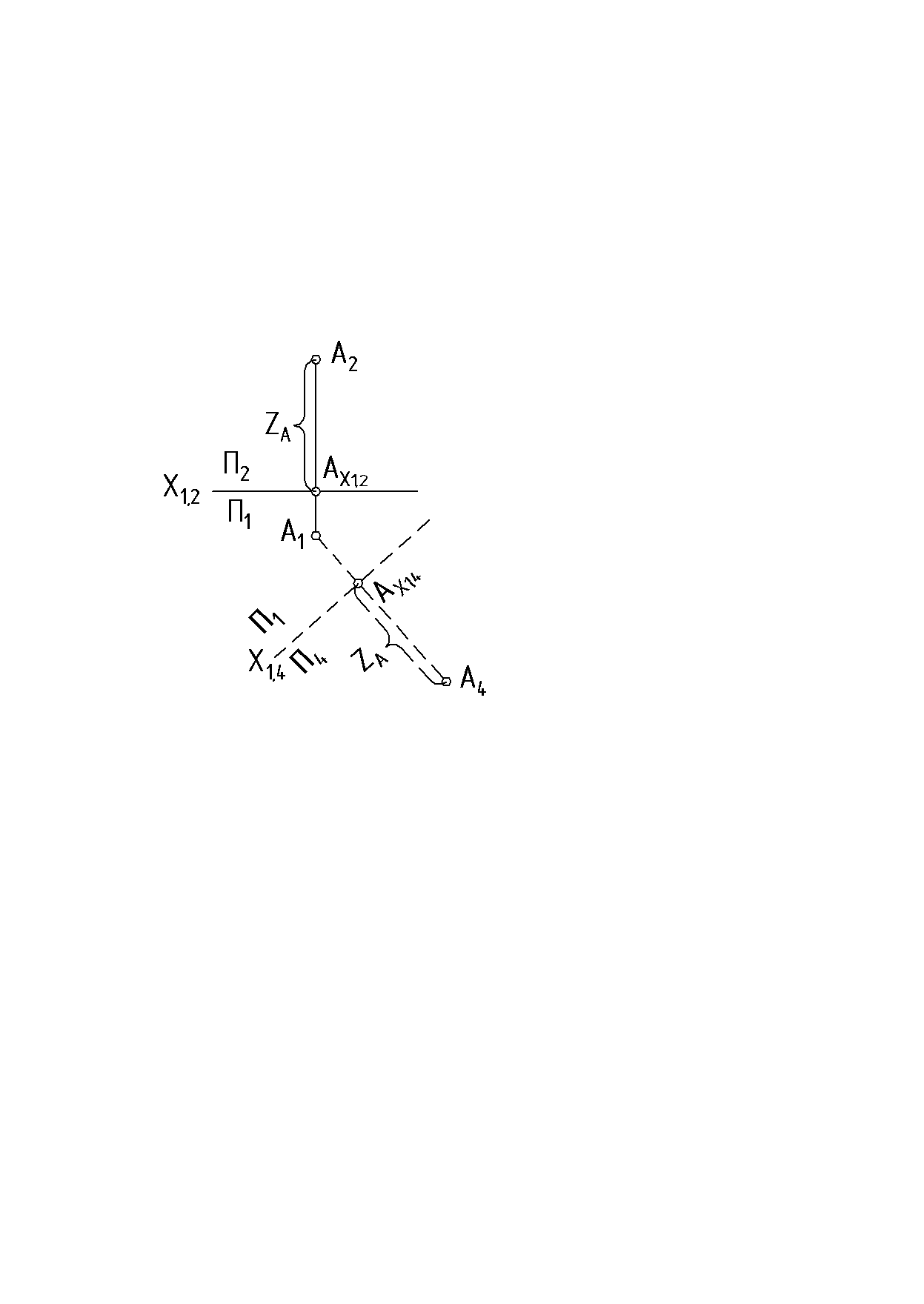
Рис. 34

1. Проводим новую ось проекции Х_1,4

2. Проводим линию связи между оставшейся проекцией точки и новой (А₁А₄)  Х_1,4.

3. Измеряем координату Z_A точки на замененной плоскости П₂ и откладываем ее на новой линии связи от новой оси Х_1,4 до новой проекции А_4.