
Sistemy_shirokopolosnoy_radiosvyazi_2009
.pdf
4.11. Рекуррентный алгоритм скользящего корреляционного декодирования 155
Найдем оценку удельных коэффициентов аппаратурной сложности арифметического устройства СКД-декодера двоичных циклических кодов. Для этого установим связь в аналитическом виде между координатами zi , i 0, n 1 , вектора Z CY при рекуррентном скользящем режиме корреляционного декодирования.
Принятое колебание y(t) — смесь сигнала с шумом — представим для каждого элемента разрешения по времени с номером k с помощью его n1 текущих отсчетов как вектор-столбец
Y (k) = {y(k)}, |
i = |
|
, k = |
|
. |
(4.71) |
||
0, n -1 |
0, n -n |
|||||||
i |
|
|
|
|
|
1 |
|
|
Причем отсчеты |
|
|
|
|
|
|
|
|
y |
k j |
, |
при |
(k j) n |
|
|
|
|
|
|
|
1 |
, |
|
(4.72) |
||
y(jk) |
|
|
при |
(k j) n |
|
|||
0, |
|
|
|
|
||||
|
|
|
|
1 |
|
|
||
где n1 — общее число элементов разрешения по времени. В общем |
||
случае n1 n . |
|
|
Элементы вектора корреляции Z(k) определяются соотношением |
||
n 1 |
|
|
zi(k) yk jci, j , |
i 0, n 1 , |
(4.73) |
j 0
для каждого k 0, n1 n .
Одно из основных свойств матрицы-циркулянта состоит в том,
что для произвольных целых чисел i, j, |
справедливо равенство |
ci, j ci , j , |
(4.74) |
где значения индексов редуцируются по модулю n .
Найдем связь в аналитическом виде между координатами векторов Z(k) и Z(k 1) . Для этого представим выражение (4.73) с учетом (4.70) в виде
n 2 |
|
|
|
zi(k) yk jci, j |
yk n 1ci,n 1, |
i 0, n 1 , |
(4.75) |
j 0
а выражение для -й координаты вектора Z(k 1)
n 1 |
|
|
|
z(k 1) yk 1 j c , j yk 1 c ,0 , |
|
|
, |
0, n 1 |
|||
j 1 |
|
|
|

156 Глава 4 | Системы бинарных фазоманипулированных сигналов. БФМ-сигналы
или изменяя пределы суммирования
n 2 |
|
z(k 1) yk j c , j 1 yk 1 c ,0 . |
(4.76) |
j 0
Сопоставляя выражения сумм в правых частях соотношений (4.75) и (4.76), находим, что при значении i 1 эти суммы тождественно равны и, следовательно, справедливо рекуррентное соотношение для каждого k 1, 2, 3
z(k) |
z(k 1) |
y |
k n |
1 |
c |
|
k 1, i 1 |
, i |
0, n 1 |
, |
(4.77) |
i |
i 1 |
|
i, n 1 |
|
|
|
|
|
|||
где величины |
k 1, i 1 |
yk 1 ci 1,0 |
представляют собой вычитаемые |
||||||||
вклады от ранее поступившего точно n тактов назад отсчета yk 1 . Соотношение (4.77) представляет собой, по существу, рекуррент-
ный алгоритм вычисления круговых сверток (корреляций) произвольных циклических кодов максимальной длины при отсутствии синхронизации декодера по кодовым словам. Анализ алгоритма (4.77) при условии синхронизации декодера и, следовательно, при значении n1 n , т. е. когда отсутствует влияние вычитаемых вкладов
yk 1, i 1 , позволяет непосредственно найти значения его параметров: |
|||
QA n, |
QM n . Поскольку в данном случае |
J n , то аппаратур- |
|
ная сложность АУ СКД-декодера |
|
|
|
|
A 1 , |
M 1 |
(4.78) |
для произвольных двоичных кодов максимальной длины.
Заметим, что АУ корреляционного декодера кодов максимальной длины с максимальным уровнем параллелизма работы на основе алгоритма Уолша-Адамара характеризуется такими значениями коэффициентов сложности [64]:
A log2 n k , |
M 1 . |
(4.79) |
Рассмотрим пример построения СКД-декодера для кода максимальной длины, заданного первообразным неприводимым над полем GF (2) полиномом f (x) x3 x 1. Кодовая матрица-циркулянт этого кода (в знаковой форме) имеет вид

4.11. Рекуррентный алгоритм скользящего корреляционного декодирования 157
c0c6c5
C c4c3c2
c1
c1 |
c2 |
c3 |
c4 |
c5 |
c0 |
c1 |
c2 |
c3 |
c4 |
c6 |
c0 |
c1 |
c2 |
c3 |
c5 |
c6 |
c0 |
c1 |
c2 |
c4 |
c5 |
c6 |
c0 |
c1 |
c3 |
c4 |
c5 |
c6 |
c0 |
c2 |
c3 |
c4 |
c5 |
c6 |
c |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|||||
5 |
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|||||
4 |
|
|
|
|
|
|
|
|
|
, |
c |
|
|
|
|||||||
3 |
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|||||
0 |
|
|
|
|
|
|
|
|
|
|
при этом схема СКД-декодера (при наличии синхронизации) приведена на рис. 4.13,
Рис. 4.13. Схема СКД-декодера циклического кода длины n 7
где для простоты устройство синхронизации не показано. Нетрудно непосредственно убедиться, что эта схема действительно вычисляет за каждые n тактов работы полный вектор корреляции Z , после чего решающее устройство производит отбор максимальной координаты и обнуление регистра памяти, т. е. восстановление нулевых начальных условий работы декодера, что, по сути, устраняет влияние вычитаемых вкладов yk 1, i 1 в алгоритме (4.77).
Приведенный алгоритм легко распространяется на случай декодирования произвольных кодов Боуза-Чоудхури-Хоквингема (БЧХ).

158 Глава 4 | Системы бинарных фазоманипулированных сигналов. БФМ-сигналы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.9 |
|
|
|
|
Кодовые слова (15,5) кода БЧХ |
|
|
|
|
Веса |
||||||||
|
|
|
|
|
|
|
|
кодовых слов |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
+ + + + + + + + + + + + + + + |
ü |
w 0 |
||||||||||||||
ï |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
2. |
+ + + + - + - + + - - + - - - |
ï |
|
||||||||||||||
ï |
w 7 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
3. |
- + + + + - + - + + - - + - - |
ï |
|
||||||||||||||
ï |
w 8 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
4. |
- - + + + + - + - + + - - + - |
ï |
|
||||||||||||||
ï |
w 15 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
5. |
- - - + + + + - + - + + - - + |
ï |
|
||||||||||||||
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
6. |
+ - - - + + + + - + - + + - - |
ï |
|
||||||||||||||
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
7. |
- + - - - + + + + - + - + + - |
ï |
|
||||||||||||||
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
8. |
- - + - - - + + + + - + - + + |
ï |
|
||||||||||||||
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
9. |
+ - - + - - - + + + + - + - + |
ï |
|
||||||||||||||
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
10. |
+ |
+ |
- |
- |
+ |
- |
- |
- |
+ |
+ |
+ |
+ |
- |
+ |
- |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
11. |
- |
+ |
+ |
- |
- |
+ |
- |
- |
- |
+ |
+ |
+ |
+ |
- |
+ |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
12. |
+ |
- |
+ |
+ |
- |
- |
+ |
- |
- |
- |
+ |
+ |
+ |
+ |
- |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
13. |
- |
+ |
- |
+ |
+ |
- |
- |
+ |
- |
- |
- |
+ |
+ |
+ |
+ |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
14. |
+ |
- |
+ |
- |
+ |
+ |
- |
- |
+ |
- |
- |
- |
+ |
+ |
+ |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
15. |
+ |
+ |
- |
+ |
- |
+ |
+ |
- |
- |
+ |
- |
- |
- |
+ |
+ |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
16. |
+ |
+ |
+ |
- |
+ |
- |
+ |
+ |
- |
- |
+ |
- |
- |
- |
+ |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ý |
|
17. |
- |
- |
- |
- |
+ |
- |
+ |
- |
- |
+ |
+ |
- |
+ |
+ |
+ |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
18. |
+ |
- |
- |
- |
- |
+ |
- |
+ |
- |
- |
+ |
+ |
- |
+ |
+ |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
19. |
+ |
+ |
- |
- |
- |
- |
+ |
- |
+ |
- |
- |
+ |
+ |
- |
+ |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
20. |
+ |
+ |
+ |
- |
- |
- |
- |
+ |
- |
+ |
- |
- |
+ |
+ |
- |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
21. |
- |
+ |
+ |
+ |
- |
- |
- |
- |
+ |
- |
+ |
- |
- |
+ |
+ |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
22. |
+ |
- |
+ |
+ |
+ |
- |
- |
- |
- |
+ |
- |
+ |
- |
- |
+ |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
23. |
+ |
+ |
- |
+ |
+ |
+ |
- |
- |
- |
- |
+ |
- |
+ |
- |
- |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
24. |
- |
+ |
+ |
- |
+ |
+ |
+ |
- |
- |
- |
- |
+ |
- |
+ |
- |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
25. |
- |
- |
+ |
+ |
- |
+ |
+ |
+ |
- |
- |
- |
- |
+ |
- |
+ |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
26. |
+ |
- |
- |
+ |
+ |
- |
+ |
+ |
+ |
- |
- |
- |
- |
+ |
- |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
27. |
- |
+ |
- |
- |
+ |
+ |
- |
+ |
+ |
+ |
- |
- |
- |
- |
+ |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
28. |
+ |
- |
+ |
- |
- |
+ |
+ |
- |
+ |
+ |
+ |
- |
- |
- |
- |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
29. |
- |
+ |
- |
+ |
- |
- |
+ |
+ |
- |
+ |
+ |
+ |
- |
- |
- |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
30. |
- |
- |
+ |
- |
+ |
- |
- |
+ |
+ |
- |
+ |
+ |
+ |
- |
- |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
31. |
- |
- |
- |
+ |
- |
+ |
- |
- |
+ |
+ |
- |
+ |
+ |
+ |
- |
ï |
|
ï |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
32. |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
ï |
|
- þï |
|
||||||||||||||||
4.11. Рекуррентный алгоритм скользящего корреляционного декодирования 159
Построим схему СКД-декодера, например (15,5) кода БЧХ. Все кодовые слова (15,5) кода БЧХ в знаковой форме (+ 0, — 1), построенные в соответствии с методикой [3], а также спектры их весов, построены в табл. 4.9.
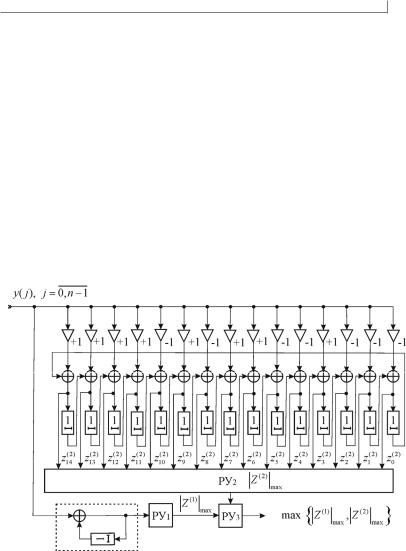
Из анализа данных табл. 4.9 видно, что для данного кода одна половина кодовых слов обратна (инверсна) другой ее половине, следовательно, при когерентном приеме соответствующие векторы корреляции будут отличаться только знаком, что позволяет дополнительно уменьшить значения удельных коэффициентов (4.78) аппаратурной сложности декодера — рис. 4.14.
Поскольку (15,5) код БЧХ полностью определяется двумя порождающими кодовыми словами, которые обозначены под номерами 1 и 2 в табл. 4.9, поэтому полная схема рекуррентного декодирования состоит из двух парциальных декодеров, как это и показано на рис. 4.14.
Рис. 4.14. Схема СКД-декодера (15,5) -кода БЧХ
Первый парциальный декодер, обведенный пунктиром на рис. 4.14, состоит из рециркулятора-накопителя и решающего устройства РУ1 для отбора максимума, предназначен для декодирования принятого

160 Глава 4 | Системы бинарных фазоманипулированных сигналов. БФМ-сигналы
слова Y по кодовым словам 1 и 32 путем вычисления одномерного вектора корреляции Z(1) , при этом отбор максимума модуля координаты проводится с учетом (запоминанием) знака этой координаты. Второй парциальный декодер, подобный схеме рис. 4.13, декодирует Y по кодовым словам 2, 31 путем вычисления n -мерного ( n 15 ) вектора корреляции Z(2) {zi(2) }, i 0, 14 , при этом отбор модуля максимальной координаты zi(2) проводится также с запоминанием знака этой
max
координаты. Окончательное решение о максимально правдоподобном переданном кодовом слове принимается в решающем устройстве РУ3 в момент времени j n 1 , где также учитывается знак максимально правдоподобной координаты. В этот же момент времени ( j n 1 ) происходит обнуление ячеек памяти АУ парциальных декодеров и СКДдекодер готов декодировать очередное кодовое слово Y .
Аппаратурная сложность АУ СКД-декодера (15,5) кода БЧХ определяется следующими значениями удельных коэффициентов сложности:
A 0,5 , |
M 0,5 . |
(4.80) |
Поскольку не все коды БЧХ обладают свойством обратных кодовых слов [3], то естественно принять, что оценка (4.80) является практически оптимальной (предельно достижимой) для предложенного рекуррентного алгоритма скользящего корреляционного декодирования двоичных циклических кодов.
В заключение отметим, что рассмотренный рекуррентный алгоритм скользящего корреляционного декодирования работает также для произвольных q ичных циклических кодов.
4.12.Быстрые ортогональные преобразования на основе совершенных двоичных решеток
В данном подразделе предложено правило построения нового клас-
са быстрых ортогональных преобразований — матриц C порядков n (2k )2 и n (3 2k )2 , k 1,2, , построенных на основе совершен-
ных двоичных решеток порядков N 2k либо N 3 2k . Показано, что бинарные ортогональные матрицы C обладают практически привлекательным свойством многопетлевого циклического сдвига ( N -сдвига), что обеспечивает эффективную процедуру скользящего метода расчета коэффициентов преобразования.

4.12. Быстрые ортогональные преобразования 161
В теории и практике ортогональных преобразований используют в основном две группы ортогональных функций: синусоидальные и прямоугольные (квадратные) [48]. Дискретизация конечного множества прямоугольных функций Хаара и Уолша на множестве равноудаленных точек приводит к образованию матриц Хаара и Адамара соответственно. Строки этих матриц служат базисными векторами при определении преобразований Хаара и Уолша-Адамара, а структурные свойства самих матриц обеспечивают построение алгоритмов
быстрых преобразований соответственно БПХ и БПУА [48]. |
|
|||||||||||
|
Представим конструктивное правило построения ортогональных |
|||||||||||
матриц преобразования C порядка n N 2 |
на основе СДР в виде про- |
|||||||||||
цедуры из двух шагов |
|
|
|
|
|
|
|
|
|
|||
|
Шаг 1. Построить порождающую (первую) строку C0 |
матри- |
||||||||||
цы C путем конкатенации последовательных строк СДР |
H(N ) |
|||||||||||
(4.19). Будем рассматривать строку C |
0 |
|
h |
h |
h |
h |
, |
|||||
, |
, |
|
|
|
0,0 , |
0,1, , |
, , |
|
N 1,N 1 |
|||
h |
1 |
1 |
как одномерный массив чисел, состоящий из N бло- |
|||||||||
ков по N чисел в каждом блоке. |
|
|
|
|
|
|
|
|
|
|||
|
Шаг 2. Построить все остальные строки Cm , m |
1, n 1 |
|
матри- |
||||||||
цы C по правилу: каждый элемент строки Cm выразить через соот-
ветствующий по номеру элемент порождающей строки C0 |
согласно |
||||||
соотношению — |
|
|
|
|
|
|
|
h(m) h(0) |
|
|
, m |
|
, |
(4.81) |
|
|
|
1, n 1 |
|||||
, |
|
|
|
|
|
||
m , m |
|
|
|
|
|||
|
|
|
|
|
|||
где индексы в правой части (4.81) редуцируются по модулю N для получения целой части Int x / N и остатка Res x / N от деления x на модуль N , т. е. определяются соотношениями:
m |
Int ( m) / N , |
(4.82) |
||
|
|
|
|
|
m Res ( m) / N . |
(4.83) |
|||
Из анализа соотношений (4.81), (4.82), (4.83) и учитывая определение СДР — соотношения (4.19) и (4.20), устанавливаем свойства матрицы преобразования C .
Свойство 4.11.1. Матрица преобразования C является ортого-
нальной симметрической матрицей |
|
CCT CC 1 nI , |
(4.84) |

162 Глава 4 | Системы бинарных фазоманипулированных сигналов. БФМ-сигналы
где CT и C 1 — ,соответственно, транспонированная и обратная матрицы порядка n каждая.
Свойство 4.11.2. Матрица C порядка n N 2 обладает свойством многопетлевого циклического сдвига — N -сдвига [34], где N — порядок СДР. Конструктивно это означает, что каждая строка Cm матрицы C получается из C0 , либо путем циклического сдвига чисел внутри каждого N -блока, либо путем циклического сдвига самих N -блоков, в зависимости от величины номера строки m 1, n 1 , как это следует из соотношений (4.82) и (4.83).
Свойство 4.11.3. Матрица C всегда может быть представлена в виде блочной структуры из n N 2 блоков размера N N каждый. Блок представляет собой подматрицу-циркулянт, при этом, в общем случае, число различных между собой структур подматриц-циркулянт равно N .
Свойство 4.11.4. Кронекеровское произведение ортогональных матриц C и известных ортогональных матриц H , ( K C H ) позволяет существенно расширить ассортимент длин n и число различных между собой структур ортогональных матриц K .
Представим в качестве примера обобщенную блочную структуру ортогональной матрицы C порядка n 16 на основе произвольной СДР порядка N 4 , как это показано в виде алгебраической конструкции (4.85).
Заметим, что циклических ортогональных матриц над алфавитом 1 не существует, за исключением единственного вырожденного случая n 4 , когда порождающая матрицу-циркулянт строка в знаковой форме (при соответствии 1 , a 1 ) имеет вид C0 . Однако на основе СДР удается построить ортогональные матрицы преобразования C со свойством многопетлевого циклического сдвига. Ни одно из ранее известных ортогональных преобразований над алфавитом 1 этим свойством не обладает.
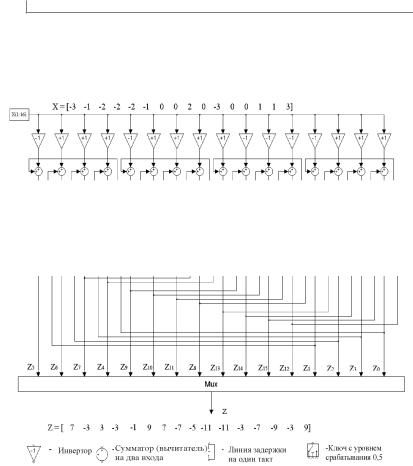
Учитывая регулярные структурные свойства матрицы преобразования C , удается разработать экономичную схему вычислителя коэффициентов преобразования. В качестве примера на рис. 4.15 представлена действующая модель экономичного вычислителя коэффициентов преобразования C , построенная в рамках математической системы MATLAB Simulink [78—80] для случая, когда СДР (в знаковой форме) имеет вид (4.86), при этом матрица ортогонального преобразования C имеет вид блочной структуры (4.87). Поскольку каждый из n блоков матрицы C представляет собой матрицу-циркулянт размера

4.12. Быстрые ортогональные преобразования 163
N N и при этом число различных по структуре блоков не более N , то для быстрого расчета коэффициентов преобразования целесообразно использовать N схем скользящего корреляционного декодирования циклических кодов (4.77) в качестве парциальных вычислителей.
C0C1C2
C3
C4
C5
C6 C C7C8C9
C10
C11
C12
C
C13
C1415
|
h |
|
h |
|
h |
|
h |
|
h |
|
h |
h |
|
h |
|
h |
|
h |
|
h |
|
h |
|
h |
|
h |
|
h |
|
h |
|
|
|
|||||
|
0,0 |
0,1 |
0,2 |
0,3 |
|
1,0 |
|
|
1,1 |
|
1,2 |
|
1,3 |
|
2,0 |
|
2,1 |
|
2,2 |
|
2,3 |
|
3,0 |
|
3,1 |
|
3,2 |
|
3,3 |
|
|
|||||||
|
h0,1 |
h0,2 |
h0,3 |
h0,0 |
h1,1 |
h1,2 |
h1,3 |
h1,0 |
h2,1 |
h2,2 |
h2,3 |
h2,0 |
h3,1 |
h3,2 |
h3,3 |
h3,0 |
|
|
||||||||||||||||||||
|
h0,2 |
h0,3 |
h0,0 |
h0,1 |
h1,2 |
h1,3 |
h1,0 |
h1,1 |
h2,2 |
h2,3 |
h2,0 |
h2,1 |
h3,2 |
h3,3 |
h3,0 |
h3,1 |
|
|
||||||||||||||||||||
|
h0,3 |
h0,0 |
h0,1 |
h0,2 |
h1,3 |
h1,0 |
h1,1 |
h1,2 |
h2,3 |
h2,0 |
h2,1 |
h2,2 |
h3,3 |
h3,0 |
h3,1 |
h3,2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
h1,0 |
h1,1 |
h1,2 |
h1,3 |
h2,0 |
h2,1 |
h2,2 |
h2,3 |
h3,0 |
h3,1 |
h3,2 |
h3,3 |
h0,0 |
h0,1 |
h0,2 |
h0,3 |
|
.(4.85) |
||||||||||||||||||||
|
h1,1 |
h1,2 |
h1,3 |
h1,0 |
h2,1 |
h2,2 |
h2,3 |
h2,0 |
h3,1 |
h3,2 |
h3,3 |
h3,0 |
h0,1 |
h0,2 |
h0,3 |
h0,0 |
|
|
||||||||||||||||||||
|
h |
|
h |
|
h |
h |
|
h |
|
|
h |
|
|
h |
|
|
h |
|
|
h |
|
h |
|
h |
|
h |
|
h |
h |
|
h |
h |
|
|
||||
|
1,2 |
1,3 |
|
1,0 |
1,1 |
|
2,2 |
|
2,3 |
|
2,0 |
|
2,1 |
|
3,2 |
|
3,3 |
|
3,0 |
|
3,1 |
0,2 |
0,3 |
|
0,0 |
|
0,1 |
|
|
|||||||||
|
h1,3 |
h1,0 |
h1,1 |
h1,2 |
h2,3 |
h2,0 |
h2,1 |
h2,2 |
h3,3 |
h3,0 |
h3,1 |
h3,2 |
h0,3 |
h0,0 |
h0,1 |
h0,2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h2,0 |
h2,1 |
h2,2 |
h2,3 |
h3,0 |
h3,1 |
h3,2 |
h3,3 |
h0,0 |
h0,1 |
h0,2 |
h0,3 |
|
h1,0 |
|
h1,1 |
|
h1,2 |
h1,3 |
|
|
|||||||||||||||||
|
h |
2,1 |
h |
2,2 |
h |
2,3 |
h |
2,0 |
h |
3,1 |
h |
3,2 |
h |
3,3 |
h |
3,0 |
h |
h |
h |
h |
|
h |
h |
|
h |
h |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
0,2 |
|
0,3 |
|
0,0 |
|
1,1 |
|
1,2 |
|
1,3 |
|
1,0 |
|
|
||||||||
|
h2,2 |
h2,3 |
h2,0 |
h2,1 |
h3,2 |
h3,3 |
h3,0 |
h3,1 |
h0,2 |
h0,3 |
h0,0 |
h0,1 |
h1,2 |
h1,3 |
|
h1,0 |
h1,1 |
|
|
|||||||||||||||||||
|
h2,3 |
h2,0 |
h2,1 |
h2,2 |
h3,3 |
h3,0 |
h3,1 |
h3,2 |
h0,3 |
h0,0 |
h0,1 |
h0,2 |
h1,3 |
h1,0 |
|
h1,1 |
h1,2 |
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h3,0 |
h3,1 |
h3,2 |
h3,3 |
h0,0 |
h0,1 |
h0,2 |
h0,3 |
|
h1,0 |
|
h1,1 |
|
h1,2 |
h1,3 |
h2,0 |
h2,1 |
h2,2 |
h2,3 |
|
||||||||||||||||||
|
h3,1 |
h3,2 |
h3,3 |
h3,0 |
h0,1 |
h0,2 |
h0,3 |
h0,0 |
|
h1,1 |
|
h1,2 |
|
h1,3 |
h1,0 |
h2,1 |
h2,2 |
h2,3 |
h2,0 |
|
|
|||||||||||||||||
|
h3,2 |
h3,3 |
h3,0 |
h3,1 |
h0,2 |
h0,3 |
h0,0 |
h0,1 |
h1,2 |
|
h1,3 |
|
h1,0 |
h1,1 |
h2,2 |
h2,3 |
h2,0 |
h2,1 |
|
|||||||||||||||||||
|
h3,3 |
h3,0 |
h3,1 |
h3,2 |
h0,3 |
h0,0 |
h0,1 |
h0,2 |
h1,3 |
|
h1,0 |
|
h1,1 |
h1,2 |
h2,3 |
h2,0 |
h2,1 |
h2,2 |
|
|||||||||||||||||||
|
|
|
|
|
|
H(4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.
(4.86)
(4.87)
Результаты промежуточных расчетов парциальных вычислителей используются многократно с помощью несложной схемы
164 Глава 4 | Системы бинарных фазоманипулированных сигналов. БФМ-сигналы
синхронизации, как это видно из потактового рассмотрения работы вычислителя рис. 4.15 и анализа структуры синхропоследовательности S 0111011101110111 .
Рис. 4.15. Модель экономичного вычислителя коэффициентов преобразования C (4.87)
Синхропоследовательность S управляет синхронной работой всех ключей, имеющих одинаковый уровень порога переключения, равный 0,5. Для реализации схемы быстрого вычисления коэффициентов преобразования C требуется, в общем случае, n сумматоров (вычитателей) и n ячеек памяти, каждая на один такт работы. Обозначим сокращенно вычислитель быстрого преобразования C как ВБПС.
Заметим, что для реализации схемы быстрого вычисления коэффициентов преобразования Уолша-Адамара — ВБПУА также с максимальным
