Sistemy_shirokopolosnoy_radiosvyazi_2009

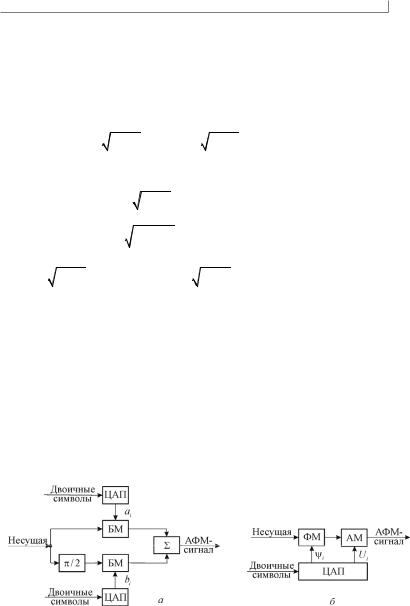
250 Глава 7 | Сигнально-кодовые конструкции. (Треллис-модуляция)

При формировании АФМ-сигналов в декартовой системе координат (рис. 7.1, а) передаваемые двоичные символы поступают на цифроаналоговые преобразователи (ЦАП) блоками длиной k log2 m . Вырабатываемые ЦАП сигналы ai и bi модулируют квадратурные составляющие несущего колебания в балансных модуляторах (БМ). В схеме формирования АФМ-сигналов, заданных в полярной системе координат (рис. 7.1, б), ЦАП вырабатывает из двоичных блоков величины i и Ui для модуляции несущей последовательно в фазовом (ФМ) и в амплитудном (АМ) модуляторах.

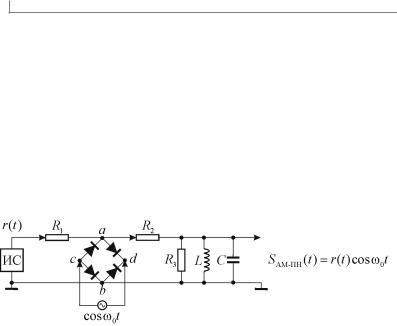
Схема балансного модулятора (БМ), например, кольцевого с диодным ключом, представлена на рис 7.2.

Рис. 7.2. Балансный (кольцевой) модулятор с диодным ключом для получения амплитудно — модулированных сигналов с подавленной несущей — АМ-ПН

Каждый кольцевой балансный модулятор на схеме рис 7.1, а формирует АМ-сигнал с подавленным несущим колебанием (АМ-ПН). Вся эта схема с фазосдвигающей цепочкой на / 2 формирует сигнал однополосной амплитудной модуляции (одна боковая полоса) с подавленной несущей (ОБП-ПН), который в общем случае можно представить выражением

SОБП ПН (t) r(t)cos( 0t 0 ) rˆ(t)sin( 0t 0 ) ,

где знак плюс соответствует однополосному сигналу с нижней боковой полосой, а знак минус — с верхней, функция rˆ(t) является преобразованием Гильберта сообщения r(t) .

В общем случае задача синтеза оптимального ансамбля АФМ-сигналов сводится к задаче плотнейшей укладки сфер (или окружностей) [8] в заданном объеме n -мерного пространства — рис. 7.3.

7.3. Правила и схемы формирования КАМ-сигналов 251

Рис. 7.3. Ансамбли АФМ-сигналов: а — расположение сигнальных точек в вершинах правильных треугольников (треугольных сетей); б — расположение сигнальных точек в вершинах квадратных сетей; в — круговые расположения сигнальных точек

При синтезе АФМ-сигналов нужно так расположить сигнальные точки, чтобы собственные области каждого сигнала были одинаковы по объему или по площади. Собственная область сигнала — это область правильного приема сигнала. Для дискретных сообщений вероятность правильного приема есть вероятность попадания конца вектора принятого сигнала y(t) Si (t) n(t) в собственную область Gi . Большинство ансамблей АФМ-сигналов найдены эвристическим методом: на основе треугольной сети, квадратной сети и концентрических круговых расположений (рис. 7.3).

7.3. Правила и схемы формирования КАМ-сигналов

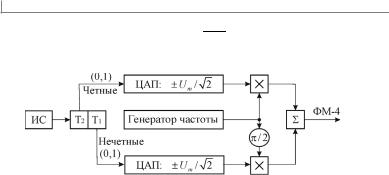
Манипуляционные коды Грея. Поскольку соотношение (7.5) есть квадратурное представление сигнала, то другое название амплитуднофазовой модуляции — квадратурная амплитудная модуляция (КАМмодуляция), при этом АФМ-сигналы называют часто КАМ-сигналами. Простейшая базовая схема квадратурного модулятора — это схема формирования сигналов ФМ-4 — рис. 7.4.

Из анализа алгоритма работы схемы модулятора ФМ-4 следует, что двоичный цифровой поток данных (ЦПД) от источника сообщений

(ИС) разбивается в модуляторе на пакеты i { i,1, i,2 }, i {0,1} размера k 2 (две триггерные ячейки памяти T1 и T2 ). Каждому па-

кету ставится в однозначное соответствие ( ) свой сигнал по схеме

252 Глава 7 | Сигнально-кодовые конструкции. (Треллис-модуляция)

Рис. 7.4. Схема квадратурного модулятора сигналов ФМ-4

Ясно, что общее число правил кодирования 2k ! 22! 24 . Окончательный выбор вида манипуляционного кода (7.8) осуществляется из следующих соображений. Наиболее часто ошибки в различении сигналов происходят за счет переходов в области соседних сигналов (сигналы с минимальным расстоянием Евклида dE ), следовательно, двоичные последовательности (пакеты) сообщений, приписываемые соседним сигналам, должны отличаться наименьшим числом двоичных символов, т. е. иметь минимальное расстояние Хэмминга dX . Этому условию практически отвечает манипуляционный код на основе кода Грея. Коды Грея (или рефлексные коды) широко используются в задачах аналого-дискретных преобразований и обладают тем свойством, что каждые два соседние кодовые слова отличаются лишь на одну единицу, т. е. расстояние Хэмминга между

ними dX 1 .

Строятся коды Грея таким образом. Пусть натуральное десятичное число N представлено истинным двоичным кодовым словом A , т. е. (N )10 (A)2 . Тогда соответствующее кодовое слово кода Грея определяется по следующему конструктивному правилу:

где символ означает операцию поэлементного суммирования по модулю 2, а выражение A 1 означает нециклический сдвиг вправо на один элемент двоичного слова A с последующим удалением младшего разряда и восстановлением нулевого значения старшего разряда (слева).

Пример. Пусть десятичное число (12)10 (1100)2 , тогда соответствующее кодовое слово кода Грея

7.3. Правила и схемы формирования КАМ-сигналов 253

Сигнальное созвездие. Пользуясь геометрической трактовкой, каждый КАМ-сигнал можно изобразить вектором в n -мерном сигнальном пространстве. Отмечая только концы векторов, получаем изображение сигнала в виде сигнальной точки (рис. 7.3), координаты которой определяются значениями пары (ai ,bi ) . Совокупность сигнальных точек образует так называемое сигнальное созвездие (signal constellation). На рис. 7.5 показан пример сигнального созвездия ФМ-4.

Рис. 7.5. Сигнальное созвездие ФМ-4 на основе кода Грея длины n 2

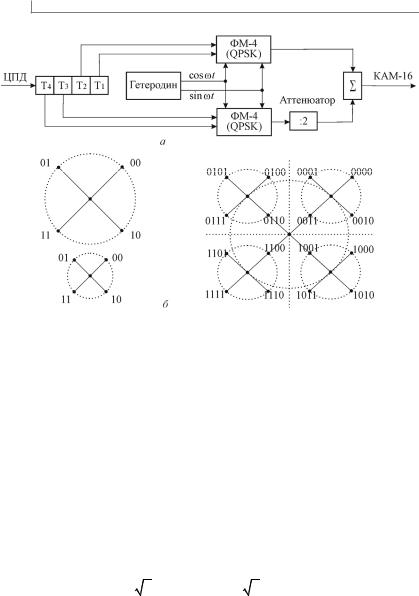
Для построения ансамблей сигналов КАМ-16, КАМ-32, , КАМ-512 на практике часто используют метод наложенной модуляции, или по-другому, метод суперпозиции. Например, используя два одинаковых модулятора ФМ-4 (рис. 7.4), построим схему модулятора КАМ-16 — рис. 7.6.

254 Глава 7 | Сигнально-кодовые конструкции. (Треллис-модуляция)

Рис. 7.6. Схема модулятора КАМ-16 — а и сигнальное созвездие КАМ-16 — б

7.4. Помехоустойчивость сигналов КАМ и ФМ

На основании спектральной теории сигналов нетрудно установить, что при равном числе точек m в сигнальном созвездии спектр сигналов КАМ- m идентичен спектру сигналов ФМ- m . Однако помехоустойчивость систем КАМ и ФМ различна. Из теории потенциальной помехоустойчивости В. А. Котельникова следует, что предельная помехоустойчивость системы радиосвязи зависит от минимального расстояния Евклида dE между соседними сигналами при прочих равных условиях. Проведя геометрическое рассмотрение и анализ сигнального созвездия КАМ- m при условии, что m 2L , L — число уровней модуляции, находим

аналогично для ФМ

7.5. Алгоритм работы и схема универсального демодулятора ФМ-сигналов 255

где m — число фаз.

При большом числе m сигналов в ансамбле вероятность ошибки в основном зависит от минимального расстояния dE между ближайшими сигнальными точками. Поэтому сравнение ансамблей удобно

где EС — энергия m -ичного сигнала.

Из анализа выражений (7.10) и (7.11) следует, что системы КАМ предпочтительнее систем ФМ. Например, при значении

чивают выигрыш в средней энергии по сравнению с системами ФМсигналов. Например, для фиксированного значения вероятности ошибки pош 10 5 и m 32 значение выигрыша составляет 7,1 дБ.

Очевидно, что применение АФМ-сигналов требует высокой линейности и стабильности параметров приемопередающего тракта, а также линейности и достаточного амплитудного диапазона всего канала связи. В то же время ФМ-сигналы допускают исключительно простую техническую реализацию демодулятора оптимального различения этих сигналов, как это показано в следующем подразделе.

7.5.Алгоритм работы и схема универсального демодулятора ФМ-сигналов

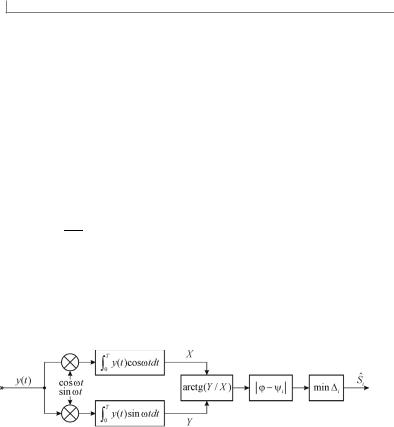
Реализация оптимального приема АФМ-сигналов плотнейшей укладки во многих случаях представляет значительные трудности. Поэтому поиск подходящих ансамблей часто обусловлен соображениями простоты устройств формирования и обработки сигналов на приеме. Рассмотрим алгоритм построения экономичных схем демодуляторов ФМ-сигналов. Из анализа соотношения (7.7) следует, что каждый ФМ-сигнал полностью определяется своей фазой i 2 i / m , т. е. является однопараметрическим сигналом. Следовательно, задача различения сигналов может быть сведена к задаче максимально правдоподобного оценивания одного параметра принятого в условиях

7.6. Сигнально-кодовые конструкции (треллис-модуляция) 257

высокоскоростных протоколах сигналы КАМ используются совместно с помехоустойчивыми сверточными кодами. Сочетание методов многопозиционной модуляции и помехоустойчивого кодирования дает возможность повысить либо энергетическую эффективность без уменьшения частотной, либо частотную эффективность без снижения энергетической, а в ряде случаев оба параметра.

Задача заключается в формировании сигнальных последовательностей, которые можно достаточно плотно разместить в многомерном пространстве (для повышения частотной -эффективности) и в то же время разнести на достаточно большие расстояния (для обеспечения высокой энергетической -эффективности). Такие последовательности, построенные на базе помехоустойчивых кодов и многопозиционных сигналов с плотной упаковкой, называются сигнальнокодовыми конструкциями — СКК, или треллис-модуляцией (Trellis Coded Modulation). Характер обмена между и эффективностью для СКК в зависимости от роста их объема m поясняется с помощью табл. 7.3.

Таблица 7.3

Сигнально-кодовые конструкции

Заметим, что задача поиска наилучшей СКК является одной из наиболее сложных задач общей теории связи. Современные высокоскоростные протоколы модуляции (V. 32, V. 32bis, V. 34 и др.) предполагают обязательное применение сигнально-кодовых конструкций. Все применяемые сегодня СКК используют высокоскоростные свер-

точные коды вида (k0 /n0 ) (n0 1/n0 ) .

Типичный сверточный код, применяемый совместно с модулятором ФМ-8, имеет относительную скорость k0 / n0 2 / 3 (рис. 7.8).

258 Глава 7 | Сигнально-кодовые конструкции. (Треллис-модуляция)

Рис. 7.8. Схема кодера сверточного (2/3) -кода

Каждый сверточный код (СК) можно задать с помощью: схемы; уравнений кодирования; импульсной характеристики; диаграммы состояний и решетчатой диаграммы [2,4]. Основной вопрос, на который нужно ответить при построении СК, это какова его корректирующая способность.

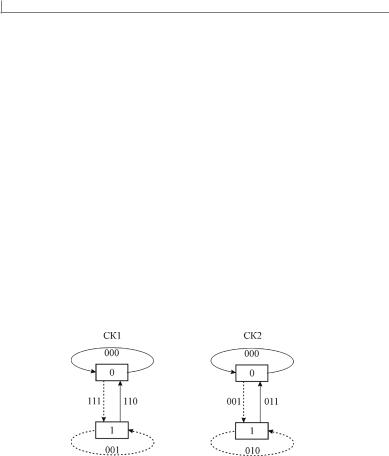
Изложим простой метод нахождения корректирующей способности СК. Корректирующая способность СК определяется его свободным расстоянием dСВ 2t 1 , т. е. минимальным суммарным весом двух или более ребер решетчатой диаграммы при нетривиальном переходе кодера из состояния «0» в состояние «0». Для решения этой задачи будем считать, что кодер (рис. 7.8) состоит из двух параллельно соединенных парциальных кодеров соответственно по первому входу и по второму входу. Импульсная характеристика первого парциального сверточного кода (СК1): h1(n) 111110 , а второго — h2 (n) 001011 . На рис. 7.9 построены диаграммы состояний [2,4] парциальных кодов СК1 и СК2.

Рис. 7.9. Диаграммы состояний парциальных кодов СК1 и СК2, построенных на основе сверточного кода рис. 7.8

Поскольку рассматриваемый СК (рис. 7.8) может принимать всего 4 состояния, и при этом за один такт работы возможен переход в любое из состояний, то для нахождения минимального свободного расстояния достаточно рассмотреть сумму весов различных пар ребер (выходных кадров) решетчатой диаграммы (при осуществлении нетривиальных переходов кодера из состояния «0» в состояние «0»), как это показано на схеме рис. 7.10.