Глава 9 физические основы квантовых приборов

9.1. Энергетические уровни

Как известно, энергия свободной частицы может принимать лю­бые значения. Квантовая система, состоящая из микрочастиц, электронов, ядер, атомов и т. д., отличается тем, что ее внутрен­няя энергия, т. е. энергия, не связанная с движением системы как целого, может принимать только дискретные значения. Воз­можные дискретные значения энергии называют энергетическими уровнями.

В свободных атомах квантуется энергия электронов и имеется система энергетических уровней электронов, или система элек­тронных уровней атома. Наблюдаются сле­дующие движения частиц: движение элек­тронов в атоме, колебания атомов в моле­куле, вращение и поступательное движение молекул. Энергия трех видов движения, кроме поступательного, квантуется. 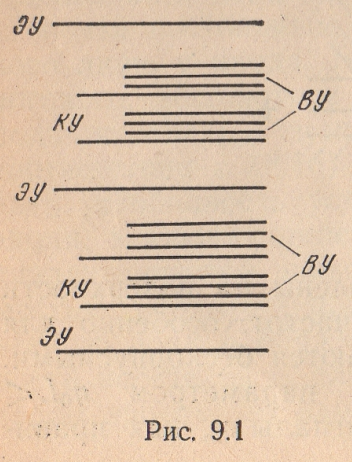Кван­тование энергии приводит к образованию сложной системы энергетических уровней, показанной на рис. 9.1. Основой системы являются электронные уровни ЭУ, отстоя­щие друг от друга на . Между электронными уровнями располагаются ко­лебательные уровни КУ с расстоянием примерно , а между колебательными уровнями находятся вращательные уровниВУ с интервалом и менее. Переходы между электронными уровнями соот­ветствуют излучению в видимом и ультрафиолетовом диапазонах, между колебательными уровнями — инфракрасному, а между вра­щательными — СВЧ диапазону.

В твердых телах взаимодействие частиц становится настолько сильным, что образуются зоны с очень близко расположенными уровнями, между этими зонами имеются зоны запрещенных зна­чений энергии (запрещенные зоны).

В атомах осуществляются только те переходы между энерге­тическими уровнями, которые удовлетворяют правилам отбора, устанавливающим допустимые различия квантовых чисел. Пере­ходы, удовлетворяющие правилам отбора, называются разрешен­ными, а остальные — запрещенными.

Переходы с излучением или поглощением квантов электро­магнитной энергии (фотонов) называют излучательными, а пере­ходы, в которых квант энергии выделяется в виде тепла в сре­де — безизлучательными. Состояние, из которого запрещены все излучательные переходы в более низкие энергетические состояния, называется метастабильным. Эти состояния играют важную роль в квантовых приборах.

9.2. Квантовые переходы

Спонтанные переходы — самопроизвольные квантовые перехо­ды частицы из верхнего энергетического состояния в нижнее. Уровень, соответствующий наименьшей возможной энергии, на­зывается основным, а остальные — возбужденными. Спонтанные переходы могут сопровождаться электромагнитным излучением (испускание квантов энергии). Частота излучения определяется из постулата Бора

(9.1)

где , — энергия верхнего (j) и нижнего (i) уровней; h — постоянная Планка. Частота

(9.2)

называется частотой квантового перехода.

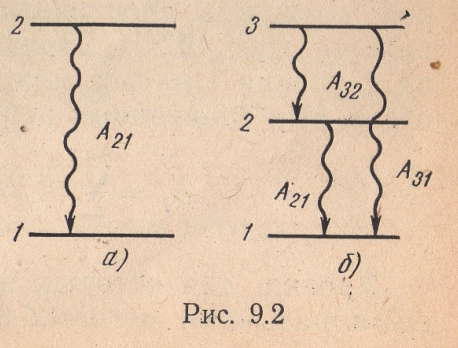
Число частиц с одинаковой энерги­ей в единице объема называется населенностью уровня. Пусть номер верхнего уровня , а нижнего (рис. 9.2а). Обозначим населенности этих уровней и . При спонтан­ных переходах происходят изменение населенности уровней, уменьшение верхнего и увеличение нижне­го .

Уменьшение населенности уровня в результате только спон­танных переходов за время dt пропорционально населенности этого уровня и времени dt:

, (9.3)

где — коэффициент Эйнштейна для спонтанных переходов, определяющий вероятность спонтанного перехода в с.

Решив (9.3), получим экспоненциальный закон уменьшения населенности уровня 2 во времени:

(9.4)

где — населенность в момент времени .

Насколько уменьшится населенность , настолько же возрас­тет населенность , так как общее число частиц в объеме оста­ется неизменным. Из (9.4) следует, что через время на­селенность уменьшится в раза по сравнению с на­чальным значением . Величина

(9.5)

характеризует время жизни частицы в возбужденном состоянии и называется временем жизни на уровне. Коэффициент Эйнштей­на определяет среднее число спонтанных переходов в еди­нице объема в с, или среднее число частиц, совершивших са­мопроизвольный переход из верхнего состояния в нижнее, т. е. имеет размерность и может быть любым, в отличие от матема-­ тической вероятности, меняющейся отдо.

За с в единице объема число спонтанных переходов

(9.6)

При каждом спонтанном переходе частицы выделяется квант энергии (9.1), поэтому за с с учетом (9.6) излучается энергия

(9.7)

Случайность спонтанных переходов означает, что различные частицы излучают не одновременно и независимо, т. е. фазы элек­тромагнитных волн, излучаемых отдельными частицами, не сог­ласованы друг с другом. Поэтому спонтанное излучение отдель­ных частиц не когерентно между собой. Излучение обычных ис­точников света есть результат спонтанных переходов.

В системе частиц, имеющих несколько энергетических уров­ней, возможны спонтанные переходы частиц с данного уровня на нижние (рис. 9.26). Полная вероятность спонтанного перехо­да с уровня на все нижние уровни равна сумме вероятностей отдельных спонтанных переходов :

(9.8)

Уровни, для которых вероятность спонтанных переходов очень мала, называют метастабильными.

Время жизни на уровне в многоуровневой системе опреде­ляется аналогично (9.5) с учетом (9.8):

(9.9)

Вынужденные переходы — это квантовые переходы частиц под действием внешнего электромагнитного поля, частота которого совпадает или близка к частоте перехода. При этом возможны переходы с верхнего уровня на нижний и с нижнего на верх­ний. В первом случае под действием внешнего электромагнитного поля с частотой происходит вынужденное испускание кванта энергии . Особенность вынужденного испускания состоит в том, что появившийся фотон полностью идентичен фотону внеш­него поля. Вынужденное излучение имеет такие же частоту, фа­зу, направление распространения и поляризацию, как и вынуж­дающее излучение. Поэтому вынужденное излучение увеличивает энергию электромагнитного поля с частотой перехода . Это служит предпосылкой для создания квантовых усилителей и гене­раторов.

Следует отметить, что на вынужденный переход с излучением энергии не затрачивается энергия внешнего поля, которое явля­ется лишь своеобразным стимулятором процесса. В противопо­ложность этому для перевода частицы из нижнего энергетическо­го состояния в верхнее необходимо затратить энергию внеш­него поля, равную разности энергии верхнего и нижнего уровней: . Таким образом, при каждом вынужденном переходе снизу вверх затрачивается квант энергии внешнего поля .

Вынужденные переходы, так же как и спонтанные, имеют ста­тистический характер. Поэтому вводятся вероятностные коэффи­циенты: — вероятность вынужденного перехода сверху вниз и — снизу вверх в с. Эти вероятности пропорциональны объемной плотности энергии внешнего поля в единичном спек­тральном интервале на частоте перехода и определяются соотно­шениями

, (9.10)

где и — коэффициенты Эйнштейна для вынужденных пе­реходов с излучением и поглощением энергии соответственно.

Коэффициенты и имеют смысл вероятностей вынуж­денных переходов в с при единичной объемной плотности энер­гии внешнего поля .

Число вынужденных переходов сверху вниз с излучением энер­гии в единицу времени в единице объема пропорционально ве­роятности и населенности верхнего уровня , т. е. с учетом (9.10)

. (9.11)

Аналогично при тех же условиях число вынужденных перехо­дов снизу вверх с поглощением энергии

. (9.12)

Соотношения между коэффициентами Эйнштейна. Связь меж­ду коэффициентами Эйнштейна , и можно установить, предполагая, что внутри полости, представляющей абсолютно черное тело, находится система атомов при температуре .

Пусть система атомов имеет два уровня энергии и , при переходах между которыми излучается или поглощается квант энергии . При термодинамическом равновесии в системе не происходит изменения энергии, поэтому число излученных кван­тов должно быть равно числу поглощенных. Следовательно, в еди­ницу времени во всей системе общее число переходов из верхне­го энергетического состояния в нижнее должно быть равно обще­му числу переходов из нижнего состояния в верхнее:

(9.13)

В состоянии равновесия в системе имеется равновесная плот­ность поля излучения , которая определяет число вынужден­ных переходов в системе.

Полное число переходов сверху вниз в (9.13) в состоянии равновесия определяется суммой числа спонтанных переходов и вынужденных переходов с излучением энергии , т. е. с учетом (9.6) и (9.11)

. (9.14)

Число переходов снизу вверх определяется только вынужден­ными переходами с поглощением, т. е. с учетом (9.12)

. (9.15)

Приравнивая на основании (9.13) и , получаем

. (9.16)

Из (9.16) найдем равновесную плотность энергии поля

(9.17)

Соотношение населенностей уровней в состоянии термодинамиче­ского равновесия определяется законом Больцмана

,

где и — статистический вес уровней; — постоянная Больц­мана; — абсолютная температура.

Для невырожденных уровней закон Больцмана принимает более простую форму записи

. (9-18)

которая и будет далее использоваться. Подставляя (9.18) в (9.17) и учитывая, что получаем

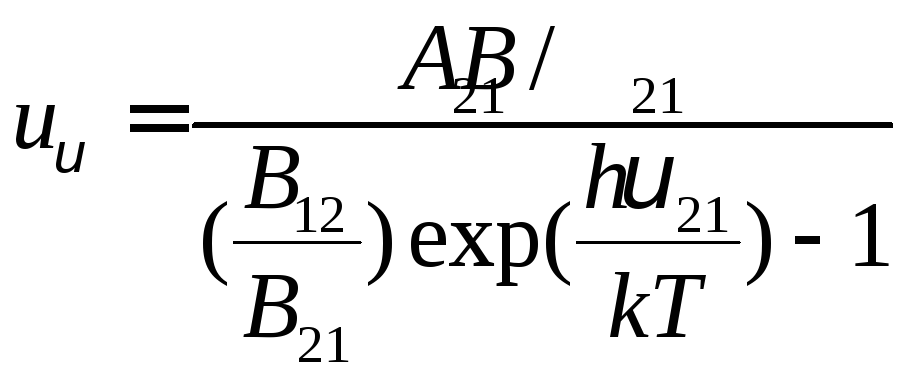(9.19)

Эйнштейн постулировал, что равновесная спектральная плот­ность энергии поля должна быть равна ее значению, рассчитан­ному по формуле Планка для равновесного излучения абсолютно черного тела:

если вместо подставить .

Сравнивая с учетом этого (9.20) с (9.19), получаем условия тождественности этих формул:

, (9.21)

. (9.22)

Таким образом, если квантовая система и поле излучения на­ходятся в состоянии термодинамического равновесия, то вероят­ности вынужденных переходов в единицу времени при единичной плотности полей и должны быть одинаковы. Вероятность спонтанных переходов пропорциональна третьей степени частоты перехода, поэтому спонтанное излучение сильнее всего проявляет­ся в оптическом диапазоне волн.

Безызлучательные переходы. Атомы и молекулы газа в ре­зультате неупругих соударений друг с другом или с электронами теряют или приобретают энергию. При этом энергия электромаг­нитного поля не излучается, не поглощается. Такие энергетичес­кие переходы принято называть безызлучательными. В твердом теле безызлучательные переходы происходят вследствие колеба­тельного движения кристаллической решетки.

Безызлучательные переходы характеризуются также вероят­ностью перехода между уровнями и сверху вниз и снизу вверх соответственно с потерей и получением порции энергии .

В соответствии с принципом детального равновесия в состоя­нии термодинамического равновесия подобно (9.13) число безызлучательных переходов с уровня на уровень в с равно числу обратных безызлучательных переходов с уровня на уровень :

В состоянии термодинамического равновесия распределение

населенностей определяется законом Больцмана (9.18). С уче­том (9.2) получаем

, (9.23)

Из (9.23) следует, что вероятность безызлучательных перехо­дов сверху вниз больше, чем снизу вверх, Т. е. (), в отличие от вероятностей вынужденных переходов, которые оди­наковы . Если , что обычно справедливо для квантовых приборов СВЧ диапазона, то (9.23) можно заменить приближенным выражением

(9.24)

Релаксационные переходы. Изолированная система, в которой распределение частиц по энергии отличается от равновесного, на­зывается неравновесной. Неравновесное состояние наблюдается при внешнем воздействии, после прекращения которого система возвращается в равновесное состояние. Процесс установления равновесия в системе называется релаксацией, а переходы частиц с одного уровня на другой в процессе релаксации — релаксаци­онными переходами. В основе процесса релаксации лежит взаимо­действие частиц (электронов, атомов, молекул, ионов) между собой и со стенками объема. Рассмотренные безызлучательные перехо­ды являются релаксационными. К релаксационным переходам следует отнести и спонтанные, роль которых велика в оптическом диапазоне. Релаксационные переходы приходится учитывать при рассмотрении процессов, выводящих систему из равновесного со­стояния. При постоянном внешнем воздействии возможна компен­сация релаксационных процессов, тогда система будет находиться в стационарном неравновесном состоянии. Релаксационные пере­ходы влияют также на ширину спектральной линии. Это влияние рассмотрено в § 9.3.