1.2.6. Рух тіл змінної маси

Існує багато випадків, коли маса тіла змінюється в процесі руху за рахунок неперервного відокремлення або приєднання речовини (наприклад, ракета, реактивний літак, рухома на воді баржа, яку навантажують піском, чи швидка вагонетка, в яку досипають щебінь, тощо. Виявляється, що закони руху таких тіл змінної маси можна отримати, виходячи із закону збереження імпульсу. Для цього, як приклад, розглянемо політ ракети у космос (рис. 1.24).

Нехай у початковий момент часу t ракета має масу m, її швидкість в інерціальній системі відліку, пов’язаній із далекими зорями, рівна . Таким чином, її початковий імпульс.

У момент часу маса ракети внаслідок витікання газів змінилася на величинуі стала рівна. Зауважимо, що. Імпульс ракети стане рівним. Імпульс газів буде:, причому. Тоді в момент часуімпульс системи “ракета-гази” рівний:

.

Знайдемо приріст імпульсу:

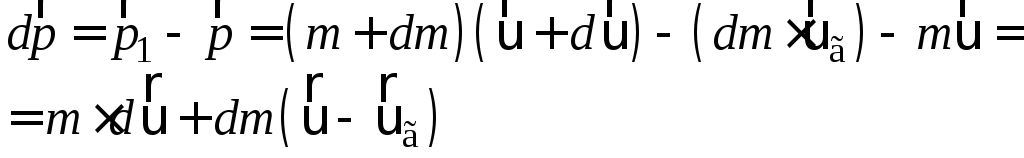(1.73)

Оскільки за другим законом Ньютона , то

(1.74)

або

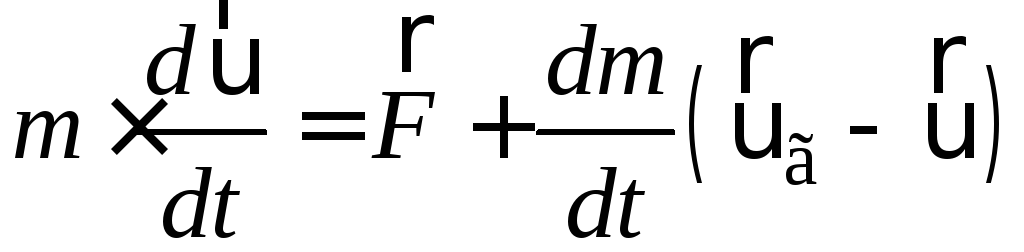(1.75)

Рівняння (1.75) називається рівнянням Мещерського і описує реактивних рух ракети. У цьому рівнянні може бути будь-якою зовнішньою силою.

Введемо позначення. Доданок 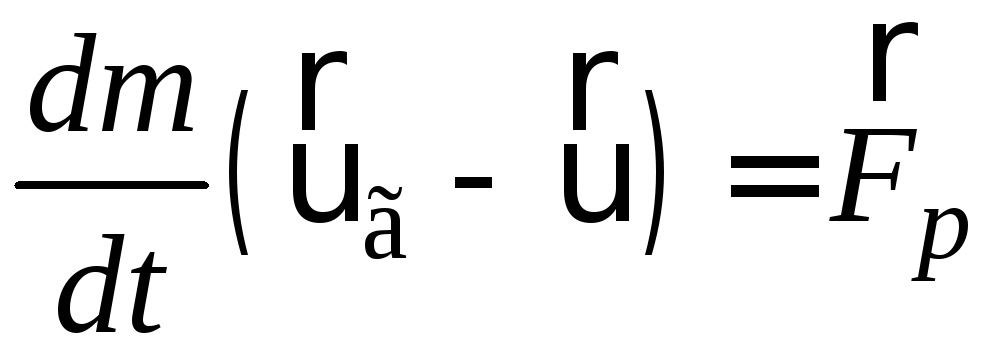– називаєтьсяреактивною силою, швидкість витікання газів відносно ракети – відносною швидкістю. Таким чином, можна зробити висновок про те, що реактивна сила тим більша, чим більша швидкість згорання паливаі чим більша відносна швидкість.

Розглянемо приклад руху ракети лише за рахунок реактивної сили тяги двигуна. У цьому випадку рівнянням її руху буде:

(1.76)

У проекції на вертикальну вісь останнє рівняння матиме вигляд:

(1.77)

Або . Після інтегрування отримаємо:

(1.78)

Константу С знайдемо із початкових умов: t = 0, υ = 0, m = m₀, де m₀ – початкова (стартова) маса ракети. Тоді C = υ_вln(m₀). Таким чином, рівняння (1.78) набуде вигляду:

(1.79)

або

(1.80)

Рівняння (1.80) називається формулою Ціолковського. Воно дозволяє обчислити таку стартову масу палива, необхідну для того, щоб ракета досягла в кінці свого польоту швидкості .

Користуючись рівнянням Ціолковського, оцінимо затрати при космічних польотах.

Політ до планет. _в = 4 км/с, кінцева швидкість ракети = 16 км/с. Тоді стартова маса ракетиm₀ ≈ 60∙m. Такі ж міркування слід застосувати при розрахунку зворотного польоту ракети у напрямку до Землі. Тоді m₀ ≈ 60∙m', де m' – кінцева маса ракети після її повернення на Землю. Таким чином, відношення стартової маси ракети на початку польоту до кінцевої маси ракети після його завершення: m₀ /m' = 3600.

Політ до зірок. Відстані до зірок вимірюються світловими роками – від найближчої зірки світло йде до Землі близько 4 років. Тому для досягнення навіть найближчих зірок потрібні космічні кораблі, швидкості яких близькі до швидкості світла c. При швидкості ракети  = 0,25∙c та швидкості витікання газів _в = 10 км/с на кожну тонну корисного вантажу має припадати 5∙10³³²⁷ тон палива! Для порівняння – маса Сонця M_C = 2∙10³⁰ кг, маса галактики M_гал ≈ 10⁵³ кг. Навряд чи є сенс говорити про рух настільки фантастично гігантського космічного корабля щодо Всесвіту, що має в порівнянні з ним мізерну масу.

Отже, для міжзоряних перельотів ракети на хімічному паливі абсолютно непридатні. Для перетворення ракети в зореліт, перш за все, необхідно підвищити швидкість витікання струменя, наблизивши її до швидкості світла. Ідеальним був би випадок _в = с. Так було б у фотонній ракеті, в якій роль газового струменя мав би грати світловий пучок. Реактивна сила в фотонній ракеті здійснювалася б тиском світла. Перетворення речовини у випромінювання постійно відбувається всередині зірок. Цей процес здійснюється і на Землі (вибухи атомних і водневих бомб). Чи можливо надати йому керований характер і будуть використані в фотонних ракети – на це питання відповідати зараз передчасно.