1.2.2. Принцип відносності Галілея

Оскільки перший закон постулює існування інерціальних систем відліку, то знайдемо зв’язок між законами руху одного і того ж тіла в різних інерціальних системах відліку. Для цього розглянемо дві системи відліку: інерціальну нерухому систему К і систему К′, що рухається відносно системи К із постійною швидкістю . Виберемо відповідні координатні осі обох систем таким чином, щоб осі х та х′ співпадали, а осі y і y′, а також z і z′ були паралельні одна одній. Нехай в момент часу t рухома точка знаходиться в положенні А. За цей же час початок координат О′ системи К′ змістився на відстань від початку координат О системи К (рис. 1.20). Тоді радіус-вектор будь якої точки А у моменти часу t  і t′ у системах К і К′ пов’язані простими співвідношеннями:

(1.51)

У проекціях на координатні осі співвідношення (1.49) матиме вигляд:

(1.52)

Формули (1.51) та (1.52) називаються перетвореннями Галілея.

Диференціюючи співвідношення (1.51) по часу отримаємо:

або

(1.53)

де – швидкість точки в системіК, а – в системіК′.

Формула (1.53) виражає класичний закон додавання швидкостей.

Диференціюючи другий раз, отримаємо:

Оскільки швидкість рухомої системи К′ відносно нерухомої К постійна: , то залишається:

(1.54)

де – прискорення точки в системіК, – прискорення тієї ж точки в системіК′. Таким чином, прискорення в обох системах відліку однакове, тобто є інваріантним відносно перетворень Галілея.

Оскільки маса, як і прискорення, теж незмінна в усіх інерціальних системах відліку, то згідно рівняння (1.54) не повинна змінюватися і результуюча сила, що діє на тіло. У цьому полягає основний постулат класичної механіки, який називається класичним галілеєвським принципом відносності: Рівняння руху класичної динаміки однакові в усіх інерціальних системах відліку, тобто усі інерціальні системи відліку еквівалентні (рівноправні) стосовно механічних явищ.

Або інакше: знаходячись всередині ізольованої інерціальної системи відліку ніякими механічними дослідами не можна встановити, рухається система рівномірно і прямолінійно чи знаходиться у стані спокою.

1.2.3. Закон динаміки системи матеріальних точок

Третій закон Ньютона в поєднанні із другим та третім законами дозволяє перейти від динаміки окремої матеріальної точки до динаміки довільної механічної системи.

Розглянемо задачу опису руху системи матеріальних точок. Матеріальні точки, що входять в матеріальну систему, можуть взаємодіяти одна з одною (внутрішні сили), а також з матеріальними точками, що не входять до складу системи (зовнішні сили). Якщо зовнішні сили відсутні чи взаємно скомпенсовані, то система матеріальних точок називається замкненою або ізольованою. Сказане справджується і для твердого тіла, оскільки його можна змоделювати системою з n матеріальних точок. Якщо тіло абсолютно тверде, його модель представляє собою незмінну систему матеріальних точок.

Розглянемо систему n матеріальних точок масою m_і кожна, що мають імпульси . В загальному випадку на довільнуi-ту матеріальну точку системи діють:

а) внутрішні сили зі сторони матеріальних точок, що входять до складу системи:

(1.55)

де – сила, що діє наi-ту матеріальну точку зі сторони k-ї, причому i ≠ k, оскільки матеріальна точка не може взаємодіяти сама з собою. Тому загальна кількість точок, що взаємодіють із вибраною i-тою точкою буде n – 1;

б) зовнішні сили, прикладені до i-ї матеріальної точки зі сторони тіл, що не входять до складу системи. Позначимо символом рівнодійну усіх зовнішніх сил, що діють наi-ту матеріальну точку. Тоді рівняння руху кожної матеріальної точки можна записати у наступному вигляді:

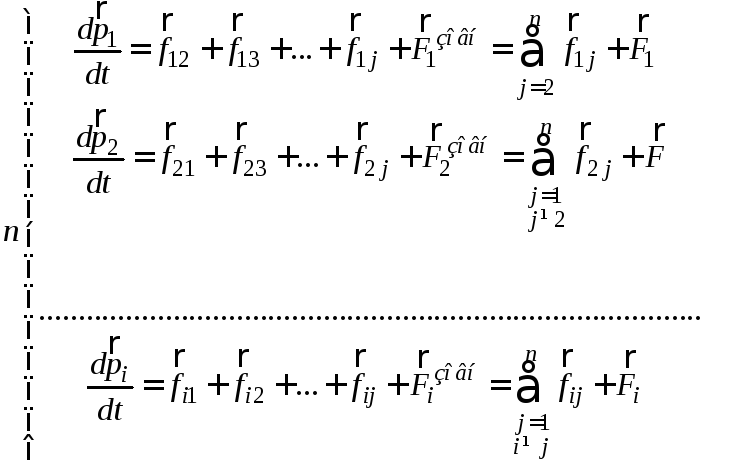(1.56)

Число таких рівнянь рівне кількості матеріальних точок (n), що входять до системи. Розв’язання даної системи із врахуванням початкових умов для кожної матеріальної точки дозволяє описати рух системи в цілому. Однак такий спосіб опису руху системи матеріальних точок виявляється надзвичайно громіздким, оскільки вимагає розв’язання великої кількості диференціальних рівнянь.

Зручніше описати рух системи матеріальних точок з допомогою одного рівняння, яке можна отримати, якщо скласти почленно праві та ліві частини системи рівнянь (1.57):

(1.57)

Згідно третього закону Ньютона , тому. Тоді рівняння (1.57) спроститься до виду:

(1.58)

Враховуючи, що похідна від суми похідних рівна сумі похідних від кожної величини, що входить до суми, рівняння (1.58) можна перетворити до наступного вигляду:

, або (1.59)

де величина 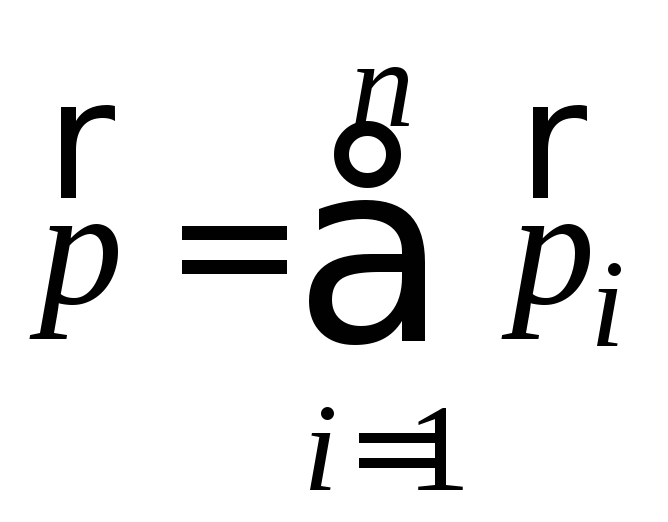називається імпульсом системиn матеріальних точок, – векторна сума усіх зовнішніх сил, прикладених до усіх матеріальних точок системи.