
- •Елементи кінематики
- •1.1.1.Векторні характеристикимеханічного руху– переміщення, шлях, швидкіст та прискорення
- •1.1.2. Рух точки по колу, кутова швидкість і кутове прискорення
- •1.1.3. Зв’язок кутових та лінійних величин
- •1.1.4. Плоскопаралельний рух
- •1.2. Динаміка точки та системи матеріальних точок
- •1.2.1. Закони Ньютона
- •1.2.2. Принцип відносності Галілея
- •1.2.3. Закон динаміки системи матеріальних точок
- •1.2.4. Закон збереження імпульсу
- •1.2.5. Центр мас (інерції) системи матеріальних точок. Теорема про рух центру мас
- •1.2.6. Рух тіл змінної маси
- •1.2.7. Сили інерції. Рух у неінерціальних системах відліку
- •1.2.8. Еквівалентність сил інерції і сил тяжіння
- •1.3. Динаміка обертального руху
- •1.3.1. Момент сили та момент імпульсу
- •1.3.2. Рівняння моментів
- •1.3.3. Рівняння моменту імпульсу для обертання навколо нерухомої осі. Момент інерції
- •1.3.4.Приклади на закон збереження моменту імпульсу
- •1.3.5. Момент інерції. Теорема Гюйгенса-Штейнера
- •1.3.6. Вільні осі обертання. Уявлення про гіроскопи
- •1.3.7. Умови рівноваги твердого тіла.
- •1.4. Закон збереження енергії
- •1.4.1. Енергія, робота та потужність
- •1.4.2. Кінетична енергія поступального та обертального рухів
- •1.4.3. Консервативні сили. Потенціальна енергія
- •1.4.4. Енергія пружно деформованого тіла
- •1.4.5. Потенціальна енергія матеріальної точки у гравітаційному полі та в однорідному полі тяжіння
- •1.4.6. Закон збереження енергії у механіці
- •1.4.7. Пружний та непружний удари тіл та частинок
- •1.5. Всесвітнє тяжіння
- •1.6. Елементи механіки суцільних середовищ
- •1.6.1. Деформація розтягу (стиску)
- •1.6.2. Деформація зсуву
- •1.6.3. Деформація кручення
- •1.6.4. Деформація згину
- •1.6.5. Енергія пружної деформації
- •1.6.6. Аеро- та гідродинаміка
- •1.6.7. Сили в’язкого тертя
- •1.6.8. Види течії в’язкої рідини
- •1.6.9. Рух твердих тіл у рідинах та газах
- •1.7. Елементи спеціальної теорії відносності
Елементи кінематики
Найпростішою формою руху матерії є механічних рух, що полягає в переміщенні тіл чи їх частин одна відносно іншої у просторі із часом.
Механіка – це розділ фізики, що вивчає закономірності механічного руху тіл. При цьому під механічною дією розуміють таку взаємодію з боку інших тіл, яка призводить до зміни стану механічного руху даного тіла або до його деформації.
Розвиток механіки, як науки починається з III ст. до н. е., коли древньогрецький вчений Архімед (287—212 до н. е.) сформулював закон рівноваги важеля і закони рівноваги плаваючих тіл. Основні закони механіки встановлені італійським фізиком і астрономом Г. Галілеєм (1564 – 1642) і остаточно сформульовані англійським ученим І. Ньютоном (1643 – 1727), тому механіку макроскопічних тіл, що рухаються з малими швидкостями (в порівнянні із швидкістю світла у вакуумі c = 3∙108 м/с), називають класичною, або ньютонівською механікою. Релятивістська механіка вивчає рух тіл із швидкістю, що наближається до швидкості світла. Вона базується на спеціальній теорії відносності А. Ейнштейна. Механіку мікросвіту – світу атомів, молекул, електронів тощо – вивчає квантова фізика.
Механіка поділяється на три розділи:
Кінематика – це розділ механіки, в якому досліджується механічний рух тіл, не розглядаючи причини, що цей рух зумовлюють.
Динаміка – це розділ механіки, в якому досліджуються причини, які викликають чи змінюють механічний рух тіл.
Статика – це це розділ механіки, в якому досліджуються закони рівноваги системи тіл. Якщо відомі закони руху тіл, то із них можна встановити і закони рівноваги. Тому закони статики окремо від законів динаміки фізика не розглядає.
Для опису механічного руху тіл в залежності від умов конкретної задачі, механіка використовує різні фізичні моделі. Найпростішою моделлю є матеріальна точка – це тіло, що характеризується масою і розмірами якого в даній задачі можна знехтувати. Поняття матеріальної точки – абстрактне, але його введення полегшує розв’язок практичних задач. Наприклад, вивчаючи рух планет по орбітах навколо Сонця, можна прийняти їх за матеріальні точки.
Структура курсу механіки виглядає наступним чином: спочатку вивчають рух однієї матеріальної точки, далі переходять до вивчення руху системи матеріальних точок.
Рух тіл відбувається у просторі і у часі. Тому для опису руху матеріальної точки необхідно знати, в яких місцях простору ця точка знаходилась і в які моменти часу вона проходила те чи інше положення. Положення матеріальної точки визначається по відношенню до якого-небудь іншого, довільно вибраного тіла, що називається тілом відліку. Звичайно із тілом відліку пов’язують деяку систему координат: декартову (рис.1.3, а), циліндричну (рис.1.3, б), сферичну (рис.1.3, в).
С укупність
просторової системи координат, зв’язаної
з тілом відліку, і синхронізованих
годинників називаєтьсясистемою
відліку.
Найчастіше використовується декартова
система координат, тому у майбутньому
для опису руху ми користуватися саме
нею.
укупність
просторової системи координат, зв’язаної
з тілом відліку, і синхронізованих
годинників називаєтьсясистемою
відліку.
Найчастіше використовується декартова
система координат, тому у майбутньому
для опису руху ми користуватися саме
нею.
1.1.1.Векторні характеристикимеханічного руху– переміщення, шлях, швидкіст та прискорення
Розглянемо різні способи визначення положення точки.
Перший - векторний спосіб опису руху.
У
деяких задачах цей спосіб є найбільш
раціональним. За цим способом положення
точки у просторі визначається
радіусом-вектором
![]() ,
проведеним із початку координат до
точки (рис. 1.4,а):
,
проведеним із початку координат до
точки (рис. 1.4,а):
![]() . (1.1)
. (1.1)
Залежність радіус-вектора точки від часу називається кінематичним рівнянням руху. Лінія, яку описує кінець радіус-вектора разом із матеріальною точкою у просторі, називається траєкторією руху. Залежно від форми траєкторії розрізняють прямолінійний та криволінійний рух. Зауважимо, що форма траєкторії руху точки істотно залежить від вибору системи відліку. Наприклад, у системі відліку, пов’язаній із Сонцем, траєкторії руху планет мають форму еліпсів; у системі відліку, пов’язаній із Землею, їхні траєкторії ускладнюються і нагадують петлеподібні рухи. Точка пропелера рухомого літака з погляду пілота перебуває в коловому русі; в системі відліку, пов’язаній з Землею, її траєкторія має гвинтоподібну форму. До вибору системи відліку треба підходити з урахуванням простоти і зручності опису в ній руху матеріальної точки. Сумарна довжина елементів траєкторії, пройдена точкою за заданий проміжок часу, називається шляхом ΔS.
Рух
точки за час
![]() визначаєтьсявектором
переміщення
визначаєтьсявектором
переміщення
![]() (рис. 1.4,а)
Цей вектор чисельно дорівнює довжині
відрізка прямої, що сполучає початкове
і кінцеве положення точки через час
(рис. 1.4,а)
Цей вектор чисельно дорівнює довжині
відрізка прямої, що сполучає початкове
і кінцеве положення точки через час
![]() і визначається як
і визначається як![]() .
У разі кількох послідовних переміщень
точки сумарний вектор переміщення
знаходять за правилом додавання векторів
(рис. 1.4,б).
.
У разі кількох послідовних переміщень
точки сумарний вектор переміщення
знаходять за правилом додавання векторів
(рис. 1.4,б).
Т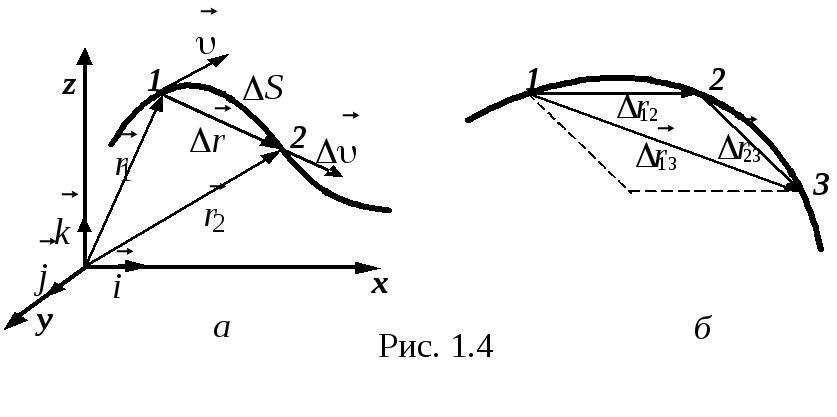 акі
величини, як переміщення, швидкість,
прискорення, сила та інші, що задаються
числовим значенням і напрямом та
додаються за правилом паралелограма,
називаютьсявекторними.
Величини, для визначення яких досить
тільки числового значення, називаються
скалярними
(скалярами). Такими, наприклад, є час,
шлях, маса.
акі
величини, як переміщення, швидкість,
прискорення, сила та інші, що задаються
числовим значенням і напрямом та
додаються за правилом паралелограма,
називаютьсявекторними.
Величини, для визначення яких досить
тільки числового значення, називаються
скалярними
(скалярами). Такими, наприклад, є час,
шлях, маса.
Найважливішою кінематичною характеристикою руху є швидкість.
На практиці в описах рухів часто задовольняються середньою швидкістю, що дорівнює шляху, пройденому за одиницю часу, тобто:
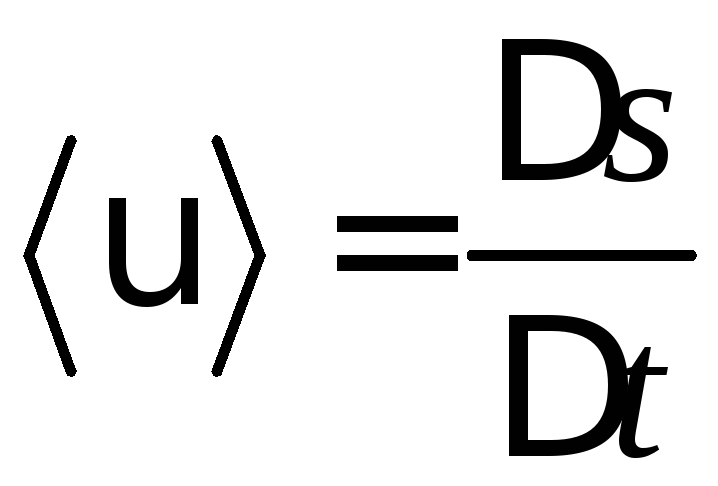 . (1.2)
. (1.2)
Середня швидкість не дає чіткої інформації про рух тіла, а тому для точного опису руху вводиться поняття миттєвої швидкості. Миттєвою швидкістю називається векторна величина, що визначається рівністю
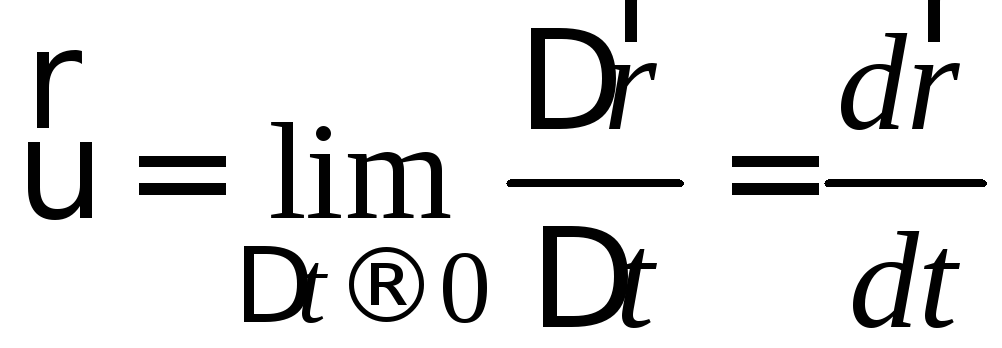 ,
,
![]() (1.3)
(1.3)
Оскільки рух тіла можна уявити як сукупність миттєвих перебувань його в послідовних точках траєкторії, то миттєва швидкість характеризує швидкість тіла в кожний момент часу або в кожній точці його траєкторії. Таким чином, миттєва швидкість – це похідна від радіус-вектора по часу.
Одиницею вимірювання швидкості в СІ є метр за секунду (м/с); на практиці широко користуються кілометром за годину (км/год), у морській справі - вузлом (1 вузол = 1 морська миля/год = 1,853 км/год), у реактивній авіації числом М (1 М ≈ 1200 км/год).
Із
визначення випливає, що швидкість
завжди спрямована по дотичній до
траєкторії (рис.1.4, а).
У міру зменшення t
шлях s
все більше буде наближатися до
![]() ,
тому модуль миттєвої швидкості
,
тому модуль миттєвої швидкості
 (1.4)
(1.4)
де s – шлях, пройдений вздовж траєкторії. Таким чином, модуль миттєвої швидкості рівний першій похідній шляху по часу.
У змінному русі швидкість може змінюватися і за значенням, і за напрямом. Повну зміну швидкості за час Δt знаходять за векторною різницею (рис. 1.4, а):
![]()
Для
оцінювання зміни швидкості в часі
введено фізичну величину, що називається
прискоренням.
У певний момент часу або в заданій точці
траєкторії прискорення є границею
відношення вектора зміни швидкості
![]() до відповідного проміжку часу
до відповідного проміжку часу![]() :
:
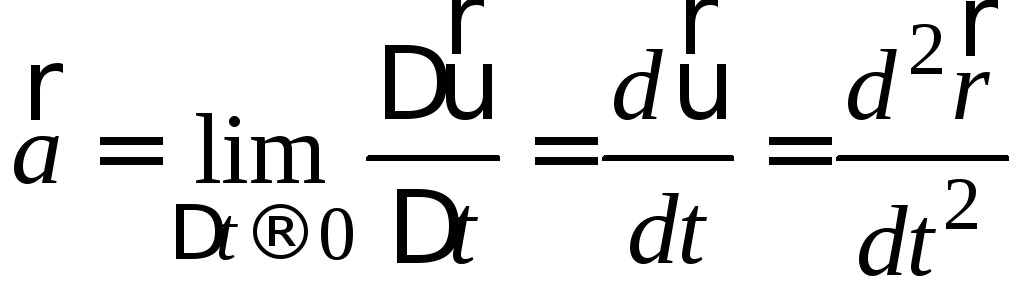 ,
,
![]() . (1.5)
. (1.5)
Таким чином, прискорення є першою похідною від швидкості тіла за часом, або друга похідна від радіус-вектора за часом Про напрямок вектора і його величину мова піде пізніше.
Отже,
знаючи кінематичне рівняння руху, можна
простим диференціюванням за часом
знайти швидкість і прискорення в
будь-який момент часу (так звана пряма
задача кінематики). Навпаки, знаючи
прискорення точки, а також початкові
умови, тобто положення ![]() і швидкість
і швидкість![]() в початковий момент часу
в початковий момент часу![]() ,
можна знайти траєкторію руху точки
,
можна знайти траєкторію руху точки![]() (обернена задача кінематики). Дійсно,
із формул (1.5) і (1.3) випливає, що
(обернена задача кінематики). Дійсно,
із формул (1.5) і (1.3) випливає, що![]() і
і![]() ,
тоді:
,
тоді:
 (1.6)
(1.6)
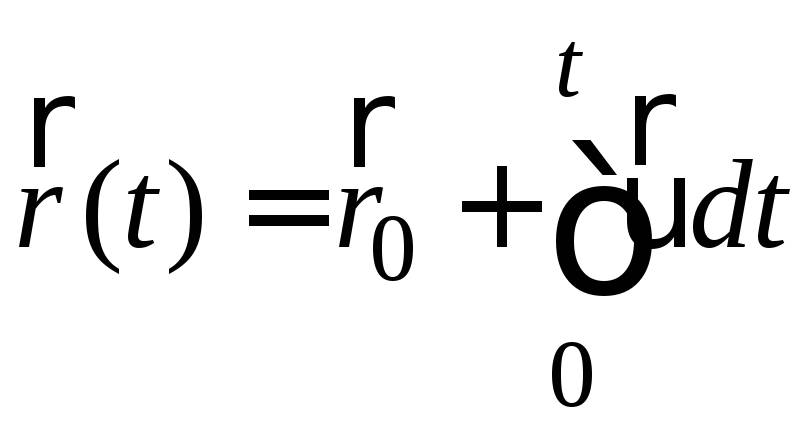 (1.7)
(1.7)
Другий - координатний спосіб опису руху
Якщо з тілом відліку жорстоко пов’язати яку-небудь координатну систему (наприклад, декартову), то положення точки в будь-який момент часу визначається трьома її координатами: x, y, z.
Проектуючи радіус-вектор на координатні осі, отримаємо три залежності координат точки від часу
![]() ;
;
![]() ;
;![]() , (1.8)
, (1.8)
які є кінематичними рівняннями руху в координатній формі. За цими функціями для будь-якого моменту часу можна обчислити координати точки і знайти її положення. Рівняння (1.8) по суті є рівнянням траєкторії у параметричній формі. Щоб знайти рівняння траєкторії у явному вигляді, треба у системі (1.8) виключити час (тобто знайти зв’язок між координатами в довільний момент часу).
Між векторним та координатним способами опису руху точки існує безпосередній зв’язок, а саме:
- числові значення проекцій радіуса-вектора рухомої точки на координатні осі системи з тим самим початком відліку дорівнюють координатам точки, тобто:
![]() ,
,
![]() ,
,
![]() . (1.9)
. (1.9)
І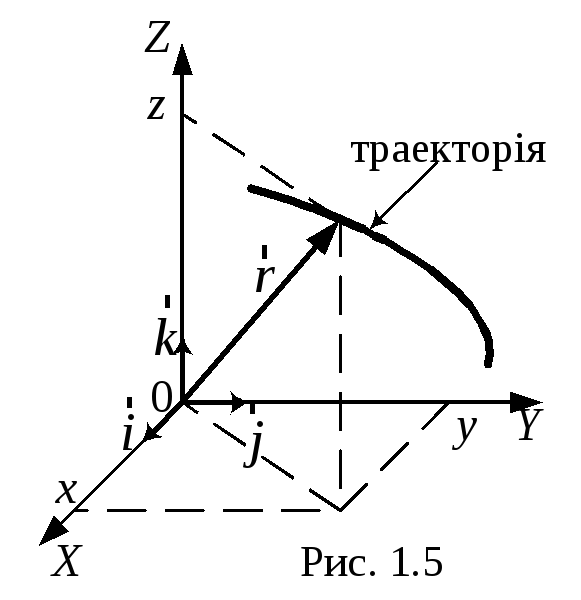 ншими
словами, радіус-вектор можна задати
через координати точки (рис. 1.5), тобто:
ншими
словами, радіус-вектор можна задати
через координати точки (рис. 1.5), тобто:
![]() , (1.10)
, (1.10)
де
![]() –орти
(одиничні вектори, напрямлені вздовж
відповідних координатних осей). Звідси
зараз же випливає принцип
незалежності рухів:
довільний рух точки можна розглядати
як суму незалежних рухів по координатних
осях
x, y, z
;
–орти
(одиничні вектори, напрямлені вздовж
відповідних координатних осей). Звідси
зараз же випливає принцип
незалежності рухів:
довільний рух точки можна розглядати
як суму незалежних рухів по координатних
осях
x, y, z
;
– траєкторією руху точки є годограф радіуса-вектора (крива, яку описує кінець вектора на рисунку 1.4, а). Рівняння (1.8) є рівнянням годографа;
– вектор переміщення виражається через відповідні зміни координат рухомої точки, тобто:
![]() .
.
Як
було сказано вище, при
![]() → 0
вектор переміщення
→ 0
вектор переміщення![]() збігається з відповідним елементом
траєкторії
збігається з відповідним елементом
траєкторії![]() ,
проте для довільного проміжку часу
модуль кінцевого вектора переміщення
і довжина пройденого шляху взагалі
величини різні. Наприклад, модуль
переміщення Землі відносно Сонця як
системи відліку через півроку дорівнює
діаметру орбіти, а через рік – нулю,
тоді як пройдений шлях відповідно
дорівнюватиме половині довжини й довжині
орбіти.
,
проте для довільного проміжку часу
модуль кінцевого вектора переміщення
і довжина пройденого шляху взагалі
величини різні. Наприклад, модуль
переміщення Землі відносно Сонця як
системи відліку через півроку дорівнює
діаметру орбіти, а через рік – нулю,
тоді як пройдений шлях відповідно
дорівнюватиме половині довжини й довжині
орбіти.
Вектори швидкості та прискорення можуть бути вираженими у проекціях на координатні осі:
![]() , (1.11)
, (1.11)
![]() (1.12)
(1.12)
де проекції швидкості і прискорення точки на координатні осі знаходять так:
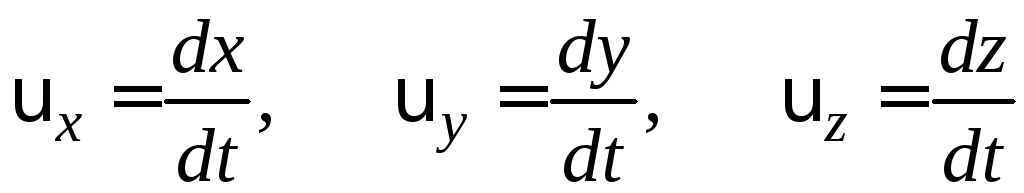 (1.13)
(1.13)
 (1.14)
(1.14)
а модулі векторів знаходять за формулою:
![]() (1.15)
(1.15)
![]() (1.16)
(1.16)
Елементарний пройдений шлях при координатному заданні руху визначається:
![]()
або
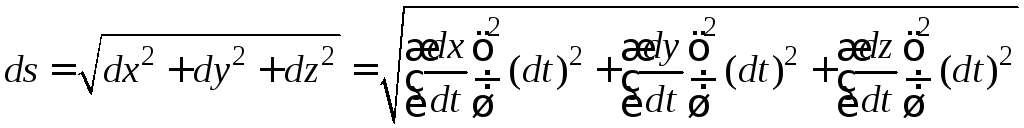 ;
;
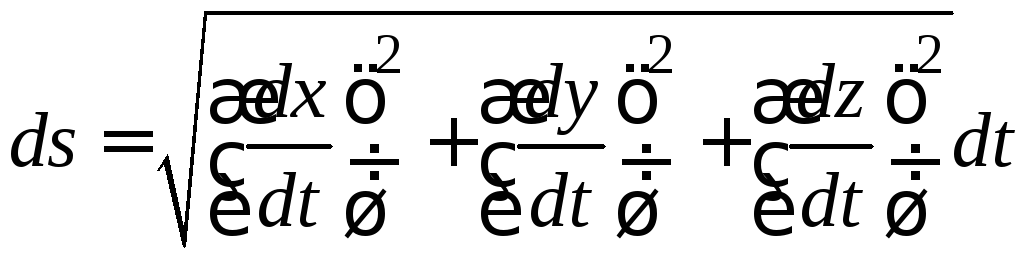 . (1.17)
. (1.17)
Звідси увесь шлях знайдемо шляхом інтегрування:
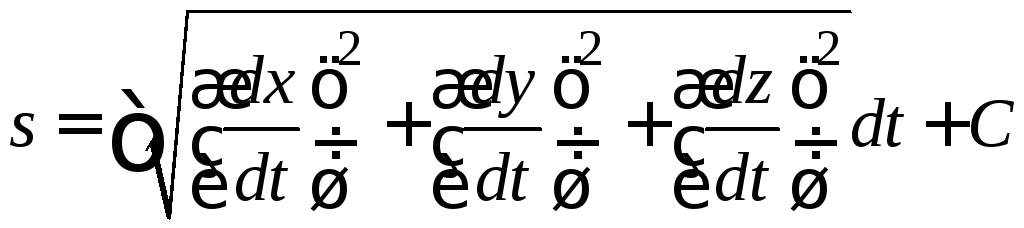 (1.18)
(1.18)
де константа С знаходиться з початкових умов.
Таким
чином, у
кінематиці розв’язують задачі двох
типів:
на знаходження прискорення, коли відомо
функції
![]() ;
;![]() ;
;![]() або
або![]() ,
і на відшукання цих функцій, коли відомі
прискорення.
,
і на відшукання цих функцій, коли відомі
прискорення.
Задачі
першого типу розв’язують методом
диференціювання, другого – методом
інтегрування. Наприклад, для випадку
рівномірно прискореного руху, що
відбувається в напрямі осі Ох,
(![]() )
з виразу
)
з виразу дістаємо:
дістаємо:
![]() ,
,
звідки інтегруванням знаходимо відомі вирази для швидкості та координати:
![]() ;
та
;
та
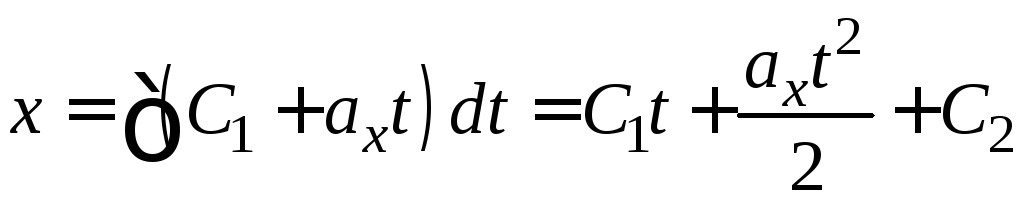 ,
,
де
![]() та
та![]() – сталі інтегрування. Вони визначаються
з початкових умов, а саме: при
– сталі інтегрування. Вони визначаються
з початкових умов, а саме: при![]() = 0
маємо
= 0
маємо![]() та
та![]() .
Тоді рівняння швидкості та координати
буде:
.
Тоді рівняння швидкості та координати
буде:
![]() (1.19)
(1.19)
 (1.20)
(1.20)
Отже,
для розв’язання кінематичних задач,
окрім прискорення, мають бути задані
початкові умови, тобто координати
початкового положення точки (![]() ,
,![]() ,
,![]() )
і початкова швидкість її руху
)
і початкова швидкість її руху![]() (
(![]() ,
,![]() ,
,![]() ).
).
Розглянемо більш детально напрям вектора прискорення.
Як
випливає із (1.5) прискорення – це вектор,
який за напрямом збігається з вектором
![]() при
при![]() → 0.
Зазначимо, що вектор приросту швидкості
→ 0.
Зазначимо, що вектор приросту швидкості![]() може не збігатися з вектором самої
швидкості, тому вектор прискорення
взагалі не збігається з напрямом вектора
швидкості.
може не збігатися з вектором самої
швидкості, тому вектор прискорення
взагалі не збігається з напрямом вектора
швидкості.
У
випадку криволінійного руху швидкість
може змінюватись не лише за величиною,
але й за напрямком (рис. 1.6). Розкладемо
вектор приросту швидкості так:
![]() ,
де доданок
,
де доданок![]() відповідає за зміну вектора швидкості
лише за модулем, а
відповідає за зміну вектора швидкості
лише за модулем, а![]() – лише за напрямком. Тоді повне прискорення
можна записати:
– лише за напрямком. Тоді повне прискорення
можна записати:
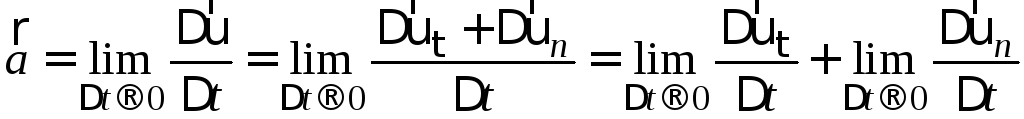 . (1.21)
. (1.21)
П ерший
доданок називаєтьсятангенціальним
прискоренням,
яке характеризує зміну швидкості з
часом за величиною (рис. 1.6) і визначається
за формулою:
ерший
доданок називаєтьсятангенціальним
прискоренням,
яке характеризує зміну швидкості з
часом за величиною (рис. 1.6) і визначається
за формулою:
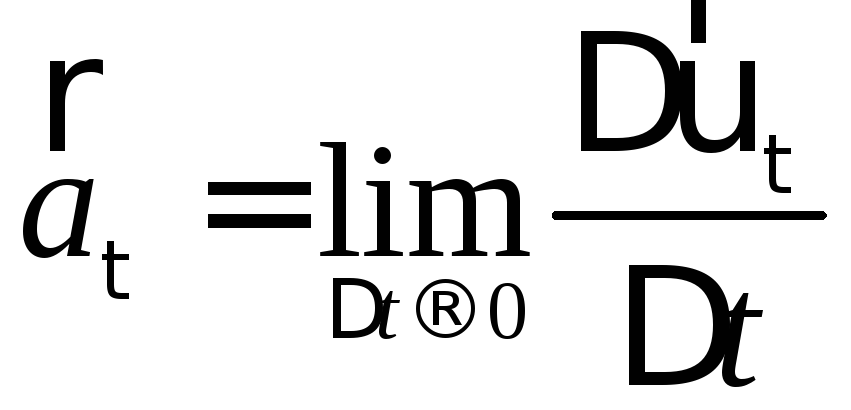 ; (1.22)
; (1.22)
Вектор
![]() можна записати як
можна записати як![]() ,
де
,
де![]() –
орт дотичної до траєкторії, напрямлений
у ту саму сторону, що і вектор швидкості
–
орт дотичної до траєкторії, напрямлений
у ту саму сторону, що і вектор швидкості![]() .
Тоді тангенціальне прискорення:
.
Тоді тангенціальне прискорення:
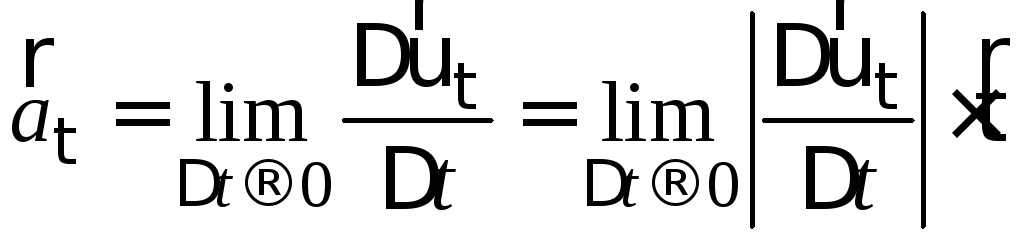 . (1.23)
. (1.23)
Модуль тангенціального прискорення визначається:
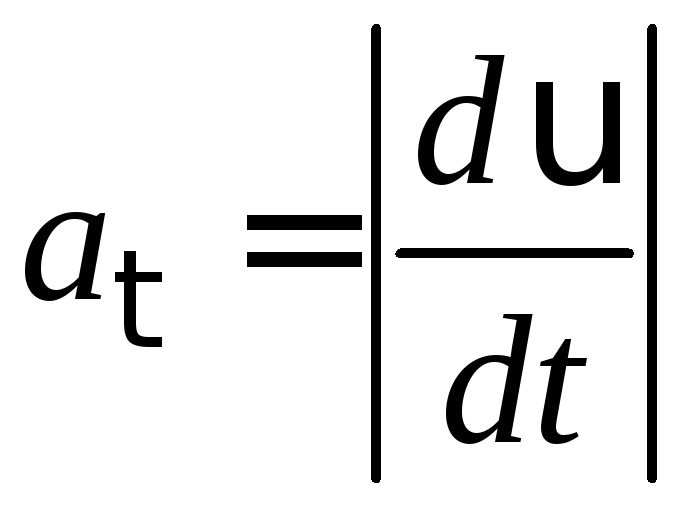 (1.24)
(1.24)
Якщо
 (швидкість зростає за величиною), то
вектор
(швидкість зростає за величиною), то
вектор![]() напрямлений уздовж дотичної у то ж
сторону, що і швидкість
напрямлений уздовж дотичної у то ж
сторону, що і швидкість![]() ,
тобто
,
тобто![]() Якщо ж
Якщо ж (швидкість із плином часу зменшується),
вектори
(швидкість із плином часу зменшується),
вектори![]() та
та![]() напрямлені у протилежні сторони, тобто
напрямлені у протилежні сторони, тобто![]() .
При рівномірному русі
.
При рівномірному русі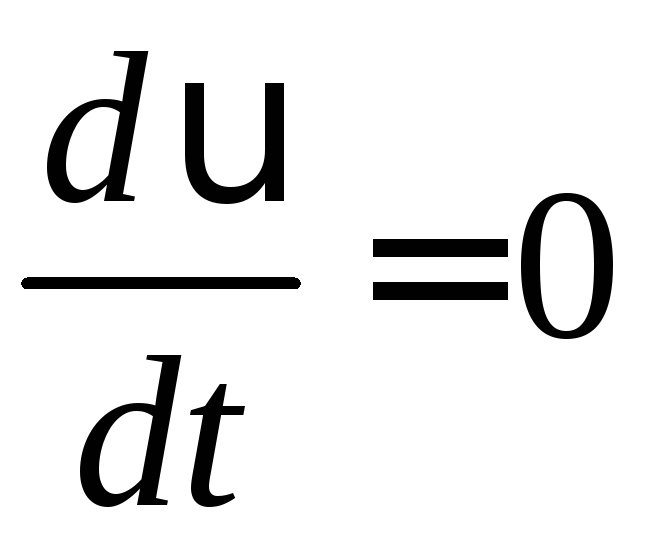 ,
і отже тангенціального прискорення
немає.
,
і отже тангенціального прискорення
немає.
Другий доданок у формулі (1.21) називається нормальним прискоренням, яке характеризує зміну швидкості за напрямком (рис. 1.6) і визначається за формулою:
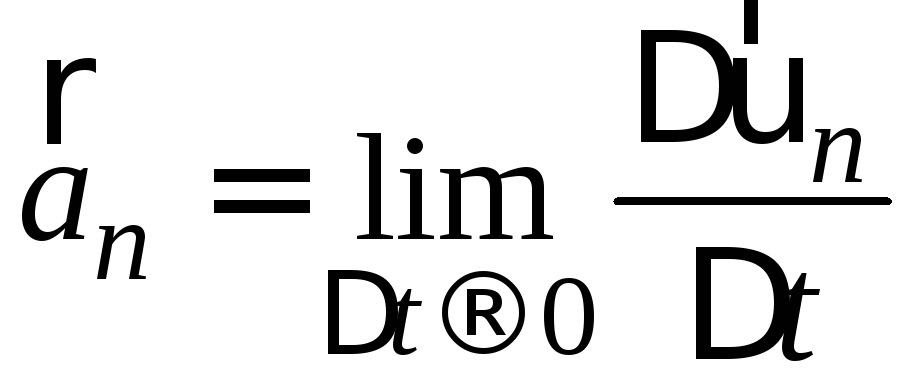 . (1.25)
. (1.25)
Знайдемо модуль
нормального прискорення
![]() .
Як видно з рисунку 1.6
.
Як видно з рисунку 1.6![]() (де
(де![]() ).
Довжина дугиABдорівноє:
).
Довжина дугиABдорівноє:![]() .
Тоді
.
Тоді ,
де
,
де![]() – радіус кривизни траєкторії. У граничному
випадку, коли
– радіус кривизни траєкторії. У граничному
випадку, коли![]() ,
т.Внаближається до т.А.
Звідси:
,
т.Внаближається до т.А.
Звідси:

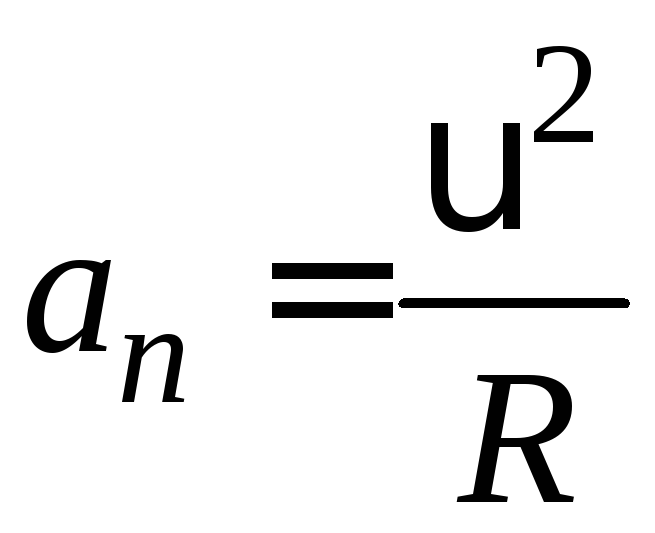 (1.26)
(1.26)
Формула (1.26) визначає модуль нормального прискорення.
Встановимо
напрям вектора
![]() .
Як видно з рисунку 1.6, при
.
Як видно з рисунку 1.6, при![]() .
Тоді з рівнобедреного ΔАСD
слідує, що
.
Тоді з рівнобедреного ΔАСD
слідує, що
![]() АСD=
АСD=![]() АDС ≈ 0.
Таким чином вектор
АDС ≈ 0.
Таким чином вектор
![]() перпендикулярний до швидкості, а отже
–напрямлений
до центра кривизни траєкторії
в даній точці.
перпендикулярний до швидкості, а отже
–напрямлений
до центра кривизни траєкторії
в даній точці.
Повне
прискорення
![]() є векторною сумою тангенціального і
нормального прискорень:
є векторною сумою тангенціального і
нормального прискорень:
![]() (1.27)
(1.27)
З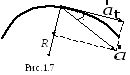 наючи
тангенціальне та нормальне прискорення,
можна знайти модуль і напрямповного
прискорення
в заданій точці траєкторії за теоремою
Піфагора,
оскільки кут між векторами
наючи
тангенціальне та нормальне прискорення,
можна знайти модуль і напрямповного
прискорення
в заданій точці траєкторії за теоремою
Піфагора,
оскільки кут між векторами
![]() та
та![]() завжди 90о
(рис. 1.7):
завжди 90о
(рис. 1.7):
![]() ;
; 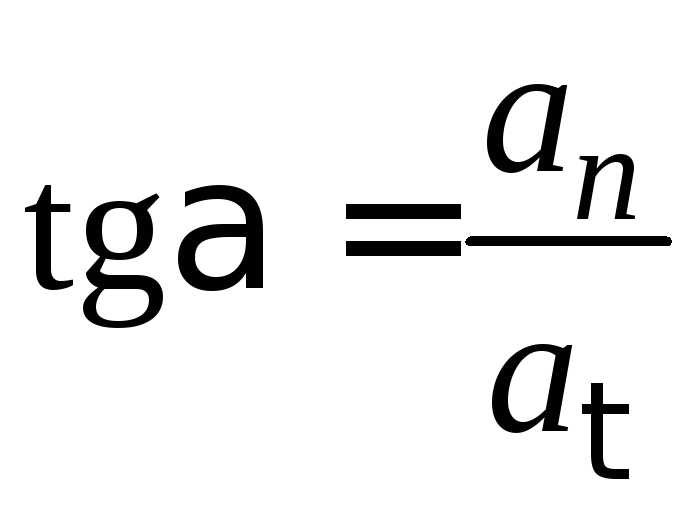 . (1.28)
. (1.28)
Тангенціальне і нормальне прискорення можуть бути використані для класифікації різних рухів, наприклад:
1)
![]() = const
– рівнозмінний рух;
= const
– рівнозмінний рух;
2)
![]() – рівномірний криволінійний рух;
– рівномірний криволінійний рух;
3)
![]() ,
,![]() = const
– рівномірний рух по колу і тощо.
= const
– рівномірний рух по колу і тощо.
