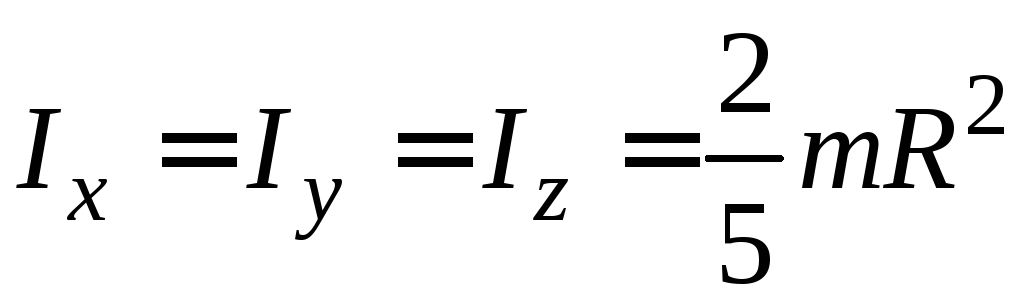1.3.5. Момент інерції. Теорема Гюйгенса-Штейнера

В теоретичній механіці даний момент інерції часто називають осьовим з тим, щоб уникнути плутанини із так званим геометричним моментом інерції, що вивчається в будівельній механіці та в опорі матеріалів. Геометричний момент інерції не пов'язаний з рухом матеріалу, він лише відображає ступінь жорсткості перерізу. Використовується для обчислення радіуса інерції, прогину балки різного поперечного перерізу.

Навпаки,осьовий момент інерції є мірою інертності тіла в обертальному русі так, як і маса характеризує інерційні властивості тіла в поступальному русі. Цю властивість, наприклад, враховують при проектуванні двигуна автомобіля. Так, для регулювання нерівномірності обертання колінчастого вала двигуна автомобіля використовується маховик, що виготовляється у вигляді масивного зубчастого диска. Маховик в машині (рис. 1.37) виконує роль акумулятора кінетичної енергії. При розгоні частина позитивної роботи зовнішніх сил витрачається на збільшення кінетичної енергії маховика і швидкість, до якої розганяється система стає менша, при гальмуванні маховик віддає запасену енергію назад в систему і величина зниження швидкості машини зменшується.

Із визначення (1.94):

видно, що момент інерції є величина адитивна. Тобто, момент інерції тіла рівний сумі моментів інерції його частин. Розглянемо однорідне тіло. Розподіл маси у межах такого тіла можна охарактеризувати густиною ρ, що є однаковою в усіх точках тіла. Тоді елементарна маса дорівнює Звідси момент інерції:

(1.98)

В граничному випадку при нескінченному розбитті тіла на елементарні маси задача знаходження моменту зводиться до інтегрування:

(1.99)

Тут інтегрування здійснюється по всьому об’єму тіла.

Як приклад, розрахуємо момент інерції однорідного суцільного диску радіусом R та товщиною h відносно осі (z), що проходить через його центр (рис. 1.38). Для цього розіб’ємо диск на безкінечно тонкі кільця товщиною dr та радіусом r. Об’єм такого кільця рівний:

Із врахуванням однорідності диску (ρ = const) та рівності (1.99) маємо:

.

Ввівши масу диску як , отримаємо кінцевий вираз для моменту інерції суцільного однорідного диску:

(1.100)

Моменти інерції тіл іншої геометричної форми відносно відповідних осей обертання наведені в таблиці 1.2:

Таблиця 1.2

Фігура або тіло	Осьові моменти інерції
Ідеально тонкий стрижень
Прямокутний паралелепіпед
Суцільний циліндр, суцільний диск
Труба, обруч
Куля
Сфера	при
Прямий коловий конус

Однак, якщо тіло має складну форму і до того ж неоднорідне, його момент інерції простіше виміряти, аніж знайти. У фізиці існують чисельні способи вимірювання моменту інерції, серед яких для прикладу розглянемо два:

1. Визначення моментів інерції тіл обертання з використанням диференціального рівняння обертання.

Досліджуване тіло закріплюється на горизонтальній осіх, що співпадає з його віссю симетрії, і приводиться у рух навколо неї з допомогою вантажу Р, закріпленого на нитці, що намотана на досліджуване тіло (рис. 1.39), при цьому вимірюється час t опускання вантажу на висоту h. Для виключення впливу тертя в точках кріплення тіла на осі х дослід виконується декілька разів при різних значеннях ваги вантажу Р.

При двох дослідах з вантажами Р₁ і Р₂ момент інерції визначається:

2. Експериментальне визначення моментів інерції тіл з допомогою вивчення коливань фізичного маятника.

Щоб знайти момент інерції тіла масою m (рис. 1.40) відносно заданої осі х (що не проходить через центр мас), його потрібно підвісити на цій осі і виміряти два параметри: період коливань Т і відстань l від осі обертання до центру тяжіння. Момент інерції відносно осі визначається за формулою:

Якщо момент інерціїІ_С відносно осі, яка проходить через центр мас, відомий, то можна легко обчислити момент інерції відносно будь-якої паралельної осі О, яка проходить на відстані d від центру мас (рис. 1.41). Як видно з рисунка, відстані довільної точки твердого тіла m_i від обох осей дорівнюють відповідно r_i і r_i + d.

Тому:

(1.101)

Перший доданок визначає момент інерції тіла відносно осі, що проходить через центр мас (т.С): .

Другий доданок в отриманому виразі перетворюється на нуль в силу того, що d = const і (r_C – відстань від осі С до центру мас).

Тоді рівняння (1.101) набуде вигляду:

(1.102)

Співвідношення (1.102) називається теоремою Гюйгенса-Штейнера: момент інерції І тіла відносно довільної осі рівний сумі моменту інерції І_С тіла відносно осі, паралельній даній, що проходить через центр мас тіла, і добутку маси тіла на квадрат відстані між цими осями: