1.6.1. Деформація розтягу (стиску)

Звернімося до досліду. Закріпимо один кінець гумового шнура завдовжкиі потягнемо за інший кінець з постійною силою. Шнур прийде в нове положення рівноваги з довжиною(рис. 1.65). Таку найпростішу деформацію можна охарактеризувати відносним видовженням:

, (1.154)

при цьому видовженню відповідає ε > 0, а стиску – ε < 0.

Відмітимо також, що при розтягу тіла його поперечні розмір d зменшується до величини d₁. Такий поперечний стиск характеризується параметром

(1.155)

Дослідним шляхом встановлено, що відношення до приблизно однакове для різних деформацій одного і того ж матеріалу. Тому у теорії пружності матеріал характеризується коефіцієнтом Пуассона:

. (1.156)

Числове значення коефіцієнта Пуассона лежить у межах: 0 < μ ≤ 1/2.

Для ізотропних матеріалів, що мають однакові механічні властивості по усім напрямкам, 1/4 < μ ≤ 1/3, зокрема, для металів μ = 3/10. Для гуми (продукту вулканізації каучуку) внаслідок практичної нестискуваності коефіцієнт Пуассона μ = 1/2. Для пористих матеріалів (наприклад, коркової винної пробки) μ ≈ 0. У той же час невеликого значення цієї величини у пробки виявляється достатньо, щоб більш-менш легко вийняти пробку штопором: розтягуючись, вона трохи стискається. До речі, саме через це штопор не повинен бути надто жорстким: хороший штопор пружинить, розтягується і разом з тим розтягує пробку по всій її довжині. Пробка із-за цього по всій довжині стає трохи тоншою, що і допомагає її витягнути.

Як установив Гук, при послідовному зростанні навантаження на початку деформації розвиваються рівномірно по довжині стрижня і зростають пропорційно навантаженню, тобто

(1.157)

Величина називається нормальною механічною напругою у торцевому перерізі стрижня. Співвідношення (1.157) виражає закон Гука для деформації розтягу (чи стиску). Коефіцієнт Е називається модулем пружності (або модулем Юнга). Одиницею вимірювання модуля Юнга є паскаль: [E] = Н/м²=Па. Фізичний зміст модуля Юнга: модуль Юнга дорівнює такій нормальній напрузі, яку необхідно прикласти, щоб тіло розтягнути удвічі (тобто, щоб відносне видовження стало рівне одиниці), якщо б такі великі деформації були б можливі. Насправді, вже при значно менших деформаціях відбувається руйнування тіла.

Модуль Юнга Е та коефіцієнт Пуассона μ повністю характеризують пружні властивості ізотропного матеріалу. Усі інші пружні постійні можуть бути виражені через Е та μ. Зокрема, модуль всебічного стиску К (що характеризує об’ємний стиск як: , де р – тиск) виражається через Е та μ співвідношенням:

. (1.158)

Модуль зсуву G (див. нижче його означення) виражається через Е та співвідношенням:

(1.159)

Дослід показує, що закон (1.157) виконується лише в певному інтервалі напруг. Якщо розтягувати стрижень, послідовно збільшуючи від нуля прикладену до нього силу, то щоразу після зняття навантаження, деформація зникає. Однак, при деякій напрузі σ ≥ σ_пр з’являється залишкове видовження. Ця напруга σ_пр називається межею пружності.

Н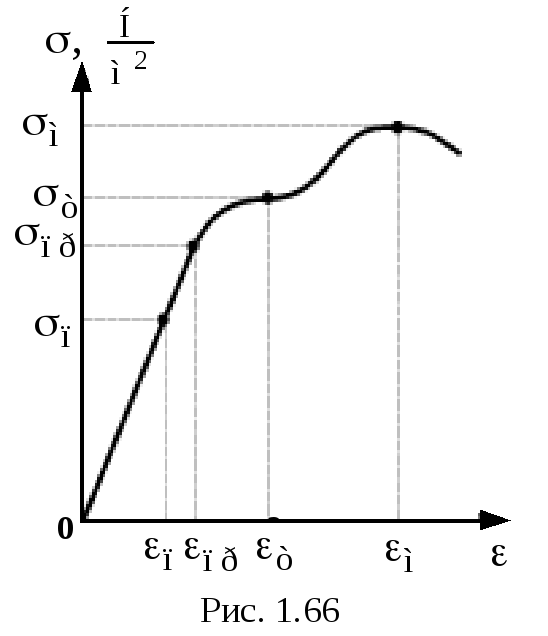а рисунку 1.66 зображена залежність деформації від напруги, що називаєтьсядіаграмою розтягу. Необхідно відмітити, що закон Гука виконується лише в області пружності – області пропорційності, коли 0 ≤ σ ≤ σ_п, де σ_п – межа пропорційності.

При зростанні навантаження спостерігається явище текучості, тобто зростання довжини зразка при постійному навантаженні , що називається межею текучості. Відмітимо, що течія матеріалу відбувається рівномірно по усій довжині стрижня. За межами області текучості подальше видовження стрижня супроводжується зростанням . Однак деформації уже будуть розподілені неоднаково по довжині стрижня (рис. 1.67) – у деякому місці з’являється шийка. При напрузі σ_м, що називається межею міцності, у цьому послабленому перерізі відбувається розрив.

Напругу, яку даний матеріал здатний витримати на практиці, не руйнуючись і не зазнаючи небезпечної деформації, називаютьдопустимою і позначають [σ]. Зазвичай [σ] < σ_пр, і усі розрахунки проводять на основі закону Гука. Щоб забезпечити міцність при усіх обставинах, допустима напруга вибирається як частина межі міцності σ_м, зокрема, для металів [σ] = 0,2∙σ_м, а для дерева [σ] = 0,1∙σ_м. Число, що показує, у скільки разів межа міцності більша за допустиму напругу, називається запасом міцності, тобто

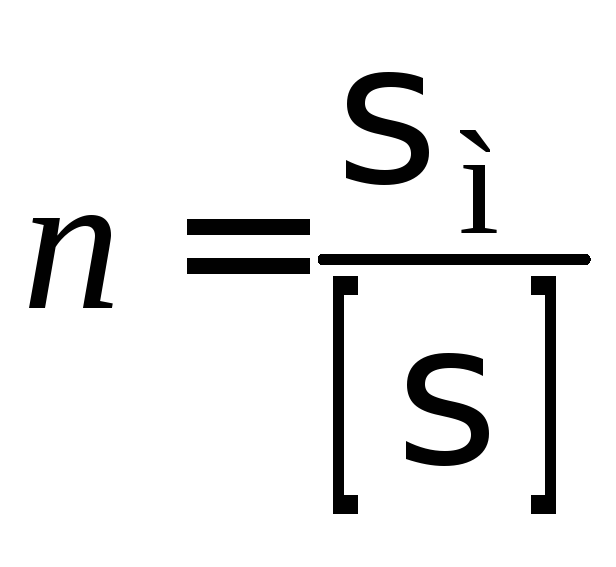(1.160)

Слід зазначити, що найбільші деформації, які може витримати матеріал, визначаються протяжністю області текучості. Якщо область текучості велика, то матеріал називається пластичним. Такий матеріал, як, наприклад, сталь здатний витримати значні навантаження без руйнування. Навпаки, якщо область текучості незначна, то цей матеріал крихкий. Крихкі матеріали, наприклад, чавун, руйнуються при деформаціях ε ≥ ε_пр. Однак у ряді випадків і пластичні деформації можуть руйнуватися при малих деформаціях ε ≈ ε_пр (наприклад, сталь при температурах, нижчих за –45 ^оС).