1.4.4. Енергія пружно деформованого тіла

Під дією зовнішньої сили тіло деформується до тих пір, поки сили пружності не зрівноважать зовнішню деформуючу силу:. Згідно закону Гука. Тоді роботу пружної сили можна виразити рівнянням:

Звідси потенціальна енергія:

Прийнявши потенціальну енергію рівну нулю для недеформованого тіла (х₀ = 0, U (х₀)= 0), отримаємо:

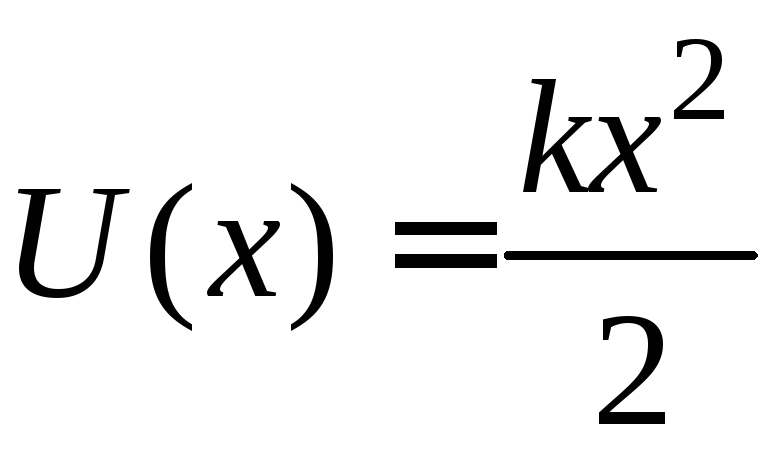(1.132)

1.4.5. Потенціальна енергія матеріальної точки у гравітаційному полі та в однорідному полі тяжіння

За законом всесвітнього тяжіння Ньютона гравітаційна сила притягання двох точкових тіл визначається:

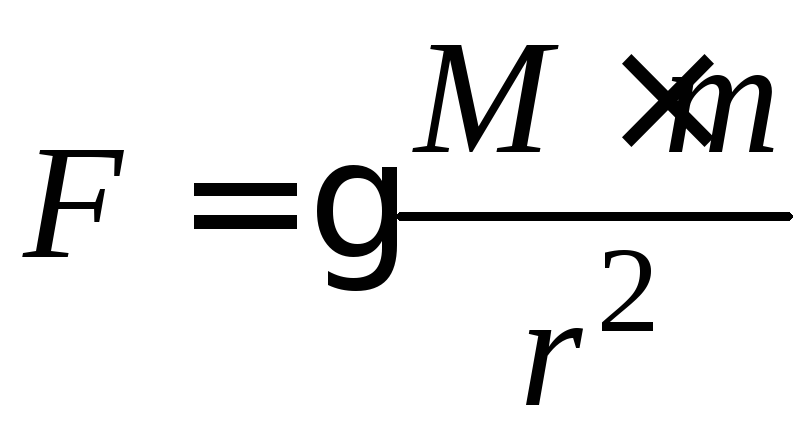
де М – маса тіла, що створює гравітаційне поле, m – маса матеріальної точки, що знаходиться у даному полі.

Сили гравітаційного притягання, як сили центральні, є консервативні. Для них має зміст говорити про потенціальну енергію. Тому:

,

Тоді: .

Приймемо потенціальну енергію взаємодії на нескінченності рівною нулю (U(r_∞)=0). Тоді

(1.133)

Як видно із співвідношення (4.26) потенціальна енергія тіла у полі гравітаційного притягання від’ємна. Але це не є лише властивістю сил притягання – усяким потенціальним силам притягання відповідає від’ємна енергія, оскільки для подолання таких сил частинка витрачає свою кінетичну енергію.

Якщо тіло, що знаходиться на висоті h, упаде на нульовий рівень (тобто рівень, для якого h = 0), то сила тяжіння виконає роботу A = mgh. Тому на висоті h тіло має потенціальну енергію U = mgh + C. За нульовий можна прийняти довільний рівень, наприклад, рівень підлоги, моря тощо. Постійна C рівна потенціальній енергії на нульовому рівні. Покладаючи її рівною нулю, отримаємо:

(1.134)

1.4.6. Закон збереження енергії у механіці

Розглянемо, як змінюються кінетична і потенціальна енергії будь-якої ізольованої системи, в якій діють лише консервативні сили. Нехай в результаті дії цих сил система перейшла із положення (1) в положення (2). Роботу, виконану консервативними силами можна визначити із рівняння (1.124): . Та ж робота може бути виражена через приріст кінетичної енергії (рівняння (1.114)): . Прирівнюючи рівності (1.124) та (1.114) отримаємо:

Сума кінетичної і потенціальної енергії називається повною механічною енергією Е. Таким чином, Е₁ = Е₂. Або

(1.135)

Рівняння (1.135) виражає закон збереження енергії: в системі з одними лише консервативними силами повна механічна енергія залишається незмінною.

Кінетична енергія при цьому може перетворюватися в потенціальну в еквівалентних кількостях і навпаки. Оскільки кінетична енергія за визначенням не може бути від’ємною, то це означає, що потенціальна енергія менша чи рівна повній механічній енергії.

Якщо в замкнутій системі, окрім консервативних сил, діють також неконсервативні, дисипативні сили (сили тертя, опору), то повна механічна енергія системи не зберігається. Дійсно, робота усіх сил при переході системи із положення (1) в (2) визначатиметься:

Прирівнюючи цей вираз до приросту кінетичної енергії, отримаємо:

або

(1.136)

Сили тертя, як правило, здійснюють негативну роботу. Тому наявність сил тертя в замкнутій системі призводить до зменшення її повної механічної енергії з часом. Дія сил тертя призводить до перетворення механічної енергії в інші немеханічні види енергії.

Згідно теореми Емми Нетер закон збереження енергії випливає із однорідності часу.