
- •Елементи кінематики
- •1.1.1.Векторні характеристикимеханічного руху– переміщення, шлях, швидкіст та прискорення
- •1.1.2. Рух точки по колу, кутова швидкість і кутове прискорення
- •1.1.3. Зв’язок кутових та лінійних величин
- •1.1.4. Плоскопаралельний рух
- •1.2. Динаміка точки та системи матеріальних точок
- •1.2.1. Закони Ньютона
- •1.2.2. Принцип відносності Галілея
- •1.2.3. Закон динаміки системи матеріальних точок
- •1.2.4. Закон збереження імпульсу
- •1.2.5. Центр мас (інерції) системи матеріальних точок. Теорема про рух центру мас
- •1.2.6. Рух тіл змінної маси
- •1.2.7. Сили інерції. Рух у неінерціальних системах відліку
- •1.2.8. Еквівалентність сил інерції і сил тяжіння
- •1.3. Динаміка обертального руху
- •1.3.1. Момент сили та момент імпульсу
- •1.3.2. Рівняння моментів
- •1.3.3. Рівняння моменту імпульсу для обертання навколо нерухомої осі. Момент інерції
- •1.3.4.Приклади на закон збереження моменту імпульсу
- •1.3.5. Момент інерції. Теорема Гюйгенса-Штейнера
- •1.3.6. Вільні осі обертання. Уявлення про гіроскопи
- •1.3.7. Умови рівноваги твердого тіла.
- •1.4. Закон збереження енергії
- •1.4.1. Енергія, робота та потужність
- •1.4.2. Кінетична енергія поступального та обертального рухів
- •1.4.3. Консервативні сили. Потенціальна енергія
- •1.4.4. Енергія пружно деформованого тіла
- •1.4.5. Потенціальна енергія матеріальної точки у гравітаційному полі та в однорідному полі тяжіння
- •1.4.6. Закон збереження енергії у механіці
- •1.4.7. Пружний та непружний удари тіл та частинок
- •1.5. Всесвітнє тяжіння
- •1.6. Елементи механіки суцільних середовищ
- •1.6.1. Деформація розтягу (стиску)
- •1.6.2. Деформація зсуву
- •1.6.3. Деформація кручення
- •1.6.4. Деформація згину
- •1.6.5. Енергія пружної деформації
- •1.6.6. Аеро- та гідродинаміка
- •1.6.7. Сили в’язкого тертя
- •1.6.8. Види течії в’язкої рідини
- •1.6.9. Рух твердих тіл у рідинах та газах
- •1.7. Елементи спеціальної теорії відносності
1.4.3. Консервативні сили. Потенціальна енергія
Якщо
деяка величина в кожній точці простору
має певне значення, то існує поле цієї
фізичної величини. Поле називається
скалярним, якщо дана фізична величина
є скалярною, векторна фізична величина
характеризується векторним полем. Якщо
в кожній точці простору на частинку діє
певна сила, це значить, що частинка
знаходиться в силовому полі. Розрізняють
два види силових полів – поле консервативних
сил і поле неконсервативних
сил. Система тіл називається консервативною,
якщо між тілами системи діють сили, що
залежать лише від відстані між
взаємодіючими тілами. Таким чином, для
поля консервативних сил справедливо
співвідношення:
![]() .
Поле сил, що мають такі властивості,
називаєтьсяцентральним.
Прикладом центральної (консервативної)
сили є сила тяжіння:
.
Поле сил, що мають такі властивості,
називаєтьсяцентральним.
Прикладом центральної (консервативної)
сили є сила тяжіння:

Якщо
в усіх точках поля сили, що діють на
частинку, однакові за величиною і
напрямком (![]() ),
поле називаєтьсяоднорідним.
Поле, що не змінюється з часом, називається
стаціонарним.
),
поле називаєтьсяоднорідним.
Поле, що не змінюється з часом, називається
стаціонарним.
 Для
визначення консервативного силового
поля часто використовують властивості
цих сил. Сила
Для
визначення консервативного силового
поля часто використовують властивості
цих сил. Сила
![]() ,
що діє на матеріальну точку, називається
консервативною, якщо робота
,
що діє на матеріальну точку, називається
консервативною, якщо робота![]() ,
що здійснюється цією силою при переміщенні
тіла із положення (1) в положення (2) не
залежить від того, по якій траєкторії
відбувається дане переміщення (рис. 1.57),
а залежить лише від початкового і
кінцевого положення тіла. Тобто
,
що здійснюється цією силою при переміщенні
тіла із положення (1) в положення (2) не
залежить від того, по якій траєкторії
відбувається дане переміщення (рис. 1.57),
а залежить лише від початкового і
кінцевого положення тіла. Тобто
 (1.120)
(1.120)
Отже, інтеграли в (1.120) не залежать від шляху інтегрування. Із останньої рівності можна отримати вираз для роботи консервативної сили по замкненому шляху:
 (1.121)
(1.121)
Таким чином, робота консервативної сили по переміщенню тіла по замкненій траєкторії L = 1→a→2→b→1 тотожно рівна нулю:
 (1.122)
(1.122)
Інтеграл
в рівнянні (1.122) називається циркуляцією
вектора
![]() .
.
Таким чином, консервативні сили можна визначити двома способами:
як сили, робота яких не залежить від шляху, по якому тіло переходить із одного положення в інше;
як сили, робота яких на будь-якому замкнутому шляху рівна нулю.
Консервативними силами є сили тяжіння, сили пружності, сили електростатичного походження, оскільки їхня робота не залежить від форми шляху. Навпаки, сили тертя та опору не є консервативними. Такі сили називають дисипативними.
Вираз
(1.122) означає, що якщо тіло знаходиться
у потенціальному силовому полі, то
робота сил поля не залежить від форми
траєкторії, а є функцією лише початкового
і кінцевого положення (координати)
тіла, тобто існує однозначна функція
координат
![]() ,
причому:
,
причому:
![]() (1.123)
(1.123)
Функцію
![]() називаютьпотенціальною
енергією.
Знак «−» означає, що, якщо поле здійснює
роботу над тілом, то його енергія
зменшується.
називаютьпотенціальною
енергією.
Знак «−» означає, що, якщо поле здійснює
роботу над тілом, то його енергія
зменшується.
Інтегрування рівняння (1.123) призводить до виразу:
 (1.124)
(1.124)
Таким чином, робота, виконана полем консервативних сил, рівна зміні потенціальної енергії. Величина потенціальної енергії в даній точці поля може бути визначена з точністю до постійної інтегрування, тобто:
![]() (1.125)
(1.125)
Тому практичний зміст має не значення потенціальної енергії в даній точці поля, а різниця потенціальних енергій двох точок поля.
Знайдемо зв’язок сили з потенціальною енергією.
![]() (1.126)
(1.126)
 (1.127)
(1.127)
Вираз:
 (1.128)
(1.128)
означає повний диференціал потенціальної енергії.
Вектор сили визначається:
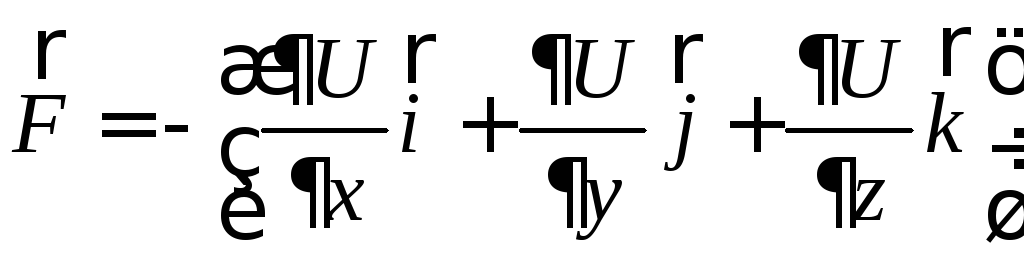 (1.129)
(1.129)
Вектор у дужках в рівнянні (1.129) називається градієнтом скалярної функції U(x, y, z), тобто:
 (1.130)
(1.130)
З врахуванням співвідношення (1.127) рівняння (1.126) можна записати:
![]() (1.131)
(1.131)
З допомогою виразу (1.131) можна визначити силу в будь-якій точці поля, якщо відома потенціальна функція.
