1.4.2. Кінетична енергія поступального та обертального рухів

При переміщенні матеріальної точки масою m під дією сили остання здійснює роботу, а отже енергія рухомої точки зростає на величину роботи сили.

Розрізняють два види механічної енергії: кінетичну і потенціальну енергію. Кінетичною енергією механічної системи називається енергія механічного руху цієї системи.

Зміна кінетичної енергії матеріальної точки відбувається під дією прикладеної до неї сили, яка в свою чергу виконує роботу (див. (1.107)). Оскільки,, то маємо:

(1.111)

Скалярний добуток можна записати як:.

Підставимо останню рівність у рівняння (1.111) та про інтегруємо вздовж траєкторії від точки 1 до точки 2. Маємо:

, (1.112)

де – початкова, а– кінцева швидкості точки. Величина

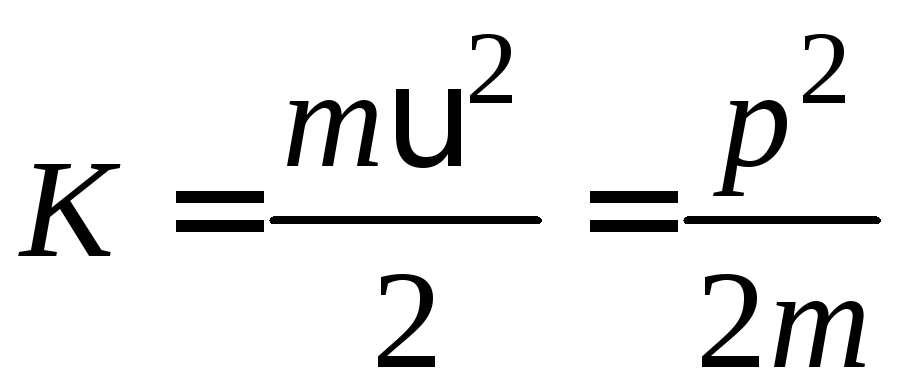(1.113)

називається кінетичною енергією поступального руху матеріальної точки. Отже:

(1.114)

Таким чином, робота сили при переміщенні матеріальної точки рівна приросту кінетичної енергії цієї точки. Із останньої формули слідує, що енергія має таку ж розмірність, що і робота.

Отриманий результат можна узагальнити на випадок довільної системи , що складається з n матеріальних точок:

(1.115)

де – швидкістьі-ї матеріальної точки, m_i – її маса. Зокрема, кінетичну енергію поступального руху твердого тіла, що рухається зі швидкістю υ, можна знайти за формулою (1.113), де m – маса усього тіла.

Під роботою А₁₂ потрібно розуміти суму робіт усіх сил, як внутрішніх, так і зовнішніх, що діють на матеріальні точки системи.

Кінетична енергія залежить від маси тіла і його швидкості, отже, кінетична енергія – функція стану руху тіла чи системи. На відміну від імпульсу кінетична енергія системи не залежить від того, в яких напрямках рухаються її частини. Кінетична енергія залежить від вибору інерціальної системи відліку.

Знайдемо вираз для кінетичної енергії тіла, що обертається навколо нерухомої осі z з частотою ω. Лінійна швидкість елементарної маси m_i дорівнює , деR_i – відстань маси m_i від осі z. Отже, для кінетичної енергії і-ї елементарної маси отримуємо вираз для кінетичної енергії:

. (1.116)

Кінетична енергія тіла складається із кінетичних енергій його частин:

. (1.117)

Сума в правій частині співвідношення (1.117) представляє собою момент інерції тіла І відносно осі обертання. Таким чином, кінетична енергія тіла, що обертається навколо нерухомої осі, рівна

(1.118)

Оскільки кінетична енергія тіла залежить від системи відліку, то для її знаходження зручно користуватися теоремою Кеніга: кінетична енергія системи матеріальних точок (К) рівна сумі кінетичної енергії усієї маси системи, уявно зосередженої в її центрі мас і що рухається разом з ним () та кінетичної енергії цієї ж системи в її русі відносно системи центра мас (): .

Як приклад, використаємо теорему Кеніга для розрахунку кінетичної енергії гусениці трактора відносно землі, що рухається із швидкістю. Маса гусениціm (рис. 1.55). Кінетична енергія центра мас: . Кінетична енергія гусениці відносно центра мас (відносно штрихової системи відліку) рівна, де- швидкість точок гусениці, що дотикаються до землі, відносно системи, зв’язаної із центром мас (системи).

Таким чином,

Для випадку довільного плоского руху (рис. 1.56) кінетична енергія рівна сумі кінетичної енергії поступального руху тіла зі швидкістю центра мас () і кінетичної енергії обертання тіла з кутовою швидкістюнавколо миттєвої осі, що проходить через центр мас (, деІ – момент інерції тіла відносно миттєвої осі):

(1.119)