11. Характеристики пропорционального и интегрирующего звеньев. Пропорциональное звено

В пропорциональном или безынерционном звене выходной сигнал прямо пропорционален входному сигналу: y(t) = k x(t), откуда передаточная функция пропорционального звена: W(p) = k

есть величина постоянная, не зависящая от р. На рис.4.3 приведены примеры пропорциональных (безынерционных) звеньев.

(а)

(б)

(в)

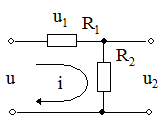
Рис. 4.3 Безынерционные звенья: резистивный делитель (а), инвертирующий усилитель (б), неинвертирующий усилитель (в)

Для схемы на рис. 4.3.а имеем:

u = u₁+ u₂ = i R₁ + i R₂ = i (R₁+R₂), откуда

тогда передаточная функция =.

Для схемы на рис. 4.3.б в соответствии с (4.5) получим: .

В частном случае при получается инвертор, у которого W(p) = -1.

Для схемы на рис. 4.3.в в соответствии с (4.6) имеем: .

Т.к. число , то усилитель на рис.4.3.б называется неинвертирующим.

Интегратор

В интеграторе выходной сигнал связан с входным соотношением: ,

откуда где,- постоянная времени интегратора.

Передаточная функция интегратора: .

Если в схеме на рис.4.2.б вместо включить конденсатор С, а вместо Z включить резистор R (рис. 4.4а) , то в соответствии с (4.5) с учетом (4.4) получим интегратор с инвертированием, у которого, где,= СR - постоянная времени интегратора.

Если перед интегратором включить инвертор, то получится интегратор без инвертирования, у которого .

(а)

(б)

Рис. 4.4 Схемы интегратора (а) и дифференциатора (б)

Основные характеристики интегратора:

ККП ;;;

АЧХ ;

ЛАЧХ ;

ФЧХ ;

ПХ ;

ИХ =.

На рис. 4.5 приведены ЛАЧХ, ЛФЧХ, ПХ и ИХ интегратора.

Рис. 4.5. Графики ЛАЧХ, ЛФЧХ, ПХ и ИХ интегратора

12. Характеристики дифференциатора и инерционного звена первого порядка

На рис. 4.2 приведены две схемы включения операционных усилителей: инвертирующего (а) и неинвертирующего (б).

(а)

(б)

Рис. 4.2 Схемы включения операционных усилителей: инвертирующего (а) и неинвертирующего (б)

Для схемы на рис. 4.2.а передаточная функция определяется по формуле: , (4.5) а для схемы на рис. 4.2.б - по формуле:. (4.6)

Дифференциатор

В дифференциаторе выходной сигнал связан с входным соотношением: ,

откуда , где,- постоянная времени дифференциатора.

Передаточная функция дифференциатора .

Если в схеме на рис. 4.2б вместо включить резистор R, а вместо Z включить конденсатор С (рис. 4.4б), то в соответствии с (4.5) с учетом (4.4) получим дифференциатор с инвертированием

, где- постоянная времени дифференциатора. При необходимости инверсию можно устранить, включив последовательно с дифференциатором инвертор, у которого W(p) = -1. Тогда получим.

Основные характеристики дифференциатора:

ККП ,,.

АЧХ .

ЛАЧХ .

ФЧХ .

ПХ .

ИХ .

На рис. 4.6 приведены ЛАЧХ, ЛФЧХ, ПХ и ИХ дифференциатора.

(а)

(б)

Рис. 4.6. Графики ЛАЧХ, ЛФЧХ, ПХ и ИХ дифференциатора

Инерционное звено

В инерционном или апериодическом звене выходной сигнал связан с входным соотношением

, откуда Y(p) = k X(p) - p T Y(p) , (4.7) где Т - постоянная времени звена.

Передаточная функция инерционного звена следует из (4.7) . (4.8)

Если в схеме на рис. 4.2.а вместо конденсатор С, а вместовключить резистор R (рис. 4.7.а), то в соответствии с приведенными на рис. 4.7.а обозначениями получим

(а)

(б)

Рис. 4.7. Схемы инерционного звена (а) и дифференцирующей цепи (б)

,,.

Тогда .

По определению W(p) = .

После сокращения числителя и знаменателя на рС получим W(p) = , где Т = RC - постоянная времени.

Основные характеристики инерционного звена с передаточной функцией (4.8):

ККП ;;;

АЧХ ;

ЛАЧХ =;

ФЧХ ;

ПХ =;

ИХ .

На рис. 4.8 приведены годограф ККП, ЛАЧХ, ЛФЧХ, ПХ и ИХ инерционного звена, а также кусочно-линейная аппроксимация ЛАЧХ.

Частота называется частотой сопряжения отрезков прямых. До частоты ЛАЧХ идет параллельно оси абсцисс, а выше частотыЛАЧХ имеет наклон -20 дБ/дек. На частотеФЧХ имеет значение.

Рис. 4.8 Графики годографа ККП, ЛАЧХ, ЛФЧХ, ПХ и ИХ инерционного звена